ABC351
我多久没更新这个系列了啊
把格子分成两类，每一类之间的坐标均可互相走到。
然后将这里面的点都旋转 \(45\) 度，于是这个问题就被转换成曼哈顿距离的问题了。
我们可以把 \(x\) 和 \(y\) 拆开计算。
然后我们排个序，求个差分，然后对于每一个区间算贡献即可。
非常简单的树状数组。
我们先对序列排一个序，然后从小到大一次插入每一个数。
在每一次询问时我们都知道有多少个数满足 \(j \le i\) 且 \(a_j \le a_i\) 而且我们知道满足这个条件的所有数的和。
所以我们拿两棵线段树分别维护个数和和即可。
非常恶心的树链剖分。
我们维护每一棵子树的 \(b_x\)，\(b_x\) 表示 \(\Pi\) 轻子树 \(f_x\)。
然后我们维护这个这个点的 \(f_x\)，记作 \(sum\)，并且维护 \(b_x\) 的前缀积 \(mul\)。
于是我们就能够使用一个线段树来维护这两个值。
下面是 push_up 的写法：
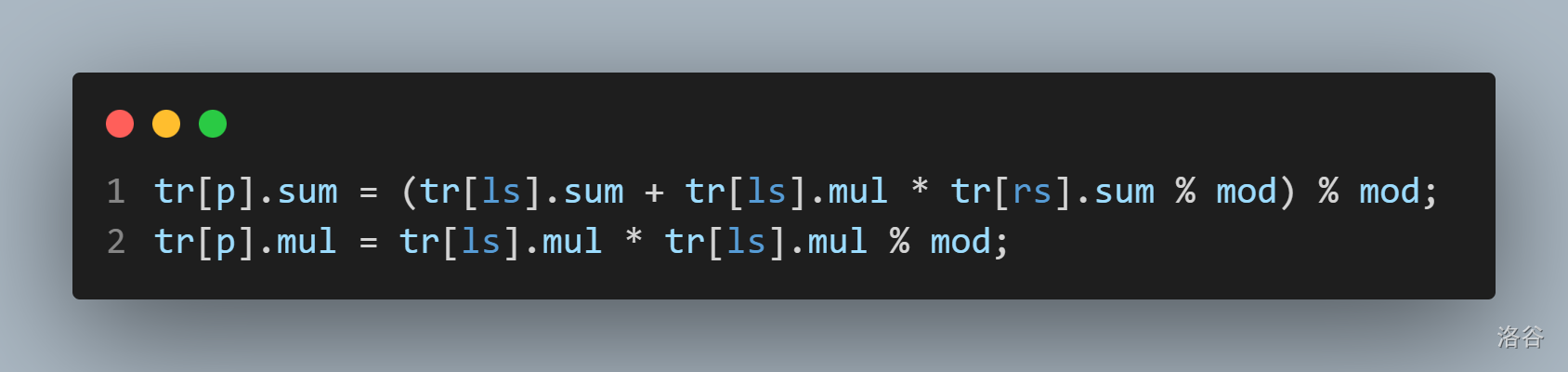
修改的时候直接往上跳，因为我们可以处理每一条链对答案的贡献。
