CF364E
算法1
我会暴力！！！
直接枚举右上角和左下角，然后计算答案，使用前缀和优化后时间复杂度为 \(O(n^4)\)。
算法2
我会分治！！！。
我们知道答案就是左边+右边+两边都有的个数。
左右递归求解即可，所以考虑两边都有的个数。
我们知道满足有 \(k\) 个 \(1\) 的可能为上面有 \(i\) 个点，下面有 \(k - i\) 个点，\(i \in [0,k]\)。于是我们可以考虑维护上面的矩阵有 \(i\) 个点的情况数。
先枚举左右端点，表示我们想要求的矩阵的左右两边。
对于每一个宽度我们会考虑到底有多少个矩阵有 \(i\) 个 \(1\)。于是定义 \(up_{0,i}\) 为在规定左右两边的情况下上边界到 \(mid\) 的矩阵中的 \(1\) 的个数 \(<i\) 的最大值。同理定义 \(up_{1,i}\) 为在规定左右两边的情况下 \(mod\) 到下边界的矩阵中的 \(1\) 的个数 \(<i\) 的最小值。
于是我们就知道上边界到 \(mid\) 组成的矩阵中有 \(i\) 个 \(1\) 的个数为 \(up_{0,i} - up_{0,i + 1}\)。
所以我们可以暴力的去求解这个值，由于左右两边会移动，所以我们的 \(up\) 数组也在变化。假如我们每一次都遍历一遍去 \(up\) 数组，那是肯定会超时的，考虑优化。
我们先来研究当右端点往后一一位后 \(up\) 的变化。在这里我就以 \(up_0\) 为例，\(up_1\) 同理。
1.后面那一列并没有任何 \(1\)
很明显他是不会变的，这应该可以理解吧。所以左端点为 \(i\)，右端点为 \(j\) 对应的 \(up_{0,k}\) 就等于左端点为 \(i\)，右端点为 \(j + 1\) 对应的 \(up_{0,k}\)。
2.后面那一列有 \(1\)
我们可以画个图来感性理解一下。
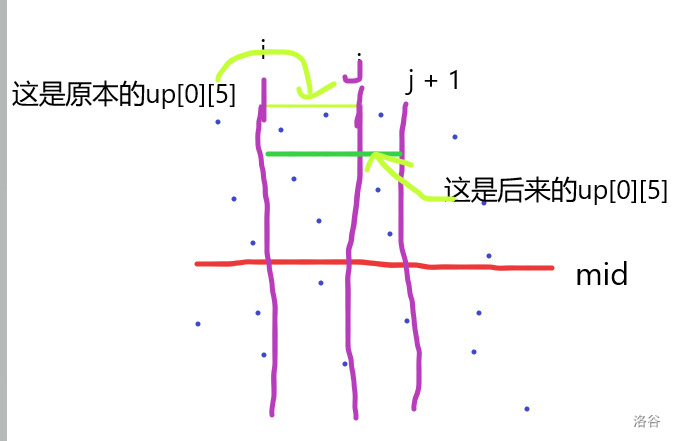
我们发现这个数下降了，但是这个数还有可能是不变的，这个情况就留给读者自己构造。
综上左端点为 \(i\)，右端点为 \(j\) 对应的 \(up_{0,k}\) 小于等于左端点为 \(i\)，右端点为 \(j + 1\) 对应的 \(up_{0,k}\)。
\(up_1\) 也是如此。
所以我们就知道 \(up\) 数组拥有单调性。于是我们就可以像单调队列一样去维护 \(up\) 数组了。
求出 \(up\) 数组后，本题就很简单了，答案就是上面的矩阵有 \(i\) 个点的情况 \(\times\) 下面的矩阵有 \(k - i\) 个点的情况。
二维分治有两种写法，第一种是横着劈一刀，然后竖着劈一刀，还有一种就是每一次都劈两条边中更长的那条长的。
上面讲的 \(up\) 的维护方法是横着劈的，竖着劈同理。
时间复杂度为 \(O(knm \log n)\)。
