莫队
Part -1 前言
本文为莫队学习笔记,如果有错误,请提出,谢谢捏。
Part 0 目录
- 普通莫队
- 1.形式
- 2.算法流程
- 3.小trik
- 4.例题
- 1.小Z的袜子
- 2.AHOI2013作业
- 3.八云蓝自动机 Ⅰ
- 带修莫队
- 1.引入
- 2.过程
- 3.实现
- 回滚莫队
- 1.引入
- 2.只加不减的回滚莫队
- 3.只减不加的回滚莫队
- 4.例题
- 1.历史研究
- little trick --- bitset+莫队
- 1.引入
- 2.例题
- 1.掉进兔子洞
- 树上莫队
- 莫队二离
- 1.前言
- 2.过程 & 例题
- 3.再来一道例题
- 一些例题
Part 1 普通莫队
1.形式
假如说通过区间 \([l,r]\) 的答案可以 \(O(1)\) 求出 \([l - 1,r]\),\([l + 1,r]\),\([l,r - 1]\) 和 \([l,r + 1]\) 的答案那么我们求可以在 \(O(n \sqrt n)\) 的时间内解决问题。
相当于在平面直角坐标系上有 \(n\) 个散点,然后我们用莫队来串起这 \(n\) 个散点。
2.算法流程
先把所有的问题离线下来,然后以 \(l\) 所在的块的编号为第一关键字,以 \(r\) 为第二关键字。
然后求答案即可。放一个移动求答案的代码。
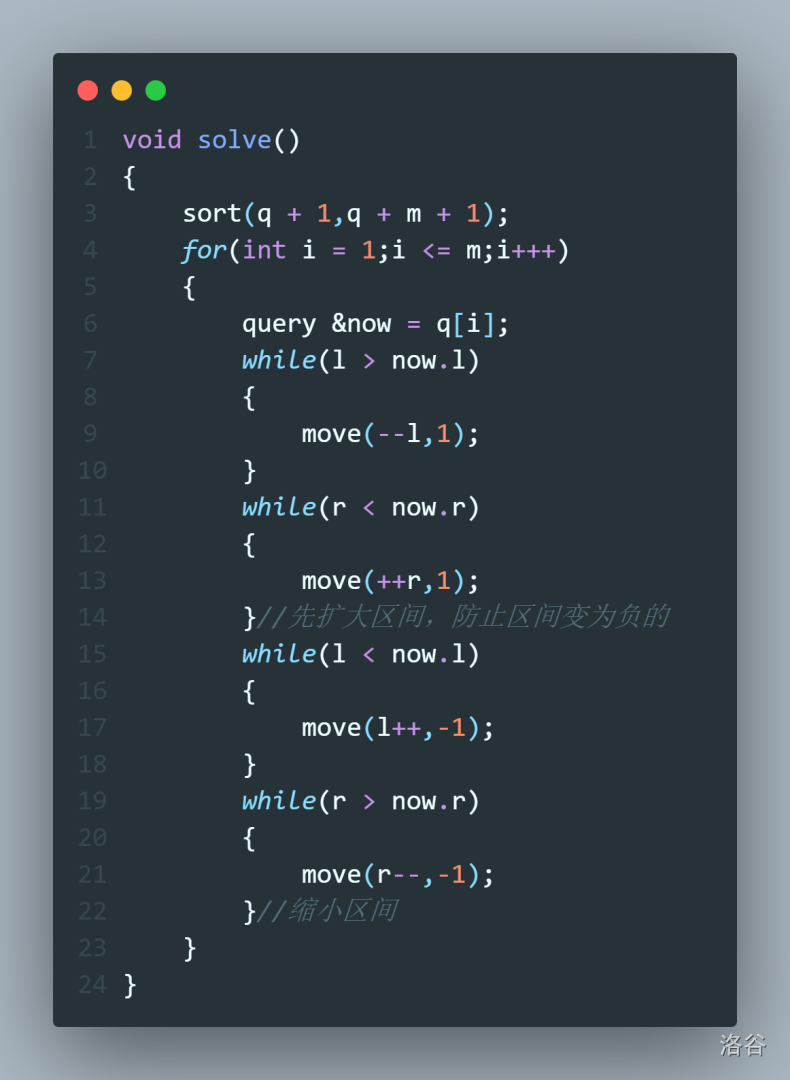
3.小trik
我们知道如果按照 \(l\) 为关键字的话,莫队会走完这一行,然后回到最开头,向上走一格,然后继续走这一行。
但是我们可以直接到尽头时向上走,然后倒退回去,这样这两行只需要两次就可以遍历完。但是不这样就需要四次。
所以我们可以在奇数行的时候按照普通的,否则我们倒着排序。
4.例题
1.小Z的袜子
莫队模板题。
对于 \([l,r]\) 区间取到两个相同颜色的袜子的情况数为 \(\sum^{i\le n}_{i=1} cnt_i \times(cnt_i - 1)\)。总情况数就是 \((r - l + 1) \times (r - l)\)。
然后我们用莫队维护 \(cnt\) 即可。
2.AHOI2013作业
知识点:分块+莫队。
题目大意
在区间 \([l,r]\) 中大小在 \([a,b]\) 中的数有多少个,以及去重后有多少个?
Solution
如果我们直接利用莫队,那我们需要在用一个 BIT 来维护某个值域区间中的数,这样带 \(\log\) 十分容易想到。但是我们要把 \(\log\) 去掉,所以 pass 掉这个算法。
莫队算法的复杂度主要在修改上,其修改复杂度为 \(O(n\sqrt n)\) 可他的询问复杂度仅为 \(O(n)\)。所以我们要一个 \(O(1) - O(\sqrt n)\) 的数据结构。明显,我们可以想到用值域分块来解决这个问题。
所以复杂度即为 \(O(n \sqrt n)\),这样就可以把 \(\log\) 去掉。
3.八云蓝自动机 Ⅰ
首先我们对于操作 \(1\) 转换,我们给 \(k\) 单独再开一个点 \(a_c\),这样我们就可以把操作 \(1\) 转换成操作 \(2\) 了。
对于区间问题,我们考虑使用莫队进行维护。
我们记录当前 \(a\) 的值,\(pos_i\) 表示原来第 \(i\) 个位置的数现在在哪里,\(rev_i\) 维护现在第 \(i\) 个数原来在哪里,和 \(add_i\) 现在第 \(i\) 个位置上查询了多少次。
首先我们先考虑指针 \(r\) 往右移的情况。
- 这个操作是交换
直接交换 \(a_x\) 和 \(a_y\),\(rev_x\) 和 \(rev_y\),\(pos_{rev_x}\) 和 \(pos_{rev_y}\)。
- 这个操作是查询
直接给 \(ans\) 加上 \(a_x\),然后 \(add_x\) 加 \(1\) 即可。
然后我们考虑指针 \(l\) 往左移的情况。
- 这个操作是交换
我们同样先交换 \(a_x\) 与 \(a_y\),\(rev_{pos_x}\) 和 \(rev_{pos_y}\) 以及 \(pos_x\) 和 \(pos_y\)。
由于这个操作会影响到后面的查询操作,所以这个操作会改变答案。所以在交换后我们需要加上 \((a_{pos_x} - a_{pos_y}) \times (add_{pos_x} - add_{pos_y})\)。
- 这个操作是查询
和上面一样,\(ans\) 加上 \(a_{pos_x}\),\(add_x\) 加上 \(1\)。
剩下两种类似,只需改改符号即可。时间复杂度 \(O(n\sqrt n)\)。
最后要注意本题对 \(2^{32}\) 取模。
Part 2 带修莫队
1.引入
众所周知,莫队是不以直接修改的,但是题目有时候会要求我们修改,比如这道题。
2.过程
由于莫队为离线数据结构,所以我们需要考虑怎么维护这个修改操作。
但是我们可以强行修改,我们可以直接加上一维表示时间。所以就是把询问从 \([l,r]\) 改为 \([l,r,time]\),同时我们可以在时间维上移动。其实就相当于在高维莫队。
这样子的转移依然为 \(O(\sqrt n)\)。
3.实现
查询很简单,所以我们来考虑修改。
我们定义 \(l \le r\),然后我们要修改一个点,假如这个点是从一个经历修改次数为 \(l\) 的询问转移到一个经历修改次数为 \(r\) 的询问上。
但是我们要如何强行加上这个修改呢?
假设修改前位置 \(pos\) 的颜色为 \(a\),修改后为 \(b\),并且莫队已经到了 \([l,r]\)。
-
加上这个修改,有两种情况。第一种加入 \(pos\) 在 \([l,r]\) 中,就是删掉颜色 \(a\),加上颜色 \(b\) 并且把序列中 \(pos\) 改为 \(b\)。否则把序列中 \(pos\) 直接改为 \(b\) 即可。
-
还原这个修改,相当于把 \(pos\) 位置上的 \(b\) 改为 \(a\)。
接下来我们考虑维护查询操作:
我们在 \(l\) 维和 \(r\) 维上正常移动,然后额外在 \(tim\) 维上移动即可。
所以就很容易做出来啦!!
Part 3 回滚莫队
1.引入
有些时候,往莫队加一个数十分简单,可是删去一个数就非常难维护。但是有时候删去一个数非常容易,但是加入一个数就难以维护。
此时我们就要用到回滚莫队。
2.只加不减的回滚莫队
先按照左端点所在的块升序为第一关键字,以右端点升序为第二关键字的方式排序。
对于处理左端点在 \(T\) 位置的区间,先初始化 \([R_T+1,R_T]\) 这个空区间。
假如询问的左右端点在同一个块里,那么直接扫描区间得出答案。
否则呢?
假如询问的右端点大于莫队的右端点,那么不断扩展右端点直至莫队区间的右端点等于询问的右端点。加入左端点和莫队的左端点不在同一个块里,那么不断扩展莫队区间的左端点直至莫队区间的左端点等于询问的左端点,然后直接回答询问。然后撤销左端点的改动,让左端点重新回到 \(R_T + 1\) 的位置。
然后复杂度依然为 \(O(n\sqrt n)\)。
3.只减不加的回滚莫队
先按照左端点所在的块升序为第一关键字,以右端点降序序为第二关键字的排序方法排序。
对于处理左端点在 \(T\) 位置的区间,先初始化 \([L_T,n]\) 这个空区间。
然后和上面做差不多的事情即可,只是把加操作改为减操作。
4.例题
1.历史研究
题目让你求每次回答区间内元素权值乘以元素出现次数的最大值。
加点非常好写,直接开个桶维护个数即可。
但是删除操作不好维护,我们删掉这个点的时候我们并不知道接下来谁是最大值,所以我们使用回滚莫队。
那么回滚莫队中提到的撤销操作具体就是指在桶中减去出现次数,而不管答案是否改变。
little trick --- bitset+莫队
1.引入
bitset 可以用来常规数据结构难以维护的的判定问题。然而莫队却可以常规数据结构难以维护的区间问题。
所以我们可以把两者结合,这样可以同时利用两者的优势。
2.例题
1.Ynoi 2016掉进兔子洞
题目要求三个区间内不同时出现的数的个数,所以答案即为三个区间的长度之和 - 三个区间内同时出现的数的个数。
然后看到 \(a_i \le 10^9\),于是需要离散化,但是本题考的是区间内出现数的个数,所以不需要使用 unique,直接使用 lower_bound 即可。
既然考到了区间内出现的数的个数,我们可以想到莫队。
对于每一个询问都开一个 bitset,这个 bitset 中的每一位表示这个数是否取过。然后对于每一个小区间,我们也开一个 bitset,这个 bitset 表示当前数是否取过,所以最后需要删除的数的个数就是三个 bitset 的交集。
但是注意到 \(n,m\le 10^5\),虽然 bitset 可以开很大的范围,但是开不了 \(10^5 \times 10^5\) 的空间,于是我们把询问分成几次来计算即可。大约开 \(2 \times 10^ 4\) 就行了。
Part 4 树上莫队
形式1
1.过程
既然莫队一般只能处理序列上的问题,那么我们就直接强行把这整一颗数压成一个序列。
首先我们先遍历这整一颗树,加入我们遇到了 \(u\) 节点,那么我们就 push_back(u),假如我们回退到 \(u\) 节点,那么我们就 push_back(-u)。
然后当我们在挪动指针时
- 加入的值为 \(u\) ->
add(u) - 加入的值为 \(-u\) ->
del(u) - 删除的值为 \(u\) ->
del(u) - 删除的值为 \(-u\) ->
add(u)
这样我们就可以把这棵树变成一个序列了。
2.例题
糖果公园
先把一棵树变为一个括号序列,然后每次添加/删除一个点,这个点的对答案的的贡献是可以在 \(O(1)\) 的时间内获得,即 \(val_c \times w_{cnt_{c+1}}\)。
对于重复的贡献我们直接开一个 vis 数组看这个点需不需要计算。假如 \(vis_u\) 为 \(0\),那么我们就不计算这个点的贡献。每一次操作之后直接让 \(vis_u\) 异或 \(1\) 即可。
所以直接树上莫队解决即可。
还有修改,所以直接加上一维时间为即可。不会带修莫队的可以往前看。
所以就解决了。
形式2
1.引入
上面只是把一棵树拍平,变成一个括号序列里面,这并不是真正莫队上树,那还是在序列上做的。
众所周知,莫队是基于分块的。所以在讲莫队上树时,我们需要了解树分块。
2.树分块
顾民思义,就是在树上分块。
具体要求如下:
-
属于同一块的节点之间的距离不超过给定块的大小
-
每个块中的节点不能太多也不能太少
-
每个节点都要属于一个块
-
编号相邻的块之间的距离不能太大
然后我们用一个 stack 来维护,假如 stack 里面的数的个数大于等于块长,那么这里面的点就成为一个新的块。
3.过程
首先先把整棵树分块。
然后和普通莫队一样,设置左端点和右端点。但是怎么移动呢?
我们可以标记被计入答案的点,让指针直接向目标移动,同时取反路径上的点。
对于两个点的 lca 我们先不计算,等做完所有的点之后我们在此单独计算两个点的 lca 即可。
排序的方法即为按照第一个点的编号排序即可。
4.例题
1.COT2
就是模板题。直接维护颜色数量即可。
注意移动时需要特判 lca。
Part 5 莫队二离
1.前言
这个神秘科技适用于
- 一个区间的贡献和区间的数有关
- 答案可以前缀和算出
二离的复杂度为 \(O(q \times k + q \times \sqrt n)\),其中 \(k\) 为一次转移的复杂度。
2.例题 & 过程
发现 \(k\) 最大为 \(14\),若用普通莫队做需要 \(O(C^k_{14})\) 的复杂度转移,显然普通莫队经受不了。
我们考虑使用莫队二离。
令 \(f(i,[l,r])\) 为 \(a_i\) 对于区间 \([l,r]\) 的贡献。
显然 \(f(i,[l,r]) = f(i,[1,r]) - f(i,[1,l - 1])\)。由于答案从区间 \([l,r]\) 转移到区间 \([l,r + 1]\),答案会增加 \(f(r + 1,[l,r]) = f(r + 1,[1,r]) - f(r + 1,[1,l - 1])\)。
所以对于一个区间的转移,我们可以分成两类:
-
一个前缀和一个其后面一个数产生的贡献,即为 \(f(i + 1,[1,i])\),这个东西可以使用前缀和记录。
-
\(r + 1\) 对于区间 \([1,l - 1]\) 的贡献,这个部分无法预处理,所以直接再次离线即可。
区域的区间变化方式,道理是相同的。
接下来处理第二次离线的方式。
我们使用扫描线来解决。对于所有未处理的询问,我们直接对于每个 \([1,i] \in [1,n]\),暴力求出每个区间需要的询问。
这样题目就被解决了!
我在代码中的第一种贡献并没有使用前缀和去记录,而是一个一个加的。由于指针移动的复杂度为 \(O(\sqrt n)\),所以这个并不会影响到代码的复杂度。
3.再来一道例题
有一道类似的例题也贴一下:博丽灵梦,这题需要使用二维分块+只减不增的回滚莫队,有兴趣的同学可以去做一下。
Part INF 一些例题
1.一个简单的询问
首先我们知道 \(\text{get}(l,r,x) = \text{get}(1,r,x) - \text{get}(1,l - 1,x)\)。
然后我们令 \(\text{g}(r,x) = \text{get}(1,r,x)\),所以答案就是
所以把每一个问题拆成 \(4\) 个子问题去求解即可。
但是这题的统计答案和以往有些许差别,所以给个代码:

2.这是我自己的发明
和上一题差不多,只是多了一个换根操作。
我们分成三种情况来讨论。
- 1.这个点就是根节点
区间就是从 1 到 \(n\)。
- 2.根节点被这个点包住
画个图观察一下就知道是这个点的子树为把原来根节点的子树挖掉。
- 3.这个点被根节点包住
这个是不变的。
所以最后要搜哪些区间我们就知道啦!代码如下:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号