连续段 dp - 状态转移时依赖相邻元素的序列计数问题

引入

在一类序列计数问题中，状态转移的过程可能与相邻的已插入元素的具体信息相关。

这类问题通常的特点是，如果只考虑在序列的一侧插入，问题将容易解决。

枚举插入顺序的复杂度通常难以接受，转移时枚举插入位置又难以记录已插入元素的信息。

所以我们就要用连续段 dp。

dp 模型

连续段 dp 的好处在于，他的元素插入只会在连续段的两端进行。

所以他只会通过 建立新段，插入至已有连续段的两端，合并两段 来进行转移。

通常地，我们会按某种特定的顺序插入所有元素。

每次插入元素时，对三类转移方式进行分类讨论：

1. 将插入的元素作为一个新连续段插入
2. 将元素插入至一个已有连续段的两端
3. 将元素用于合并两个连续段

分别会导致什么状态变化。

我们先从最基础的 dp 模型说起。

求满足某些限制的 $n$ 个元素的排列数量

我们一般会定义 $d{p}_{i,j}$ 为前 $i$，形成了 $j$ 个联通段的个数。

所以我们考虑三种情况。

1. 建立新的连续段：$d{p}_{i,j}\times (j+1)\to d{p}_{i+1,j+1}$
2. 合并两个连续段：$d{p}_{i,j}\times (j-1)\to d{p}_{i+1,j-1}$
3. 插入至已有连续段的两端：$d{p}_{i,j}\times 2\times j\to d{p}_{i+1,j}$（注意此时有可能左右不同，所以要分讨）

可能有人会对转移方程有问题。我下面用一张直观一点的图做一个解释。

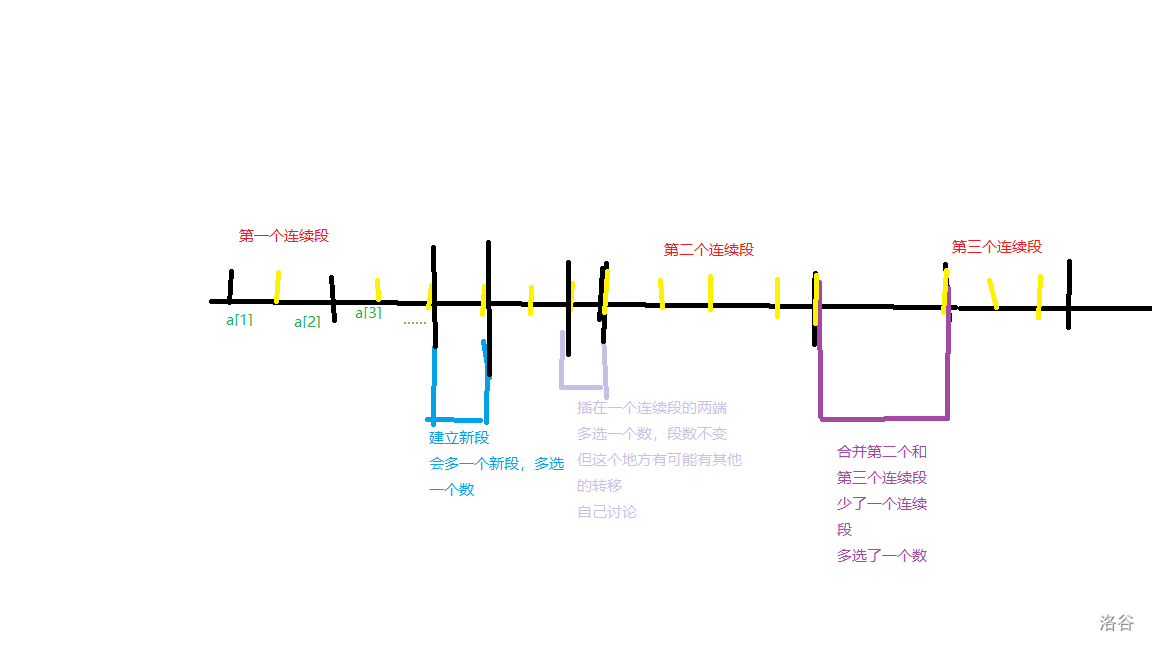
例题：

[COCI2021-2022#2] Magneti

考虑 DP。

令 $g_k$ 为放完所有小球后还剩下 $k$ 个空为的情况数。

所以容易推出 $\sum _{k=0}^{m-n}{g}_k\times {(}_k^{n+m-k})$ 就是答案。

现在问题转化成了怎么求 $g_k$。

考虑 DP。

$d{p}_{i,j,k}$ 表示放完前 $i$ 个小球，有 $j$ 个连续段，不能放球的位置有 $k$ 个。

然后在上面的式子改一改即可。

1. $(j+1)\times d{p}_{i,j,k}\to d{p}_{i+1,j+1,k+1}$

2. $(j-1)\times d{p}_{i,j,k}\to d{p}_{i+1,j-1,k+2\times r_{i+1}-1}$

3. $d{p}_{i,j,k}\times 2\times j\to d{p}_{i+1,j,k+r_{i+1}}$

所以就有代码啦！

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod = 1e9 + 7;
const int maxn = 55;
const int maxl = 10000 + 100;
int n,l;
int r[maxn],g[maxl];
int dp[maxn][maxn][maxl];
int fac[maxl],inv[maxl];
int qpow(int a,int b)
{
    int res = 1;
    while(b)
    {
        if(b & 1)
        {
            res = res * a % mod;
        }
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}
int C(int a,int b)
{
    return fac[a] * inv[b] % mod * inv[a - b] % mod;
}
signed main()
{
    fac[0] = inv[0] = 1;
    for(int i = 1;i < maxl;i++)
    {
        fac[i] = fac[i - 1] * i % mod;
        inv[i] = qpow(fac[i],mod - 2);
    }
    cin >> n >> l;
    for(int i = 1;i <= n;i++)
    {
        cin >> r[i];
    }
    sort(r + 1,r + n + 1);
    dp[0][0][0] = 1;
    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j <= i;j++)
        {
            for(int k = 0;k < l;k++)
            {
                if(k + r[i + 1] <= l)//插入在一个连续段的两端
                {
                    dp[i + 1][j][k + r[i + 1]] = (dp[i + 1][j][k + r[i + 1]] + dp[i][j][k] * j * 2 % mod) % mod;
                }
                if(k + 2 * r[i + 1] - 1 <= l && j >= 2)//合并两个新段
                {
                    dp[i + 1][j - 1][k + 2 * r[i + 1] - 1] = (dp[i + 1][j - 1][k + 2 * r[i + 1] - 1] + dp[i][j][k] * (j - 1) % mod) % mod;
                }
                if(k + 1 <= l)
                {
                    dp[i + 1][j + 1][k + 1] = (dp[i + 1][j + 1][k + 1] + dp[i][j][k] * (j + 1) % mod) % mod;//增加一个段
                }
            }
        }
    }
    for(int i = 0;i <= l;i++)
    {
        g[i] = dp[n][1][i];
    }
    int ans = 0;
    for(int i = 0;i <= l;i++)
    {
        ans = (ans + C(l - i + n,n) * g[i] % mod) % mod;
    }
    cout << ans;
    return 0;
}