C#实现二叉查找树

简介

    树是一种非线性结构。树的本质是将一些节点由边连接起来，形成层级的结构。而二叉树是一种特殊的树，使得树每个子节点必须小于等于2.而二叉查找树又是一类特殊的二叉树。使得每一个节点的左节点或左子树的所有节点必须小于这个节点，右节点必须大于这个节点。从而方便高效搜索。

    下面来看如何使用C#实现二叉查找树。

 

实现节点

    二叉查找树是节点的集合。因此首先要构建节点，如代码1所示。

    //二叉查找树的节点定义
    public class Node
    {
        //节点本身的数据
        public int data;
        //左孩子
        public Node left;
        //右孩子
        public Node right;
        public void DisplayData()
        {
            Console.Write(data+" ");
        }
    }

    代码1.节点的定义

 

构建二叉树

    构建二叉树是通过向二叉树插入元素得以实现的，所有小于根节点的节点插入根节点的左子树，大于根节点的，插入右子树。依此类推进行递归。直到找到位置进行插入。二叉查找树的构建过程其实就是节点的插入过程。C#实现代码如代码2所示。

        public void Insert(int data)
        {
            Node Parent;
            //将所需插入的数据包装进节点
            Node newNode=new Node();
            newNode.data=data;

            //如果为空树，则插入根节点
            if(rootNode==null)
            {
                rootNode=newNode;
            }
            //否则找到合适叶子节点位置插入
            else
            {
                Node Current = rootNode;
                while(true)
                {
                    Parent=Current;
                    if(newNode.data<Current.data)
                    {
                        Current=Current.left;
                        if(Current==null)
                        {
                            Parent.left=newNode;
                            //插入叶子后跳出循环
                            break;
                        }
                    }
                    else
                    {
                        Current = Current.right;
                        if (Current == null)
                        {
                            Parent.right = newNode;
                            //插入叶子后跳出循环
                            break;
                        }
                    }
                }
            }
        }

   代码2.实现二叉树的插入

 

二叉树的遍历

    二叉树的遍历分为先序(PreOrder)，中序(InOrder)和后序(PostOrder)。先序首先遍历根节点，然后是左子树，然后是右子树。中序首先遍历左子树，然后是根节点，最后是右子树。而后续首先遍历左子树，然后是右子树，最后是根节点。因此，我们可以通过C#递归来实现这三种遍历，如代码3所示。

        //中序
        public void InOrder(Node theRoot)
        {
            if (theRoot != null)
            {
                InOrder(theRoot.left);
                theRoot.DisplayData();
                InOrder(theRoot.right);
            }
        }
        //先序
        public void PreOrder(Node theRoot)
        {
            if (theRoot != null)
            {
                theRoot.DisplayData();
                PreOrder(theRoot.left);
                PreOrder(theRoot.right);
            }
        }
        //后序
        public void PostOrder(Node theRoot)
        {
            if (theRoot != null)
            {
                PostOrder(theRoot.left);
                PostOrder(theRoot.right);
                theRoot.DisplayData();
            }
        }

   代码3.实现二叉排序树的先序，中序和后续遍历

 

找到二叉查找树中的最大值和最小值

    二叉查找树因为已经有序，所以查找最大值和最小值非常简单，找最小值只需要找最左边的叶子节点即可。而找最大值也仅需要找最右边的叶子节点，如代码4所示。

 //找到最大节点
        public void FindMax()
        {
            Node current = rootNode;
            //找到最右边的节点即可
            while (current.right != null)
            {
                current = current.right;
            }
            Console.WriteLine("\n最大节点为:" + current.data);

        }
        //找到最小节点
        public void FindMin()
        {
            Node current = rootNode;
            //找到最左边的节点即可
            while (current.left != null)
            {
                current = current.left;
            }
            Console.WriteLine("\n最小节点为:" + current.data);
        }

   代码4.二叉查找树找最小和最大节点

 

二叉查找树的查找

    因为二叉查找树已经有序，所以查找时只需要从根节点开始比较，如果小于根节点，则查左子树，如果大于根节点，则查右子树。如此递归，如代码5所示。

//查找
        public Node Search(int i)
        {
            Node current = rootNode;
            while (true)
            {
                if (i < current.data)
                {
                    if (current.left == null)
                        break;
                    current = current.left;
                }
                else if (i > current.data)
                {
                    if (current == null)
                        break;
                    current = current.right;
                }
                else
                {
                    return current;
                }
            }
            if (current.data != i)
            {
                return null;
            }

            return current;
        }

    代码5.二叉查找树的查找

 

二叉树的删除

    二叉树的删除是最麻烦的，需要考虑四种情况：

•      被删节点是叶子节点
•      被删节点有左孩子没右孩子
•      被删节点有右孩子没左孩子
•      被删节点有两个孩子

 

    我们首先需要找到被删除的节点和其父节点，然后根据上述四种情况分别处理。如果遇到被删除元素是根节点时，还需要特殊处理。如代码6所示。

//删除二叉查找树中的节点，最麻烦的操作
        public Node Delete(int key)
        {
            Node parent = rootNode;
            Node current = rootNode;
            //首先找到需要被删除的节点&其父节点
            while (true)
            {
                if (key < current.data)
                {
                    if (current.left == null)
                        break;
                    parent = current;
                    current = current.left;
                }
                else if (key > current.data)
                {
                    if (current == null)
                        break;
                    parent = current;
                    current = current.right;
                }
                //找到被删除节点，跳出循环
                else
                {
                    break;
                }
            }
            //找到被删除节点后，分四种情况进行处理
            //情况一，所删节点是叶子节点时，直接删除即可
            if (current.left == null && current.right == null)
            {
                //如果被删节点是根节点，且没有左右孩子
                if (current == rootNode&&rootNode.left==null&&rootNode.right==null)
                {
                    rootNode = null;
                }
                else if (current.data < parent.data)
                    parent.left = null;
                else
                    parent.right = null;
            }
            //情况二，所删节点只有左孩子节点时
            else if(current.left!=null&&current.right==null)
            {
                if (current.data < parent.data)
                    parent.left = current.left;
                else
                    parent.right = current.left;
                
                
            }
            //情况三，所删节点只有右孩子节点时
            else if (current.left == null && current.right != null)
            {
                if (current.data < parent.data)
                    parent.left = current.right;
                else
                    parent.right = current.right;

                
            }
            //情况四，所删节点有左右两个孩子
            else
            {
                //current是被删的节点，temp是被删左子树最右边的节点
                Node temp;
                //先判断是父节点的左孩子还是右孩子
                if (current.data < parent.data)
                {

                    parent.left = current.left;
                    temp = current.left;
                    //寻找被删除节点最深的右孩子
                    while (temp.right != null)
                    {
                        temp = temp.right;
                    }
                    temp.right = current.right;
                    
                    
                }
                //右孩子
                else if (current.data > parent.data)
                {
                    parent.right = current.left;
                    temp = current.left;
                    //寻找被删除节点最深的左孩子
                    while (temp.left != null)
                    {
                        temp = temp.left;
                    }
                    temp.right = current.right;
                }
                //当被删节点是根节点，并且有两个孩子时
                else
                {
                    temp = current.left;
                    while (temp.right != null)
                    {
                        temp = temp.right;
                    }
                    temp.right = rootNode.right;
                    rootNode = current.left;
                }
                    
            }
            return current;

        }

   代码6.二叉查找树的删除

 

测试二叉查找树  

    现在我们已经完成了二叉查找树所需的各个功能，下面我们来对代码进行测试:

BinarySearchTree b = new BinarySearchTree();
            /*插入节点*/
            b.Insert(5);
            b.Insert(7);
            b.Insert(1);
            b.Insert(12);
            b.Insert(32);
            b.Insert(15);
            b.Insert(22);
            b.Insert(2);
            b.Insert(6);
            b.Insert(24);
            b.Insert(17);
            b.Insert(14);
            /*插入结束 */
            
            /*对二叉查找树分别进行中序，先序，后序遍历*/
            Console.Write("\n中序遍历为:");
            b.InOrder(b.rootNode);
            Console.Write("\n先序遍历为:");
            b.PreOrder(b.rootNode);
            Console.Write("\n后序遍历为:");
            b.PostOrder(b.rootNode);
            Console.WriteLine(" ");
            /*遍历结束*/

            /*查最大值和最小值*/
            b.FindMax();
            b.FindMin();
            /*查找结束*/

            /*搜索节点*/
            Node x = b.Search(15);
            Console.WriteLine("\n所查找的节点为" + x.data);
            /*搜索结束*/

            /*测试删除*/
            b.Delete(24);
            Console.Write("\n删除节点后先序遍历的结果是:");
            b.InOrder(b.rootNode);
            b.Delete(5);
            Console.Write("\n删除根节点后先序遍历的结果是:");
            b.InOrder(b.rootNode);
            Console.ReadKey();
            /*删除结束*/

   代码7.测试二叉查找树

 

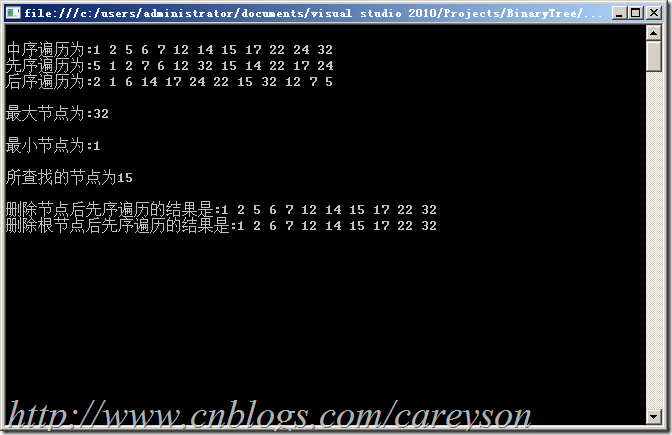
   运行结果如图1所示：

   

    图1.测试运行结果

 

总结

    树是节点的层级集合，而二叉树又是将每个节点的孩子限制为小于等于2的特殊树，二叉查找树又是一种特殊的二叉树。二叉树对于查找来说是非常高效，尤其是查找最大值和最小值。