NC51267 Knights of the Round Table
题目链接
https://ac.nowcoder.com/acm/problem/51267
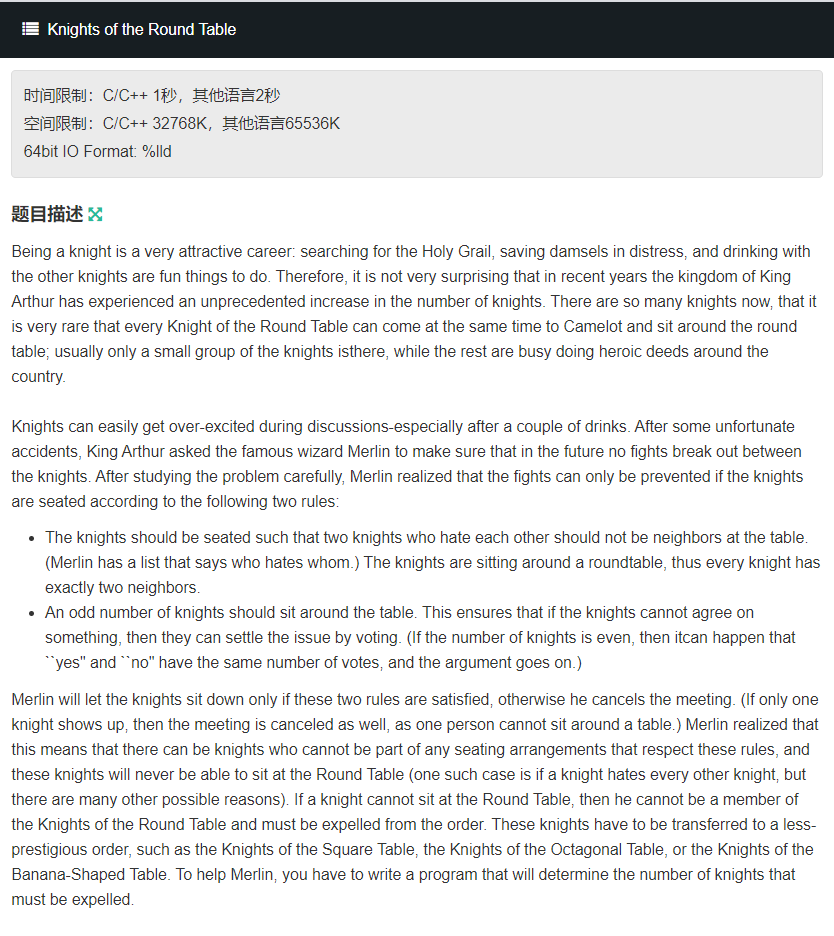
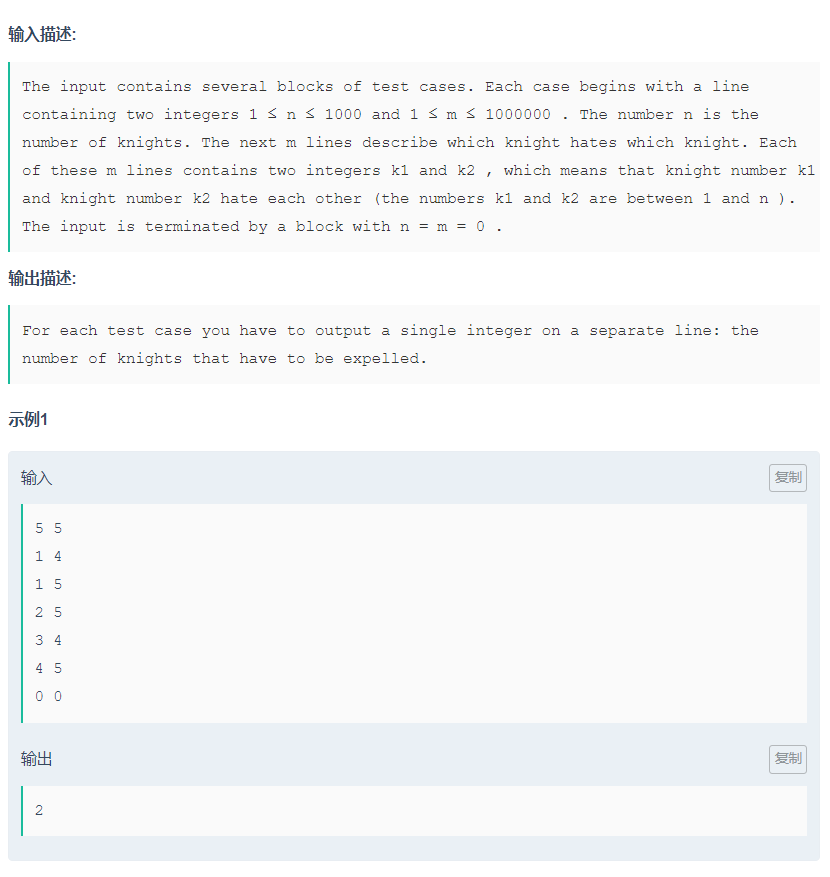
题意
求无向图中不在奇圈上的点。
思路
1.如果一个双连通分量内的某些顶点在一个奇圈中(即双连通分量含有奇圈),那么这个双连通分量的其他顶点也在某个奇圈中;
2.如果一个双连通分量含有奇圈,则他必定不是一个二分图。反过来也成立,这是一个充要条件。
基于以上俩点, Tarjan求出每个点双连通图分量后,用交叉染色法判断是否存在奇圈!
AC代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e6 + 50;
const int N = 1050;
struct node{
int to, next;
} edge[maxn];
int top, stack1[maxn];
int tot, cnt, dccn;
int dfn[N], low[N];
int head[N];
vector<int> dcc[N];
void add(int from, int to){
edge[++cnt].to = to;edge[cnt].next = head[from];head[from] = cnt;
}
void ins(int u, int v){add(u, v); add(v, u);}
void Tarjan(int u, int rt){
dfn[u] = low[u] = ++tot;
if(rt == u && head[u] == -1){
dccn++;
dcc[dccn].clear();
dcc[dccn].push_back(u);
return;
}
stack1[++top] = u;
for(int i = head[u];i != -1;i = edge[i].next){
int v = edge[i].to;
if(!dfn[v]){
Tarjan(v, rt);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]){
dccn++;
dcc[dccn].clear();
dcc[dccn].push_back(u);
while (1){
int w = stack1[top];
dcc[dccn].push_back(w);
top--;
if (w == v){ // 做到子树全部弹出为止,不是u,不然v的兄弟也会被弹出
break;
}
}
}
}
else low[u] = min(low[u], dfn[v]);
}
}
int now[N], col[N], vis[N];
bool dfs(int u, int c){
col[u] = c;
for(int i = head[u];i != -1;i = edge[i].next){
int v = edge[i].to;
if(!now[v]) continue;
if(col[v] == c) return false;
if(col[v] == 0 && !dfs(v, 3 - c)) return false;
}
return true;
}
int mp[N][N];
void init(){
cnt = 0; tot = 0, dccn = 0, top = 0;
memset(head, -1, sizeof(head));
memset(mp, 0, sizeof(mp));
memset(low, 0, sizeof(low));
memset(dfn, 0, sizeof(dfn));
memset(vis, 0, sizeof(vis));
}
int main()
{
std::ios::sync_with_stdio(false);
int n, m;
while(cin >> n >> m){
if(n == 0 && m == 0) break;
init();
for(int i = 0;i < m;i++){
int u, v;
cin >> u >> v;
mp[u][v] = mp[v][u] = 1;
}
for(int i = 1;i <= n;i++){
for(int j = i + 1;j <= n;j++){
if(mp[i][j] == 0){
ins(i, j);
}
}
}
for(int i = 1;i <= n;i++) if(!dfn[i]) Tarjan(i, i);
for(int i = 1;i <= dccn;i++){
memset(now, 0, sizeof(now));
memset(col, 0, sizeof(col));
for(int j = 0;j < dcc[i].size();j++){
now[dcc[i][j]] = 1;
}
if(!dfs(dcc[i][0], 1)){
for(int j = 0;j < dcc[i].size();j++){
vis[dcc[i][j]] = 1;
}
}
}
int ans = 0;
for(int i = 1;i <= n;i++) if(!vis[i]) ans++;
cout << ans << endl;
}
return 0;
}


