CodeForce 387D. George and Interesting Graph

题目链接

https://codeforces.com/problemset/problem/387/D

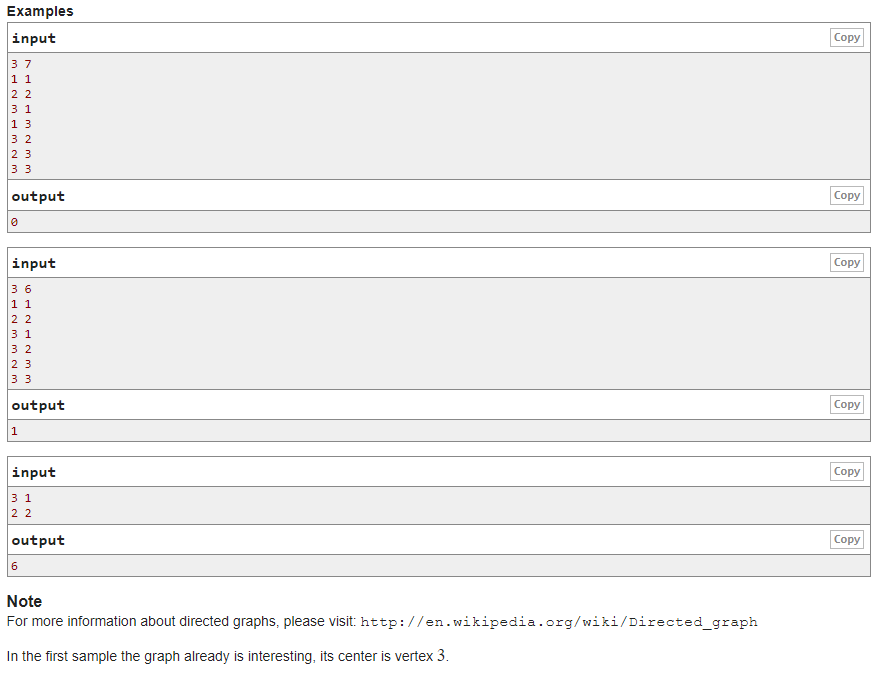
题意

思路

\(N\)不大，考虑枚举中心点\(u\)， 首先和\(u\)相连的边加上自环共有\(2 * n - 1\)条， 那么将不够的边补上。
每个边都和\(u\)有双向边之后， 入度和出度还剩1.
将剩下\(n - 1\) 个点拆成入度点和出度点， 那么每个点的入度和出度必须有连边， 那么将原图建成二分图跑最大匹配后将多余边删去，不足的补上即可。

AC代码

#include<iostream>
#include<cstdio>
#include<vector>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<map>
using namespace std;
typedef long long ll;
const int maxn = 2000 + 50;
vector<int> G[maxn];
int match[maxn], used[maxn];
int tot;
void add(int u, int v){
    G[u].push_back(v);
    G[v].push_back(u);
}
bool dfs(int v){
    used[v] = 1;
    for(int i = 0;i < G[v].size();i++){
        int u = G[v][i];
        int w = match[u];
        if(w < 0 || !used[w] && dfs(w)){
            match[v] = u;
            match[u] = v;
            return true;
        }
    }
    return false;
}
int max_matching(){
    int ans = 0;
    memset(match, -1, sizeof(match));
    for(int i = 1;i <= tot;i++){
        if(match[i] < 0){
            memset(used, 0, sizeof(used));
            if(dfs(i)) ans++;
        }
    }
    return ans;
}
int n, m;
int mp[maxn][maxn];
int u[maxn], v[maxn];
int main()
{
    std::ios::sync_with_stdio(false);
    cin >> n >> m;
    for(int i = 1;i <= m;i++){
        cin >> u[i] >> v[i];
        mp[u[i]][v[i]] = 1;
    }
    int ans = 0x3f3f3f3f;
    tot = 2 * n;
    for(int i = 1;i <= n;i++){
        int sum = 0;
        for(int j = 1;j <= n;j++){
            if(!mp[i][j]) sum++;
            if(i != j && !mp[j][i]) sum++;
        }
        int cnt = m - (2 * n - 1 - sum);
        for(int i = 0;i <= tot;i++) G[i].clear();
        for(int j = 1;j <= m;j++){
            int a = u[j], b = v[j];
            if(a != i && b != i){
                add(a, b + n);
            }
        }
        int c = max_matching();
        sum += cnt - c;
        cnt = 0;
        for(int j = 1;j <= 2 * n;j++){
            if(match[j] == -1 && j != i && j != i + n){
                cnt++;
            }
        }
        ans = min(ans, sum + cnt / 2);
    }
    cout << ans << endl;

    return 0;
}