条形码问题

前言

这题是前天，对，没错前天的模拟赛做到的。然而我今天才订正完。

题面

条形码是一种由亮条(Light Bar)和暗条(Dark Bar)交替出现且以暗条为起头的符号，每条都占有若干个单位宽。图33-1给出了一个含有4个条的条形码它延续了1+2+3+1=7单位的宽 。

 

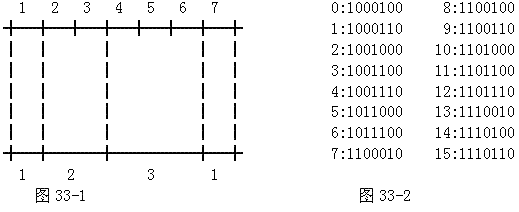
一般情况下BC(N,K,M)是一个包含所有由K个条总宽度正好为N个单位，每个条的宽度至多为M个单位性质的条形码组成的集合。

例如：图33-1的条形码属于BC(7,4,3)而不属于BC(7,4,2)。

图33-2显示了集合BC(7,4,3)中的所有16个符号，其中1表示暗，0表示亮。

图中所示条形码已按字典顺序排列冒号左边数字为条形码码的编号，图33-1的条形码在BC(7,4,3)书的编为4。

 输入

输入的第一行为Ｎ、Ｋ、Ｍ的值（1≤N,K,M≤33）。

第二行为数字S(0≤S≤100)，而后的S行中，每行为一个图33-2那样描述的集合BC(N,K,M)中的一个条形码。

输出

你的程序应完成任务 

1. 第一行是BC(N,K,M)中条形码的个数 
2. 第二行起的S行中，每一行是输入文件对应条形码的编号；输入与输出数据中同一行相邻两个数之间用空格区分。

分析

§ 1 枚举？

理论上可行，但因为有每条宽上线M的限制，因此枚举时并不只是像生成全排列那样简单，需要注意的细节很多。

§ 2 换个思路

我们考虑一下类似于Canter Expansion的思路，就是说把当前要求的条形码序列分解，然后求之前总的条形码个数，也就是当前的编号。（如何详细描述呢？我也不是很好表达，不明白的同学可以去看一下关于Canter Expansion的文章）

§ 3 动态规划

没错，我们用DP来求那个“之前总的条形码个数”。

设DP[i][j][k][x]表示由j个条总宽度正好为i个单位，首条的颜色为x，宽度为k个单位的条形码的编号。

则有DP[i][j][k][x] = ∑DP[i - 1][j][k - 1][x] + ∑DP[i - 1][j - 1][l][!x]

其中1 ≤ l ≤ M, !x表示与x相反的颜色。

参考代码

要点均注在注释中

#include <cstdio>
const int MAXN = 35;

int N, K, M, S, DP[MAXN][MAXN][MAXN][2];
char str[MAXN];

void init();

int main() {
    scanf("%d%d%d%d", &N, &K, &M, &S);
    init();
    int i, ans = 0, cnt, len, j, k, tmp1, tmp2;
    for (i = 1; i <= M; i++) ans += DP[N][K][i][1];　　// 总的条形码个数
    printf("%d\n", ans);
    for (i = 0; i < S; i++) {
        scanf("%s", str);
        cnt = len = 1; ans = 0;　　// cnt记录当前统计到的条码数，len记录当前条宽度
        for (j = 1; j < N; j++) {
            if (str[j] == '1') {
                if (str[j - 1] == '1')
                    for (k = 1, tmp1 = N - j, tmp2 = K - cnt; k <= M; k++) ans += DP[tmp1][tmp2][k][0];　　// 如果是暗条，那么累加1~M长度的亮条
                else for (k = M - len, tmp1 = N - j, tmp2 = K - cnt + 1; k > 0; k--) ans += DP[tmp1][tmp2][k][0];　　// 如果是亮条，那么要减去这条亮条长度
            }
            if (str[j] == str[j - 1]) len++;
            else cnt++, len = 1;
        }
        printf("%d\n", ans);
    }
    return 0;
}

void init() {　　// DP数组初始化，由前推后，这样实现比较简单
    DP[1][1][1][1] = DP[1][1][1][0] = 1;
    int i, j, k;
    for (i = 1; i < N; i++) 
        for (j = 1; j <= K; j++)
            for (k = 1; k <= M; k++) {
                if (k < M) DP[i + 1][j][k + 1][0] += DP[i][j][k][0];
                DP[i + 1][j + 1][1][1] += DP[i][j][k][0];
                if (k < M) DP[i + 1][j][k + 1][1] += DP[i][j][k][1];
                DP[i + 1][j + 1][1][0] += DP[i][j][k][1];
            }
}

总结

这题的满分思路比较难考虑到，说实话暴力都很难写，我也是看了dalao的AC代码才明白的。

重点呢在于你把编号转换成方案数，再导出这个转移方程的过程。

当然这篇博客不得不说我写得有些含糊，当然我自己明白，可是我是真的表达不出来。