Python-PuLP库学习

PuLP 解线性规划问题

线性规划问题概述

一般线性规划问可以表述为

其中a、b、c均是已知的参数

满足所有约束条件的解，称为线性规划问题的可行解；

所有可行解构成的集合，称为可行域。

使目标函数达到最小值的解，称为最优解。

线性规划问题的解决通常为以下过程：

1. 确定变量、约束条件
2. 构造目标函数、建立数学方程、确定参数
3. 解出可行域和最优解

用PuLP库解线性规划模型

例题1 ：

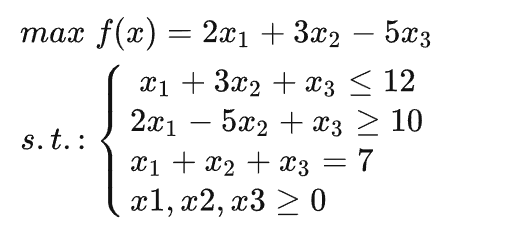
导入PuLP库

import pulp

问题初始化

LPprob = pulp.LpProblem("Lpproblem",sense = pulp.LpMaximize)
#代码中的LpProblem方法是定义问题的构造函数
#“Lpproblem”是定义的问题名称，用于输出信息
#参数 sense是用来指定优化方向（是求最大还是最小）
#最大值用参数 pulp.LpMaximize
#最小值用参数 pulp.LpMinimize

定义变量

基本方法

x1 = pulp.LpVariable('x1',lowBound = 0 , upBound = 7, cat = 'Continuous')
x2 = pulp.LpVariable('x2',lowBound = 0 , upBound = 7, cat = 'Continuous')
x3 = pulp.LpVariable('x3',lowBound = 0 , upBound = 7, cat = 'Continuous')
#‘x1’是定义的变量名
#lowBound和upBound 是定义变量取值的上下界 ， 可以不加定义，默认为负无穷大到正无穷大
#cat 定义变量类型 
##‘Continuous’是连续型变量（默认）
##‘Integer’ 表示离散变量（用于整数规划问题）
##‘Binary’表示0/1变量（用于0-1规划问题）

 

定义目标函数

LPprob += 2*x1 + 3*x2 - 5*x3
#在问题初始化中定义的问题变量名称 += 目标函数式

添加约束条件

LPprob += (2*x1 - 5*x2 + x3 >= 10)  # 不等式约束
LPprob += (x1 + 3*x2 + x3 <= 12)  # 不等式约束
LPprob += (x1 + x2 + x3 == 7)  # 等式约束
#问题变量名 +=(约束条件表达式)
#特别注意等于是两个等号！

 输出求解结果

LPprob.solve() #
print('Status:',pulp.LpStatus[LPprob.status])#输出求解状态 有可能是无解
for i in LPprob.variables():
    print(i.name,"=" , i.varValue) #输出每个变量的最优解
print（"F(x) = " , pulp.value(LPprob.objective)) #输出最优解所对应的目标函数值