#luogu整理 P1244 青蛙过河

luogu P1244 青蛙过河

这个题太骚了。。。。

题目描述

有一条河，左边一个石墩（\(A\) 区）上有编号为 \(1,2,\ldots ,n\) 的 \(n\) 只青蛙，河中有 \(k\) 个荷叶（C 区），还有 \(h\) 个石墩（D 区），右边有一个石墩（B 区），如下图所示。\(n\) 只青蛙要过河（从左岸石墩 A 到右岸石墩 B），规则为：

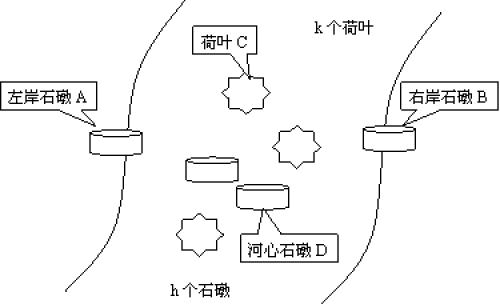
• 石墩上可以承受任意多只青蛙，荷叶只能承受一只青蛙（不论大小）；

• 青蛙可以：\(A→B（表示可以从 A 跳到 B，下同），A \to C，A \to D，C \to B，D \to B，D \to C，C \to D\)。

• 当一个石墩上有多只青蛙时，则上面的青蛙只能跳到比它大一号的青蛙上面。

你的任务是对于给出的 \(h,k\)，计算并输出最多能有多少只青蛙可以根据以上规则顺利过河。

输入格式

输入两个整数 \(h,k\)。

输出格式

一个整数，表示最多能有多少只青蛙可以根据以上规则顺利过河。

输入样例

2 3

输出样例

16

数据范围

\(h≤20，k \leq 10^3\)

思路

先理解一下题意：青蛙一开始都在左边岸上，且先跳出的青蛙体型比后跳出的青蛙体型小（也就是先跳出的青蛙能坐在后跳出的青蛙上），青蛙可以选择直接向河对岸跳，也可以从荷叶区、河墩区中转一下到对岸。需要注意的是：一片河墩上面的第一个青蛙，决定了这个河墩上青蛙的最大体型。（有点类似汉诺塔）

动态规划，设\(f[h][k]\)表示用了h个河墩，k个荷叶最多的过河数量，那么我们可以知道\(f[0][k] = k+1\)（前k个先到荷叶上，最后一个直接到河对岸，前k个再到对岸）。

如果多用一个河墩，我们就有：\(f[1][k] = f[0][k] + f[0][k] = 2f[0][k]\)含义：先让第一队青蛙用这k个荷叶中转到河墩区河墩上（也就是\(f[0][k]\)只），再用让第二队青蛙通过荷叶直接到对岸（\(f[0][k]\)只）。最后让第一队的青蛙继续利用荷叶中转到对岸。整个过程符合题目要求。

两个河墩，我们就可以让第一队青蛙利用k个荷叶和一号河墩中转（\(f[1][k]\)只），到河墩区的二号河墩上，再让二队青蛙利用k个荷叶中转到一号河墩上（\(f[0][k]\)只），再让第三队的青蛙直接利用荷叶中转到对岸（\(f[0][k]\)只），最后二队青蛙过岸、一队青蛙过岸，就算是完成了，总数是\(f[2][k] = f[0][k]+f[0][k]+f[1][k] = 4f[0][k]\)只。

最终通过整理，我们发现：\(f[h][k] = f[0][k] \times 2^h = (k+1) \times 2^h\)。

代码

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

int main(){
    int h,k;
    cin >> h >> k;
    cout << (k+1)*(1 << h) << endl;
    return 0;
}