BZOJ 4927 第一题

题目链接

https://www.lydsy.com/JudgeOnline/problem.php?id=4927

题解

6个木棍拼成一个正方形，只有下面两种情况：

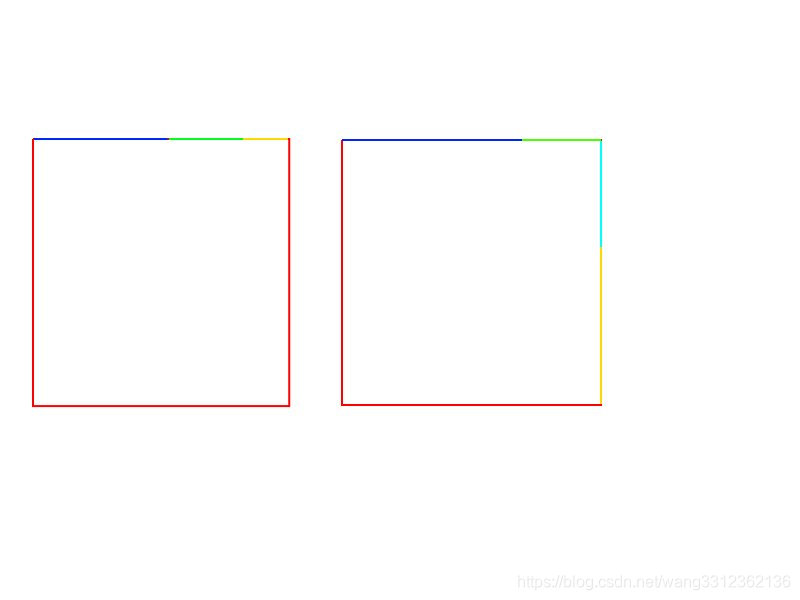
第一种情况

排序，先枚举蓝色边，再枚举红色边，那么绿色边+黄色边的值已经确定了，记$sum[i]$表示两条边之和为$i$的方案数，对于每个枚举到的蓝色边和红色边，加入答案即可。$sum$可以由蓝色边更新。

第二种情况

排序去重，先枚举红色边，再枚举蓝色边，记黄色边的长度大于蓝色边长度时，黄色边和天蓝色边的构成方案数为$past$，已知蓝色边，为了不重复枚举，要么由一条长度为蓝色和一条$past$中统计过的边构成，要么由两条长度为蓝色的边构成。

细节比较麻烦，需要想清楚。

代码

#include <cstdio>
#include <algorithm>
 
int read()
{
  int x=0,f=1;
  char ch=getchar();
  while((ch<'0')||(ch>'9'))
    {
      if(ch=='-')
        {
          f=-f;
        }
      ch=getchar();
    }
  while((ch>='0')&&(ch<='9'))
    {
      x=x*10+ch-'0';
      ch=getchar();
    }
  return x*f;
}
 
const int maxn=5000;
const int maxv=10000000;
 
int n,v[maxn+10],f[maxn+10],cnt[maxn+10],tot,num[maxv+10],sum[maxv+10];
long long ans;
 
long long C(int x,int y)
{
  if(x<y)
    {
      return 0ll;
    }
  long long res=x;
  for(int i=2; i<=y; ++i)
    {
      res=res*(x-i+1)/i;
    }
  return res;
}
 
int main()
{
  n=read();
  for(int i=1; i<=n; ++i)
    {
      v[i]=read();
    }
  std::sort(v+1,v+n+1);
  for(int i=1; i<=n; ++i)
    {
      ++num[v[i]];
    }
  for(int i=3; i<n; ++i)
    {
      for(int j=1; j<i-1; ++j)
        {
          if(v[i-1]+v[j]<=maxv)
            {
              ++sum[v[i-1]+v[j]];
            }
        }
      int now=i+1;
      while(now<=n)
        {
          if(num[v[now]]>=3)
            {
              ans+=1ll*sum[v[now]-v[i]]*C(num[v[now]],3);
            }
          while(v[now+1]==v[now])
            {
              ++now;
            }
          ++now;
        }
    }
  tot=std::unique(v+1,v+n+1)-v-1;
  for(int i=2; i<=tot; ++i)
    {
      long long past=0;
      int fuckpps=num[v[i]]*(num[v[i]]-1)/2;
      for(int j=i-1; (j>0)&&(v[j]*2>=v[i]); --j)
        {
          ans+=1ll*past*((v[j]*2!=v[i])?(1ll*num[v[j]]*num[v[i]-v[j]]):(1ll*num[v[j]]*(num[v[j]]-1)/2))*fuckpps;
          if(v[j]*2!=v[i])
            {
              ans+=1ll*num[v[j]]*num[v[i]-v[j]]*(num[v[j]]-1)*(num[v[i]-v[j]]-1)/4*fuckpps;
            }
          else
            {
              ans+=1ll*C(num[v[j]],4)*fuckpps;
            }
          past+=1ll*num[v[j]]*num[v[i]-v[j]];
        }
    }
  printf("%lld\n",ans);
  return 0;
}