斯特林数相关

斯特林数 往往用于普通幂与下降幂的互相转换，也可以用来做一些计数问题。

有 第一类斯特林数 和 第二类斯特林数。我们用 \({n\brace m}\) 表示 第二类斯特林数，用 \({n\brack m}\) 表示 第一类斯特林数。

本文尽量采用比较“组合”的证明方式。当然，其中大部分式子都可以用数学归纳法证明。

第二类斯特林数

第二类斯特林数 \({n\brace m}\) 表示把 \(n\) 个不同小球放入 \(m\) 个相同盒子，盒子不能空的方案数。

例如把 \(4\) 个不同小球 \(\{1,2,3,4\}\) 放入 \(2\) 个相同盒子有 \(7\) 种方案，为：

\(\{1\}\{2,3,4\},\{2\}\{1,3,4\},\{3\}\{1,2,4\},\{4\}\{1,2,3\},\)

\(\{1,2\}\{3,4\},\{1,3\}\{2,4\},\{1,4\}\{2,3\}\)

所以 \({4\brace 2}=7\)。

规定：\(0\le n<m\) 时，\({n\brace m}=0\)。

\({n\brace m}\) 如何计算呢？

一、递推

考察 \(n\) 号小球所在的盒子。

• 如果为 \(n\) 号小球单独开一个盒子，此时的方案数即为 \({n-1\brace m-1}\)。

• 如果把 \(n\) 号小球放入先前开的盒子里，你要从先前已经有的 \(m\) 个盒子里选出一个来放它，方案数为 \(m{n-1\brace m}\)。

于是得到：

\[{n\brace m}={n-1\brace m-1}+m{n-1\brace m} \]

二、容斥

众所周知，把 \(n\) 个不同小球放入 \(m\) 个不同盒子，盒子可以空的方案数为 \(m^n\)。

先考虑把 \(n\) 个不同小球放入 \(m\) 个不同盒子，盒子不能空的方案数。根据容斥原理，必然是 总方案数 减去 钦定一个盒子空了的方案数，加上 钦定两个盒子空了的方案数……等于 \(\sum_{i=0}^m (-1)^i\binom mi(m-i)^n\)。

相比第二类斯特林数，刚刚那个东西只是多了盒子的顺序，于是有 \(m!{n\brace m}=\sum_{i=0}^m (-1)^i\binom mi(m-i)^n\)，也就是

\[{n\brace m}=\frac 1{m!}\sum_{i=0}^m (-1)^i\binom mi(m-i)^n \]

，这就是通项公式了。

贝尔数 \(b_n\)表示把 \(n\) 个不同小球放入若干个相同盒子，盒子不能空的方案数。第二类斯特林数每行的和为贝尔数，即 \(b_n=\sum_{j=0}^n{n\brace j}\)。但这不是本文的重点。

第一类斯特林数

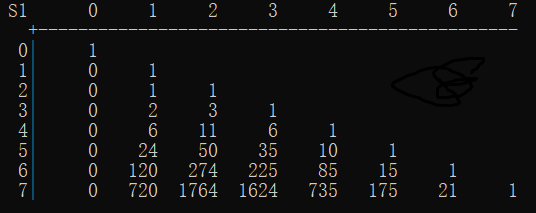
第一类斯特林数 \({n\brack m}\) 表示将 \(n\) 个不同元素划分为 \(m\) 个轮换的方案数。

例如把 \(4\) 个不同元素 \(\{1,2,3,4\}\) 划入 \(2\) 个轮换有 \(11\) 种方案，为：

\((1)(2,3,4),(1)(2,4,3),(2)(1,3,4),(2)(1,4,3),\)

\((3)(1,2,4),(3)(1,4,2),(4)(1,2,3),(4)(1,3,2),\)

\((1,2)(3,4),(1,3)(2,4),(1,4)(2,3)\)

所以 \({4\brack 2}=11\)。

规定：\(0\le n<m\) 时，\({n\brack m}=0\)。

\({n\brack m}\) 如何计算呢？

递推

考察 \(n\) 号元素所在的轮换。

• 如果为 \(n\) 号元素单独开一个轮换，此时的方案数即为 \({n-1\brack m-1}\)。

• 如果把 \(n\) 号元素放入先前的轮换里，那么你要从先前有的 \((n-1)\) 个间隙里选出一个来插入它，方案数为 \((n-1){n-1\brack m}\)。

于是得到：

\[{n\brack m}={n-1\brack m-1}+(n-1){n-1\brack m} \]

一些性质： \(\sum_{j=0}^n{n\brack j}=n!,{n\brack 1}=(n-1)!\)。

考虑大小为 \(n\) 的一个置换，必然可以分解为若干不相交轮换的复合。

例如置换\(\begin{pmatrix}1 & 2 & 3 & 4\\4 & 3 & 2 &1\\ \end{pmatrix}=(1\ 4)(2\ 3)\)。

则恰能分解为 \(m\) 个不相交轮换的 大小为 \(n\) 的置换 恰有 \({n\brack m}\) 个。

普通幂与下降幂的转换

下降幂：\(a^\underline b=\prod_{i=0}^{b-1}(a-i)\)，也即 \(A_a^b\)。

斯特林数可以用于普通幂与下降幂的互相转换。什么意思呢？

有如下式子：

\[x^n=\sum_{k=0}^n {n\brace k}x^\underline k\\x^\underline n=\sum_{k=0}^n (-1)^{n-k}{n\brack k}x^k \]

对于第一个式子，考虑用两种方法计算把 \(n\) 个不同小球放入 \(x\) 个不同盒子，盒子可以空的方案数：

• \(n\) 个球，每个球有 \(x\) 个盒子可以选，故为 \(x^n\)；
• 盒子不可以空的方案数为 \(x!{n\brace x}\) ；有球的盒子数为 \(k\) 时，方案数即 \(\binom xk k!{n\brace k}=x^{\underline k}{n\brace k}\)，故答案为 \(\sum_{k=0}^n {n\brace k}x^\underline k\\\)。

用两个式子算同一个东西，必然是相等的。

对于第二个式子，也能用类似的方法证明，可以自行思考。

借此，可以用第二类斯特林数加速求自然数 \(k\) 次幂和，如下：
\( S_m(n)=\sum_{i=0}^n i^m\\=\sum_{i=0}^n\sum_{j=0}^m{m\brace j}i^{\underline j}\\=\sum_{j=0}^m{m\brace j}\sum_{i=0}^ni^{\underline j}\\=\sum_{j=0}^m{m\brace j}j!\sum_{i=0}^n\binom ij\\=\sum_{j=0}^m{m\brace j}j!\binom{n+1}{j+1}\\=\sum_{j=0}^m{m\brace j}\frac 1{j+1}(n+1)^{\underline {j+1}} \)
其中 \(m\) 为正整数，\(n\) 为非负整数。

上升幂：\(a^\overline b=\prod_{i=0}^{b-1}(a+i)\)。

普通幂和上升幂也有类似的转换。

\[x^n=\sum_{k=0}^n {n\brace k}(-1)^{n-k}x^\overline k\\x^\overline n=\sum_{k=0}^n {n\brack k}x^k \]

斯特林反演

你发现式子 \(x^n=\sum_{k=0}^n {n\brace k}x^\underline k\) 的右边有个下降幂。

你闲得蛋疼想把下降幂转回普通幂。

你得到 \(x^n=\sum_{k=0}^n {n\brace k}x^\underline k\)

\(=\sum_{k=0}^n {n\brace k}\sum_{m=0}^k (-1)^{k-m}{k\brack m}x^m\)

\(=\sum_{m=0}^n\sum_{k=m}^n (-1)^{k-m}{n\brace k} {k\brack m}x^m\)

不论 \(x\) 取多少，左右两边都要相等。所以右边只有 \(x^n\) 的系数是 \(1\)，其它系数都是 \(0\)。

故 \(\sum_{k=m}^n (-1)^{k-m}{n\brace k} {k\brack m}=[m=n]\)

我们知道有一个二项式反演 \(f_n=\sum\limits_{j=0}^n(-1)^j{n\choose j}g_j\Leftrightarrow g_n=\sum\limits_{j=0}^n(-1)^j{n\choose j}f_j\)；

现在我们还有一个斯特林反演

\[f_n=\sum\limits_{j=0}^n(-1)^j{n\brace j}g_j\Leftrightarrow g_n=\sum\limits_{j=0}^n(-1)^j{n\brack j}f_j \]

这里只证从右推到左（从左推到右是类似的）。

\(f_n=\sum_{j=0}^n [j=n]f_j\)

\(=\sum_{j=0}^n\sum_{k=j}^n (-1)^{k-j}{n\brace k} {k\brack j}f_j\)

\(=\sum_{k=0}^n(-1)^k{n\brace k} \sum_{j=0}^k (-1)^{j}{k\brack j}f_j\)

\(=\sum_{k=0}^n(-1)^k{n\brace k} g_k\)

小练习

1.当 \(n\) 或 \(k\) 变成负整数的时候，怎样定义 \({n\brace k}\) 和 \(n\brack k\) 才能满足递推式？

2.讨论 \(\sum_{k=0}^n(-1)^k{n\brack k}\) 的值。

更快速的计算

以下不一定是最快的做法，但都只有一只 \(\log\)。

第二类斯特林数·行

由通项公式：\({n\brace m}=\frac 1{m!}\sum_{i=0}^m \binom mi(-1)^i(m-i)^n\)。

明显是一个卷积，于是做到 \(O(n\log n)\)。

第二类斯特林数·列

\({n\brace m}\) 是把 \(n\) 个不同小球放入 \(m\) 个相同盒子，盒子不能空的方案数。

设 \(G(x)\) 为非空集合的 \(\mathbf {EGF}\) ，\(F_m(x)\) 为第二类斯特林数第 \(m\) 列的的 \(\mathbf{EGF}\)，则有 \(F_m(x)=\frac 1{m!}G^m(x)\)。

就是一个多项式快速幂，\(O(n\log n)\)。

第一类斯特林数·行

\(x^\overline n=\sum_{k=0}^n {n\brack k}x^k\)，你发现这恰好就是第一类斯特林数第 \(n\) 行的 \(\mathbf {OGF}\)。

由 \(x^{\overline n}=\prod_{i=0}^{n-1}(x+i)\)，就可以分治做到 \(O(n\log^2n)\) 了。

但是可以更快。由上可得：

• \(x^\overline{n+1}=x^{\overline n}(x+n+1)\)

• \(x^\overline{2n}=x^{\overline n}(x+n)^{\overline n}\)

  \(=x^\overline n\sum_{k=0}^n {n\brack k}(x+n)^k\)

  \(=x^\overline n\sum_{k=0}^n {n\brack k}\sum_{j=0}^k{k\choose j} n^{k-j}x^j\)

  \(=x^\overline n\sum_{j=0}^nx^j\sum_{k=j}^n {n\brack k}{k\choose j} n^{k-j}\)
  可以看出一个卷积。

每次卷积是 \(O(n\log n)\) 的，长度每次翻倍，类似 多项式求逆的分析，可得总复杂度 \(O(n\log n)\)。

第一类斯特林数·列

注意，\(n\brack m\) 表示恰能分解为 \(m\) 个不相交轮换的 大小为 \(n\) 的置换的个数。

设 \(G(x)\) 为轮换的 \(\mathbf{EGF}\)，\(F_m(x)\) 为第一类斯特林数第 \(m\) 列的的 \(\mathbf{EGF}\)，则有 \(F_m(x)=\frac 1{m!}G^m(x)\)。

多项式快速幂，\(O(n\log n)\)。

例题

Cards（CF1278F，加强版：luogu P6031）

有 \(m\) 张牌，其中有一张是王牌。将这些牌均匀随机打乱 \(n\) 次，设有 \(x\) 次第一张为王牌，求 \(x^k\) 的期望值。

答案对 \(998244353\) 取模。

\(1\le k\le 5000\)，\(1\le n,m<998244353\)

加强版：\(1\le k\le 10^7\)，\(1\le n,m<998244353\)

方阵（2018 雅礼集训1-16）

给出一个 \(n\times m\) 的矩形，每个位置可以填上 \([1,c]\) 中的任意一个数，要求填好后 任意两行互不相同 且 任意两列互不相同，两行或两列相同 当且仅当 对应位置都相等，求方案数。

答案对 \(1004535809\) 取模。

\(1\le n,m\le 5000,1\le c<1004535809\)

更多题目

9019 10237 序列计数

FJOI2016 建筑师（加强版：CF960G）

CF932E Team Work

luogu P6620 组合数问题

luogu P4827 Crash 的文明世界

9019 10347 矩阵

BZOJ 4671 异或图

更更多题目

luogu P4091 求和

CF715E Complete the Permutations

CF961G Partitions

参考资料《具体数学》