从 简单容斥 到 min-max 容斥 与 二项式反演
证明基本都是自己瞎证的，如果证法比较丑请见谅。
容斥原理
一道小学题 求 \(n(n\le 10^9)\) 以内不能被 \(2,3,5\) 整除的整数个数。
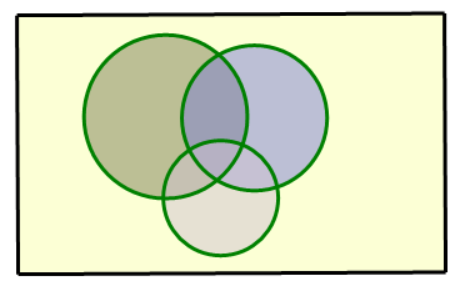
考虑这个 Venn 图。三个圆分别表示被 \(2,3,5\) 整除的数构成的集合，那么要求的就是圆外的面积。
假设什么限制也不管，只管一共有 \(n\) 个数，那么每块都是算一遍。
圆外的面积自然就是总面积减去里面的，我们想到 \(n-\lfloor \frac{n}{2}\rfloor-\lfloor \frac{n}{3}\rfloor-\lfloor \frac{n}{5}\rfloor\)。
你发现重合的部分多扣了，所以你又把两两的重合部分加上，现在你的答案是 \(n-\lfloor\frac{n}{2}\rfloor-\lfloor\frac{n}{3}\rfloor-\lfloor\frac{n}{5}\rfloor+\lfloor\frac{n}{2\times 3}\rfloor+\lfloor\frac{n}{2\times 5}\rfloor+\lfloor\frac{n}{3\times 5}\rfloor\)。
你发现中间（三圆重合的部分）又多出来了，把它减掉。\(n-\lfloor\frac{n}{2}\rfloor-\lfloor\frac{n}{3}\rfloor-\lfloor\frac{n}{5}\rfloor+\lfloor\frac{n}{2\times 3}\rfloor+\lfloor\frac{n}{2\times 5}\rfloor+\lfloor\frac{n}{3\times 5}\rfloor-\lfloor\frac{n}{2\times 3\times 5}\rfloor\)。
你发现它完美了：该算的被算了一遍，别的被算了零遍。
考虑一个比较一般的容斥的式子：
记 \(A_1\) 到 \(A_n\) 是 \(n\) 个集合，\(U=\{1,2,\cdots ,n\}\)。那么
为什么这是对的？
考虑一个元素。假设它出现在了 \(n\) 个集合中的 \(k(k>0)\) 个。则它的贡献恰好是
\(\sum_{i=1}^k (-1)^{i-1}\binom ki\\ =1-\sum_{i=0}^k (-1)^i\binom ki\\ =1-(-1+1)^k\\ =1\)
。我们发现有出现过的算了一次，没出现过的算了零次。
根据上面的经验，我们发现，容斥就是通过加加减减的方式，使得符合要求的方案算到恰好一遍，其他方案算到零遍，以做到不重不漏不多不少。
二项式反演
小学题加强版 对 \(k=0,1,2,3\)，分别求出 \(n(n\le 10^9)\) 以内恰能被 \(2,3,5\) 中的 \(k\) 个整除的整数个数。
先考虑 \(k=3\)，这时候答案显然是三圆重合的部分，就是 \(f_3=\lfloor\frac{n}{2\times 3\times 5}\rfloor\)。
然后是 \(k=2\)，这时我们想到 \(\lfloor\frac{n}{2\times 3}\rfloor+\lfloor\frac{n}{2\times 5}\rfloor+\lfloor\frac{n}{3\times 5}\rfloor\)。但是你发现中间那块被多算了 \(3\) 遍，于是有 \(f_2=\lfloor\frac{n}{2\times 3}\rfloor+\lfloor\frac{n}{2\times 5}\rfloor+\lfloor\frac{n}{3\times 5}\rfloor-\binom 32f_3\) 了。
接下来算 \(k=1\)，和刚才一样，你算出了 \(f_1=\lfloor\frac{n}{2}\rfloor+\lfloor\frac{n}{3}\rfloor+\lfloor\frac{n}{5}\rfloor-\binom 21f_2-\binom 31f_3\)。
那么 \(f_0=n-\binom 10f_1-\binom 20f_2-\binom 30f_3\)。
考虑比较一般的问题。你有 \(n\) 个限制，对所有的 \(k\)，要求出满足恰好 \(k\) 个限制的方案数。
对于一个 \(k\)，你强行钦定它满足其中 \(k\) 个条件，而算出答案为 \(g_k\)；记最后的答案为 \(f_k\)。那么根据刚才的经验，很明显：
但这个复杂度是 \(n^2\) 的，有时候 \(n\) 很大，你算不了。有没有更快的做法？
那你移个项，容易得到：\(g_k=\sum_{j=k}^n\binom jk f_j\)。
组合数拆出来：\(k!g_k=\sum_{j=k}^n \frac{1}{(j-k)!}j!f_j\)
设 \(g'_k=g_{n-k}(n-k)!,f'_k=f_{n-k}(n-k)!\)。那么 \(g'_k=\sum_{j=0}^k\frac{1}{(k-j)!}f'_j\)。
然后是喜闻乐见的生成函数环节。\(G_1(x)=\sum_i g'_ix^i,F_1(x)=\sum_i f'_ix^i\)。
那么就有 \(G_1(x)=e^xF_1(x)\)。所以 \(F_1(x)=e^{-x}G_1(x)\)。而 \(e^{-x}=\sum_i (-1)^i\frac{x^i}{i!}\)。
这时候我们就有了明显的思路：先从 \(g\) 数组转成 \(G_1(x)\)，然后使用 FFT/NTT 做卷积，算出 \(F_1(x)\)，然后转成 \(f\) 数组。
时间复杂度 \(O(n\log n)\)。
但是有时候我们不仅想这样求，还想把式子给他写得漂亮些。
刚刚我们推到了 \(F_1(x)=e^{-x}G_1(x)\)，其中 \(e^{-x}=\sum_i (-1)^i\frac{x^i}{i!}\)。
也就是 \(f'_k=\sum_{j=0}^k\frac{(-1)^{k-j}}{(k-j)!}g'_j\)。
\(k!f_k=\sum_{j=k}^n\frac{(-1)^{j-k}}{(j-k)!}j!g_j\)
\(f_k=\sum_{j=k}^n\binom jk(-1)^{k-j}g_j\)。事实上啊，
这个式子就是二项式反演了。二项式反演还有更好看的形式：
min-max 容斥
再看看这个容斥的式子：
记 \(A_1\) 到 \(A_n\) 是 \(n\) 个集合，\(U=\{1,2,\cdots ,n\}\)。那么\(
|\bigcup_{i=1}^n A_i|=\sum_{S\subset U,S\ne \emptyset}(-1)^{|S|-1}|\bigcap_{i\in S}A_i|
\)。
试试把 \(\bigcup\) 换成 \(\max\)，把 \(\bigcap\) 换成 \(\min\)，集合 \(A_i\) 改成数 \(a_i\) 吧。那么得到：
举个例子：
\(
\max\{2,3,4\}\\
=\min\{2\}+\min\{3\}+\min\{4\}-\min\{2,3\}-\min\{2,4\}-\min\{3,4\}+\min\{2,3,4\}\\
=2+3+4-2-2-3+2
=4
\)
你发现它竟然是对的！
能证明吗？
一样的思路，不妨假设 \(a_1\le a_2\le \cdots\le a_n\)。考虑 \(a_x\) 被算到的次数，为：
\(\sum_{i=0}^{n-x}\binom {n-x}i (-1)^{n-x}\)
（它要是子集的最小值，该子集的其他元素就只能选后面的）。
当 \(k<n\) 时，化为 \((-1+1)^{n-k}=0\)；当 \(k=n\) 时，化为 \(1\)。
故只有最大的那个值贡献到了答案，它就是对的。这就是 min-max 容斥。
但是你觉得这个东西很蠢，最大值明明可以直接算。
之所以要拿出来说，是因为 min-max 容斥在期望下也是对的。
也就是说，
成立。
举例说明：袋子里有 \(n(n\le 20)\) 种颜色的球，每一回合你会拿出一个球然后放回，摸出的球为第 \(i\) 种颜色的概率为 \(p_i(\sum p_i=1)\)。求期望多少回合后，每种颜色都摸到过至少一次。（HDU4336）
设第 \(i\) 种颜色期望 \(x_i\) 次被第一次摸到，则答案是 \(E(\max_{i=1}^n x_i)\)。
你发现 \(E(\max x_i)\) 不好求，\(E(\min_{i\in S}x_i)\) 还比较好求，为 \(\frac{1}{\sum_{i\in S} p_i}\)。
套用刚刚的式子，就得到
\(
E(\max_{i=1}^n x_i)\\
=\sum_{S\subset U,S\ne \emptyset}(-1)^{|S|-1}E(\min_{i\in S}x_i)\\
=\sum_{S\subset U,S\ne \emptyset}(-1)^{|S|-1}\frac{1}{\sum_{i\in S} p_i}
\)
\(n\) 只有 \(20\)，直接算就行了。
Wait! 但是我们还没证明 min-max 容斥在期望下也是对的呢！
考虑在这里计算期望的一种方法：
\(E(\max_{i=1}^n x_i)=\sum_tP(x=t)\max_{i=1}^n t_i\)
\(E(\min_{i=1}^n x_i)=\sum_tP(x=t)\min_{i=1}^n t_i\)
其中 \(t\) 是一个长度为 \(n\) 的序列。
\(E(\max_{i=1}^n x_i)\\ =\sum_tP(x=t)\max_{i=1}^n t_i\\ =\sum_tP(x=t)\sum_{S\subset U,S\ne \emptyset}(-1)^{|S|-1}\min_{i\in S}t_i\\ =\sum_{S\subset U,S\ne \emptyset}(-1)^{|S|-1}\sum_tP(x=t)\min_{i\in S}t_i\\ =\sum_{S\subset U,S\ne \emptyset}(-1)^{|S|-1}E(\min_{i\in S}x_i) \)
嗯，这样就证完了，也没啥意思。
还有更强的式子
记 \(U=\{1,2,\cdots ,n\}\)，\(\operatorname{kthmax}_{i=1}^n a_i\) 为 \(a\) 数组的第 \(k\) 大值，则：
（规定 \(n<m\) 时 \(\binom nm=0\)）
证明：
不妨假设 \(a_1\le a_2\le \cdots\le a_n\)。
\(\sum_{S\subset U,S\ne \emptyset}(-1)^{|S|-k}\binom{|S|-1}{k-1}\min_{i\in S}a_i\\
=\sum_{i=1}^n a_i\sum_{S\subset U,S\ne \emptyset}(-1)^{|S|-k}\binom{|S|-1}{k-1}[a_i=\min_{j\in S}a_j]\\
=\sum_{i=1}^n a_i\sum_{j=k}^n\binom{n-i}{j-1}\binom{j-1}{k-1}(-1)^{j-k}\)
对于组合数，有等式 \(\binom ab\binom bc=\binom ac\binom{a-c}{b-c}\)。于是：
\(
=\sum_{i=1}^n a_i\sum_{j=k}^n\binom{n-i}{k-1}\binom{n-i-k+1}{j-k}(-1)^{j-k}\\
=\sum_{i=1}^n a_i\binom{n-i}{k-1}\sum_{j=k}^n\binom{n-k+1-i}{j-k}(-1)^{j-k}\\
=\sum_{i=1}^n a_i\binom{n-i}{k-1}\sum_{j=0}^{n-k+1-i}\binom{n-k+1-i}{j}(-1)^{j}
\)
当 \(i=n-k+1\) 时，\(\binom{n-i}{k-1}\sum_{j=0}^{n-k+1-i}\binom{n-k+1-i}{j}(-1)^{j}=1\)；
否则 \(\binom{n-i}{k-1}\sum_{j=0}^{n-k+1-i}\binom{n-k+1-i}{j}(-1)^{j}=0\)。
所以 \(\sum_{i=1}^n a_i\binom{n-i}{k-1}\sum_{j=0}^{n-k+1-i}\binom{n-k+1-i}{j}(-1)^{j}=\operatorname{kthmax}_{i=1}^n a_i\)
于是证完了。
于是又有
EXTRA
其实还有一个关于 \(\gcd\) 和 \(\operatorname{lcm}\) 的容斥。
它长这样：\(\operatorname{lcm}_{i=1}^n a_i=\prod_{S\subset U,S\ne \emptyset}(\gcd_{i\in S}a_i)^{(-1)^{|S|-1}}\)
其中 \(U=\{1,2,\cdots ,n\}\)。
为什么对？你考虑 \(a_i=\prod_k p_k^{\alpha_k}\)。
- 取两个数的 \(\gcd\) 就是每个 \(\alpha\) 取 \(\min\)；
- 取两个数的 \(\operatorname{lcm}\) 就是每个 \(\alpha\) 取 \(\max\)；
- 两个数相乘就是 每个 \(\alpha\) 求和；
- 两个数相除就是 每个 \(\alpha\) 求差。
于是那个式子就相当于对每个 \(\alpha\) 同时搞了个 min-max 容斥，自然就是对的了。
例题
二项式反演
luogu P4859 已经没有什么好害怕的了
luogu P4491 染色
luogu P5401 珍珠
min-max 容斥
HDU 4336 Card Collector
luogu P3175 按位或
HDU4624 Endless Spin
BZOJ 4833 最小公倍佩尔数
luogu P4707 重返现世
AGC 038E Gachapon
