POI2011 Lightning Conductor

题目

这阵子学二分队列，写个题解吧。

要对每个 \(i\)，求出最小非负整数 \(p\) ，使得 \(\forall j\in[1,n],a_j\le a_i+p−\sqrt{|i−j|}​\)。

那么 \(a_i+p\ge \max\{\max_{j<i}a_j+\sqrt{i-j},\max_{j>i}a_j+\sqrt{j-i}\}\)

求出大于等于号右边的东西即可。考虑求出 \(\max_{j<i}a_j+\sqrt{i-j}\)。（\(j>i\) 的东西类似做就好）

把 \(a_j+\sqrt{i-j}\) 看作以 \(i\) 为自变量的函数，对于所有 \(j<i\)，所有函数值的最大值就是要求的。

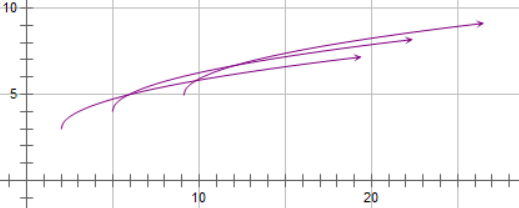
这些函数的图像画在一起，大概长这样。

考虑其中的一个函数，在 \(i\) 增大的过程中，或者是从始至终被吊打，或者是开始时不如别人，中间吊打所有人，最后又被超过，然后永世不得翻身。

为什么永世不得翻身？因为这里面所有的函数都是增长越来越慢（大概是取值范围内导数小于零）的，考虑 后面的函数 超过 前面的函数 的时候，后面的函数 的增长就比 前面的函数 快，在这之后 后面的函数 还是一直比 前面的函数 快，所以 前面的函数 在此之后不会再出头。

根据这个性质，考虑维护一个队列，队列里面是一堆函数（设为 \(f_1,f_2,\cdots,f_d\)），且\(\forall k ,f_k\) 超过 \(f_{k-1}\) 的时间要早于 \(f_{k+1}\) 超过 \(f_k\) 的时间。

（以下认为队尾进队头出。）

当拿到一个新函数的时候，和队尾的函数求一下交（可以二分，本题似乎也可以直接解方程），如果永远超不过队尾就扔掉；如果新函数与队尾的相交的时间晚于队尾两个函数相交的时间，就直接塞入队尾，否则一直弹队尾直到可以为止。

当你要求答案的时候，不断弹队首，直到找到需要的即可。

从前往后做一遍就求出答案了。（可以看代码，关键部分是 Solve 函数。）

#include<cstdio>
#include<algorithm>
#include<cmath>
const int N=5e5+3;
int n,a[N],b[N],s[N],t[N],q[N],f[N],l,r;
inline int Calc(int i,int j,int*a){//求交点的函数
	int l=j+1,r=n+1,m;
	for(;l<r;)m=l+r>>1,a[i]+sqrt(m-i)<a[j]+sqrt(m-j)?r=m:l=m+1;
	return l;
}
inline int Solve(int*a,int*s){
	int tmp;
	q[l=r=0]=1;
	for(int i=2;i<=n;i++){
	  for(;l<r&&f[l+1]<=i;l++);//弹队首
	  s[i]=a[q[l]]+ceil(sqrt(i-q[l]));//求答案
	  for(;l<r&&Calc(q[r],i,a)<f[r];r--);//弹队尾
	  if((tmp=Calc(q[r],i,a))<=n)q[++r]=i,f[r]=tmp;//加入新函数
	}
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d",a+i),b[n-i+1]=a[i];
	Solve(a,s);
	Solve(b,t);
	for(int i=1;i<=n;i++)
	  printf("%d\n",std::max(s[i],t[n-i+1])-a[i]>0?std::max(s[i],t[n-i+1])-a[i]:0);
	return 0;
}