笛卡尔树学习笔记
笛卡尔树是一种二叉树,一个序列 a[l:r] 的笛卡尔树大概是这样定义的:
-
找到最小元素(设为
a[i])作为树的根; -
根的左子树是序列
a[l:i-1]的笛卡尔树,右子树是序列a[i+1:r]的笛卡尔树。
当然,对于相等的最小元素,选哪个为根都行。举例如下:
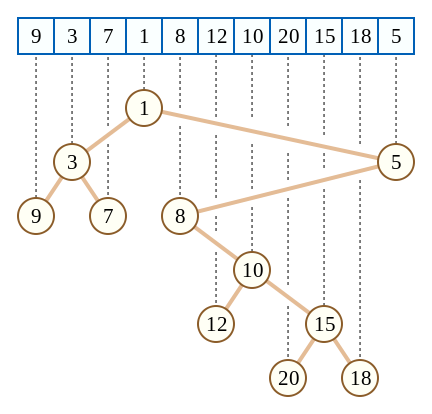
其中序遍历就是原序列,并且其点权有小根堆的性质,两点之间的最小值就是 LCA 上的值。
笛卡尔树有一种 \(O(n)\) 的构建方法,基于单调栈。
大概是从前往后扫,扫到一个元素 \(a_i\) 的时候,利用单调栈找到它之前的第一个比它小的 \(a_j\)。
-
如果 \(j\) 已经有了右儿子 \(k\) ,那么 \(k\) 变成 \(i\) 的左儿子,然后再将 \(i\) 设为 \(j\) 的右儿子。
-
否则直接将 \(i\) 设为 \(j\) 的右儿子。
然后你就造完了一棵笛卡尔树。
有什么用?
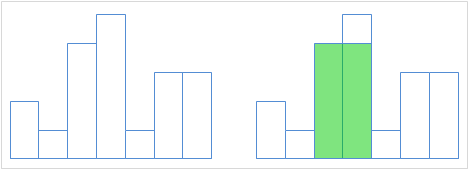
例.如上图,给出 \(n\) 和从左往右每根柱的高度,求其包含的最大矩形。\(n\le 2\times 10^6\)。
单调栈可以直接做,但是不重要。
建出笛卡尔树,求出其所有子树中,子树大小乘高度的最大值就是答案,复杂度 \(O(n)\)。
一些题目
SP3734 PERIODNI - Periodni
IOI2018 meetings
还有一些不知道从哪里搜集来的杂题:
1.刚开始你有 \(𝑛\) 个序列,刚开始序列都是长度为 \(1\) 的。每次要你拼接两个序列,问每个序列的每个子区间的最小值的和。\(𝑛 ≤ 10^6\)。
2.给出 \(n\),随机一个 \(1\) 到 \(n\) 的排列 \({P_n}\),求 \(\sum_{i=2}^n|P_i-P_{i-1}|\) 的期望,对大质数取模。\(n\le 100\)。



