APIO2009 采油区域

挺好玩的一题。

题目

题意：从 \(N\times M\) 的矩阵中选出 \(3\) 个互不相交的 \(K\times K\) 的正方形，使它们所包含数的和最大。

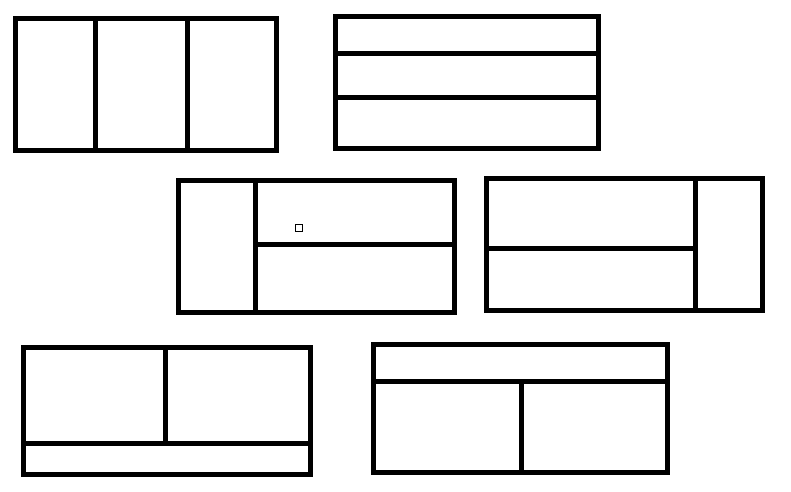
用上图的六种切法把大矩阵切开，则其中必有一种切法使选出的 \(3\) 个正方形分别在切出的 \(3\) 个部分里。

前缀和维护即可。

#include<cstdio>
#define max(a,b)((a)>(b)?(a):(b))
const int N=1502;
int n,m,k,a[N][N],b0[N][N],b1[N][N],b2[N][N],b3[N][N],c0[N],c1[N],ans,tmp;
int main(){
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)
	  scanf("%d",&a[i][j]),a[i][j]+=a[i-1][j]-a[i-1][j-1]+a[i][j-1];
	for(int i=n;i>=k;i--)for(int j=m;j>=k;j--)
	  a[i][j]-=a[i][j-k]-a[i-k][j-k]+a[i-k][j],
	  c0[i]=max(c0[i],a[i][j]),
	  c1[j]=max(c1[j],a[i][j]);
	for(int i=k;i<=n;i++)for(int j=k;j<=m;j++)
	  b0[i][j]=max(max(b0[i-1][j],b0[i][j-1]),a[i][j]);
	for(int i=k;i<=n;i++)for(int j=m;j>=k;j--)
	  b1[i][j]=max(max(b1[i-1][j],b1[i][j+1]),a[i][j]);
	for(int i=n;i>=k;i--)for(int j=k;j<=m;j++)
	  b2[i][j]=max(max(b2[i+1][j],b2[i][j-1]),a[i][j]);
	for(int i=n;i>=k;i--)for(int j=m;j>=k;j--)
	  b3[i][j]=max(max(b3[i+1][j],b3[i][j+1]),a[i][j]);
	for(int i=k;i+k<=n;i++)for(int j=k;j+k<=m;j++)
	  ans=max(ans,b0[i][j]+b1[i][j+k]+b3[i+k][k]),
	  ans=max(ans,b1[i][j+k]+b3[i+k][j+k]+b0[n][j]),
	  ans=max(ans,b3[i+k][j+k]+b2[i+k][j]+b0[i][m]),
	  ans=max(ans,b2[i+k][j]+b0[i][j]+b3[k][j+k]);
	for(int i=k;i+k+k<=n;i++){
	  tmp=0;
	  for(int j=i+k;j+k<=n;j++)
		tmp=max(tmp,c0[j]),
		ans=max(ans,b0[i][m]+b3[j+k][k]+tmp);
	}
	for(int i=k;i+k+k<=m;i++){
	  tmp=0;
	  for(int j=i+k;j+k<=m;j++)
		tmp=max(tmp,c1[j]),
		ans=max(ans,b0[n][i]+b3[k][j+k]+tmp);
	}
	printf("%d",ans);
	return 0;
}