[笔记] LCT 入门

其实可能是从零开始的复习，多年不会 LCT 人在 NOI 延期一个月，为了改模拟考试 t1 后，终于决定重学 LCT。

感性理解 LCT#

LCT 是动态树的一种，它可以支持一些动态的树相关的操作。

比如维护一个森林，支持删除某条边，加入某条边，并保证加边，删边之后仍是森林。

要维护这个森林的一些信息，一般的操作有两点连通性，两点路径权值和，连接两点和切断某条边、修改信息等。

可以简单的把 LCT 理解成用一些 splay 来维护动态的树链剖分，以实现动态树上的区间操作。

对于每条实链，我们建一个 splay 来维护整个链区间的信息，可以认为一些 splay 构成了一个辅助树，每棵辅助树维护的是一棵树，一些辅助树构成了 LCT，其维护的是整个森林。

感性理解辅助树#

• 辅助树的每棵 splay 维护原树中的一条路径，中序遍历这棵 splay 得到的序列，从前到后对应原树 “从上到下” 的一条路径，即以深度为关键字的二叉搜索树。

• 原树每个节点与辅助树的 splay 节点一一对应。

• 辅助树的各棵 splay 之间并不是独立的，splay 的根节点的父亲节点一般为空，但在 LCT 中 splay 根节点的父亲节点指向原树中 这条链 的父亲。

  但是这类父亲链接与通常 splay 的父亲链接又有区别，它是认父不认子的，对应原树的一条 虚边。

  所以，每个连通块仅有恰好一个节点的父亲为空。

• 辅助树可以在任何情况下拿出一个唯一的原树。

基本函数#

rotate(x)：通过旋转，使得节点 x 向上一层。#

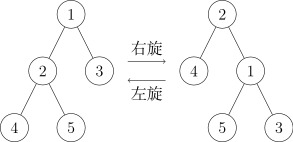
具体操作细节一般通过想象操作结果来实现。

void rotate(int x){
    int y = fa[x], p = Get(x);
    fa[x] = fa[y]; if(!is_rt(y)) ch[fa[y]][Get(y)] = x;
    ch[y][p] = ch[x][!p]; if(ch[x][!p]) fa[ch[x][!p]] = y;
    ch[x][!p] = y, fa[y] = x;
    pushup(y), pushup(x);
}

splay(x)：将节点 x 旋转为当前 splay 的根#

注意 update 下放标记，以及到底是旋 x 还是其父亲。

void splay(int x){
    update(x);
    for(int y = fa[x]; !is_rt(x); rotate(x), y = fa[x])
        if(!is_rt(y)) rotate(Get(x) == Get(y) ? y : x);
}

access(x)：将节点 x 到根的路径置为同一棵 splay#

void access(int x){
    for(int y = 0; x; y = x, x = fa[x]) splay(x), rs(x) = y, pushup(x);
}

makert(x)：将树的根换成节点 x#

是通过将 x 节点到根的整条路径在深度上翻转实现的。

void makert(int x){
    access(x), splay(x), rev(x);
}

findrt(x)：找到节点 x 所在树的根#

int findrt(int x){
    access(x), splay(x);
    while(ls(x)) pushdown(x), x = ls(x);
    splay(x); return x;
}

split(x,y)：使得节点 x，y 所在 splay 刚好是这条路径上的所有点#

void split(int x, int y){
    makert(x), access(y), splay(y);
}

link(x,y)：将节点 x 连一条指向节点 y 的边#

void link(int x, int y){
    makert(x), fa[x] = y;
}

cut(x)：将节点 x，y 之间的边切断#

void cut(int x, int y){
    split(x, y), fa[x] = ch[y][0] = 0, pushup(y);
}

其他次要函数#

inline bool is_rt(int x){ return ls(fa[x]) != x && rs(fa[x]) != x; }
inline bool Get(int x){ return rs(fa[x]) == x; }
inline void rev(int x){ if(!x) return; swap(ls(x), rs(x)), rv[x] ^= 1; }
inline void pushup(int x){ 
	siz[x] = siz[ls(x)] + 1 + siz[rs(x)];
	sum[x] = sum[ls(x)] ^ val[x] ^ sum[rs(x)];
}
inline void pushdown(int x){ if(rv[x]) rev(ls(x)), rev(rs(x)), rv[x] = 0; }
void update(int x){
	if(!is_rt(x)) update(fa[x]);
	pushdown(x);
}
void modify(int x, int v){
	splay(x), val[x] = v, pushup(x);
}

实现细节#

• 因为 LCT 是认父不认子，所以注意对于一个节点是否为 splay 的根的判断方法。
• 支持 cut 时，如果不保证合法，应判断两点在同一子树，且 split 后，splay 大小为 2。
• 时刻注意是否需要 pushup，pushdown 等。

相关应用#

LCT 维护子树信息#

LCT 一般维护的是一条链上的信息，那么如何使其维护子树信息呢?

方法是对于每个节点，再用一个变量维护其所有虚儿子的信息和，那么有哪些操作会受影响呢?

void pushup(int x){
    siz[x] = siz[ls(x)] + 1 + siz[rs(x)] + si[x];
}
void access(int x){
    int lst_val = 0;
    for(int y = x; x; y = x, x = fa[x]){
        splay(x), vali[x] += val[rs(x)] - lst_val, lst_val = val[x], rs(x) = y, pushup(x);
    }// 存 lst_val 的原因是因为维护有的值会被 pushup 影响，就不是原来要减去的那个了。
}
void link(int x, int y){// notice makert(y) !!!
    makert(x), makert(y), fa[x] = y, si[y] += siz[x];
}

即所有对树上虚实边有影响的操作，都需要考虑对虚儿子信息的影响。

一般来说维护的信息要有 可减性 (而链维护的信息只要可加性)，如子树结点数，子树权值和，否则比如维护节点最值，可能每个节点要开一棵平衡树维护子节点权值。

LCT 维护边权#

LCT 上没有固定的父子关系，所以不方便将边权记录在点权中。

所以可以 拆边。对每条边建立一个对应点，从这条边向其两个端点连接一条边，原先的连边与删边操作都变成两次操作。