[笔记] 卡特兰数

同步发表于 MiNa!

基础知识

卡特兰数的式子

\[\begin{aligned} &h(n)=\sum_{i=0}^{n-1}h(i)\cdot h(n-i-1)\\ &h(n)=\frac{h(n-1)\cdot(4n-2)}{n+1}\\ &h(n)=\frac{\binom{2n}{n}}{n+1}=\frac{\binom{2n+1}{n}}{2n+1} \end{aligned} \]

卡特兰数的例子

• 合法出栈入栈操作序列。
• 合法括号序列。
• 凸多边形划分为三角形的方案数。

拓展

广义卡特兰数

似乎网上有相关论文，此处仅提及 FJOI 2020 D2T2 题目的例子浅显地了解一下。

将 \(m\) 边凸多边形划分为 \(n\) 个 \(k\) 边形的方案 ( \(m=nk-2(n-1)\) )

可以推导递推式

\[h(n)=\sum_{S}\prod_{x\in S} h(x)\ [\ |S|=k-1,\sum_{x\in S}x=n-1] \]

也可以用生成函数表示

\[H(n)=xH^{k-1}(n)+1 \]

还可以将划分方案映射为序列

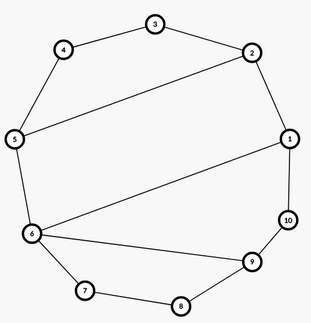
我们以十边形划分为 \(4\) 个四边形为例，给出映射的规则：

从 \(1\) 号点出发，依次遍历所有顶点，每抵达一个顶点，记为 \(+1\)，若当前顶点有指向编号更小的顶点的弦，则把划分出的一块全部割掉，那么此时边数的变化是减少了 \(k-1\) 条边，然后增加了当前弦这一条边，故记为 \(-(k-2)\)。

特别的，我们把 \(n\) 与 \(1\) 的连边看作弦处理。

那么一个合法的划分方案将映射为一个由 \(n\) 个 \(-(k-2)\)，\(nk-2n+1\) 个 \(+1\) 组成的前缀和为正的序列。

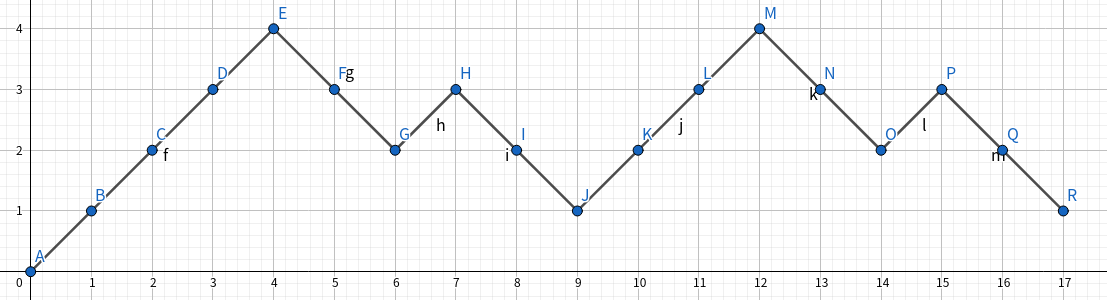
直接由 Raney 引理 得到方案数为 \(\dfrac{\binom{nk-n+1}{n}}{nk-n+1}\).

Raney 引理

一个环 \(x_1,x_2,...,x_n\)，满足 \(∑x_i=1\)，在将它裂开形成的 \(n\) 条可能的链中，恰有一条满足所有前缀和都是正数。

可以用于推导卡特兰数的一个通项式 \(\dfrac{\binom{2n+1}{n}}{2n+1}\).

首先卡特兰数的等价于一个长为 \(2n\)，由 \(n\) 个 \(1\) 和 \(n\) 个 \(-1\) 组成前缀和非负的序列的方案数。

加入一个 \(1\) 使得 \(2n+1\) 个数的和是 \(1\)，以使用 Raney 引理。

首先这 \(2n+1\) 个数的排列方案是 \(\binom{2n+1}{n}\)，而由引理可知，每 \(2n+1\) 个循环同构的排列方式只有 \(1\) 种合法。

故方案数为 \(\dfrac{\binom{2n+1}{n}}{2n+1}\)，然后因为加入一个 \(1\) 新序列要求所有前缀和为正，所以序列首一定是 \(1\)，那么和满足卡特兰数含义的序列其实就是一一对应的。