[笔记] 建图
最小割
模型概述1
有 \(n\) 个物品和两个集合 \(A,B\) ，如果将一个物品放入 \(A\) 集合会花费 \(a_i\)，放入 \(B\) 集合会花费 \(b_i\)。
还有若干个形如 \((u_i,v_i,w_i)\) 限制条件，表示如果 \(u_i\) 和 \(v_i\) 不在一个集合会花费 \(w_i\)。
每个物品必须且只能属于一个集合，求最小的代价。
建图：
是一个经典的 二者选其一 的最小割题目。我们对于设置源点 \(s\) 为 \(A\) 集合，汇点 \(t\) 为 \(B\) 集合。
第 \(i\) 个点由 \(s\) 连一条容量为 \(a_i\) 的边、向 \(t\) 连一条容量为 \(b_i\) 的边。
对于限制条件 \((u_i,v_i,w_i)\) ，在 \(u_i,v_i\) 之间连容量为 \(w_i\) 的双向边。
费用流
模型概述1
一个长度为 \(n\) 的序列 \(a_i\)，对于区间 \([l,r]\) 减一的费用为 \(c_{i,0}\)，加 \(1\) 的费用为 \(c_{i,1}\)，问最少使 \(a_i\) 都变为 \(0\) 的费用。
建图概述
差分之后，相当于对某一对单点的加减，按照最终需要的结果算出每个位置的需要加减权值。
将 \(T\) 连正权，负权连 \(S\)，中间的连边按照代价连。
习题
[YZOJ] 7087 pandemic \(√\)
[DMOJ] DMOPC '20 Contest 7 P3 Senpai and Art \(√\)
模型概述2
\(S\) 到 \(T\) 有 \(n\) 条链，每条链 \(m_i\) 条边，记第 \(i\) 条链的第 \(j\) 条边为 \((i,j)\)，切断的代价为 \(v_{i,j}\)。
同时有 \(q\) 个限制 \((x_i,a_i,y_i,b_i)\)，表示如果第 \(x_i\) 条链割的边不小于 \(a_i\)，则第 \(y_i\) 条链割的边不小于 \(b_i\)。
求合法最小割。
建图概述
感性理解就是 \((x_,i)\) 向 \((y,j)\) 连一条边表示 \(x\) 割的边在 \(i\) 以后，则 \(y\) 必须割 \(j\) 以后的边，才能分开 \(S,T\)。
如果是最大化代价，用 \(\infty-v_{i,j}\) 建图即可。
习题
[P6054] [RC-02] 开门大吉 \(√\)
[P3227] [HNOI2013]切糕 \(√\)
[BZOJ4657] tower \(√\)
模型概述2 (最小路径覆盖)
给出 \(n\) 个点，要求第 \(i\) 个点经过 \(a_i\) 次，经过 \(i\) 之后选择走 \(j\) 的代价是 \(p_{i,j}\)，询问代价最值的问题。
建图概述
这个问题相当于在图上选择符合要求的若干条路径。
考虑到每个点的经过次数是固定的，实际上并不关心每条路径的整个走向，而只关心每条路径的相邻两点到底是谁走向谁。
不妨把每个点拆成 \(i,i'\)，然后连边 \({\rm add}(S\ , i\ , a_i\ ,0)\ ,{\rm add}(i'\ ,T\ ,a_i\ ,0)\ ,{\rm add}(i\ ,j'\ ,\infty\ , p_{i,j})\).
特殊的，如果每个点的经过次数只有下限没有上限，再 \({\rm add}(i'\ ,i\ ,\infty\ ,0)\).
习题
P4298 [CTSC2008]祭祀
P4553 80人环游世界 \(√\)
P1251 餐巾计划问题 \(√\)
P2469 [SDOI2010]星际竞速
P4043 [AHOI2014/JSOI2014]支线剧情
优化建图
虚点优化建图
由若干完全子图构成的图的最大匹配问题
考虑优化建图。对于每个完全子图，建 \(k\) 个辅助点，连边如下图：
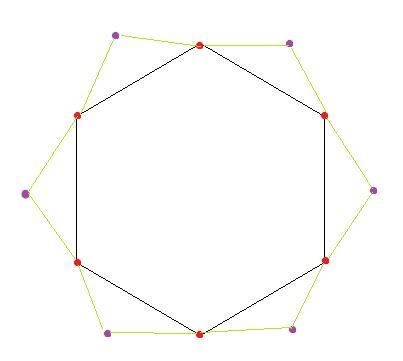
红点是辅助点，紫点是原图的点。即辅助点连成一个环，原来的点插在相邻的两个辅助点中间。
容易归纳证明当紫点还有 \(x\) 个可用时，最大匹配是 \(\lfloor\frac{x+k}{2}\rfloor\)。只需取一个偶数的 \(k\) 然后减去 \(\frac{k}{2}\) 即可。
这样我们就把边数降到了若干子图大小和的级别。
- 前缀和优化建图
- 线段树优化建图
