动态dp
以前学树型dp留下的题目,没有写,然后过了几个月后又回来写了这道题
战略游戏
这是一道典型的最小点覆盖的模板,蒟蒻采用的是树型dp的做法
设 \(f[i][0/1]\) 在以 \(i\) 为根的子树中,选或不选当前这个点所需要的最少的点
那么转移方程为:
\(f[i][0]=\sum_{v\in son[i]} f[v][1]\)
\(f[i][1]=\sum_{v\in son[i]} min(f[v][0],f[v][1])+1\)
图片解释:
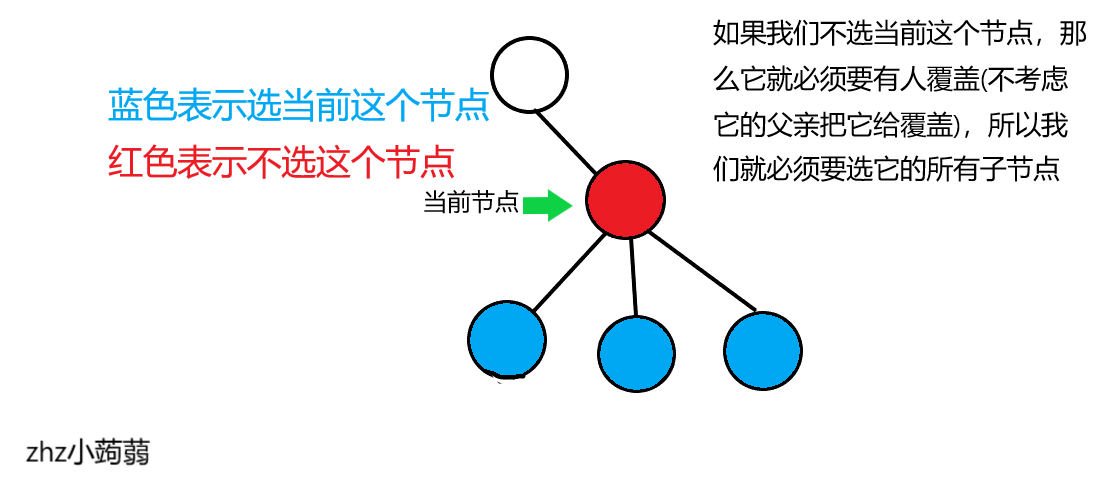
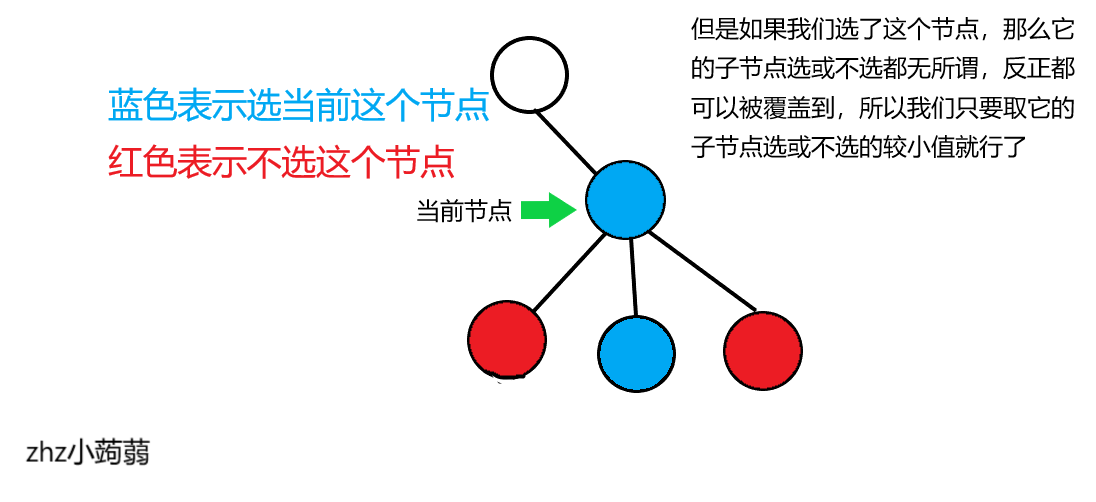
然后我们从根节点开始,\(dfs\) 遍历每一个节点,然后在每次遍历完一个节点后进行一次树型 \(dp\) ,注意,这个过程是从叶子结点到根的。
\(Code:\)
#include <iostream>
#include <cstdio>
using namespace std;
struct Node
{
int t;
int next;
}node[30011];
int n,tot;
int f[3011][2],head[3011];
void add(int x,int y)
{
node[++tot].t=y;
node[tot].next=head[x];
head[x]=tot;
return;
}
void dfs(int u,int fa)
{
f[u][1]=1; //f[u][1]要初始化为1,因为它要选上自己这个点
for(int i=head[u];i;i=node[i].next)
{
int v=node[i].t;
if(v!=fa)
{
dfs(v,u);
f[u][0]+=f[v][1]; //如上面的转移方程
f[u][1]+=min(f[v][1],f[v][0]);
}
}
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
int step;
scanf("%d",&step);
++step;
int k;
scanf("%d",&k);
for(int j=1;j<=k;++j)
{
int y;
scanf("%d",&y);
++y;
add(step,y);
add(y,step); //因为题目中的标号是0~n-1,我为了方便就将每个节点加了1
}
}
dfs(1,0);
printf("%d",min(f[1][0],f[1][1]));
return 0;
}
但是,如果我们加上一个修改操作,每一次都进行修改,然后询问 \(dp\)值,这应该怎么做呢?
这就需要用到我们的标题:动态\(dp\) 了。
动态dp
这道题目要求的是最大点权独立集权值,我们把上面的方程稍微改一下,注意,是独立集,不是覆盖集
\(f[i][0]=\sum_{v\in son[i]} max(f[v][0],f[v][1])\)
\(f[i][1]=\sum_{v\in son[i]} f[v][0]+a[i]\)
图片解释:
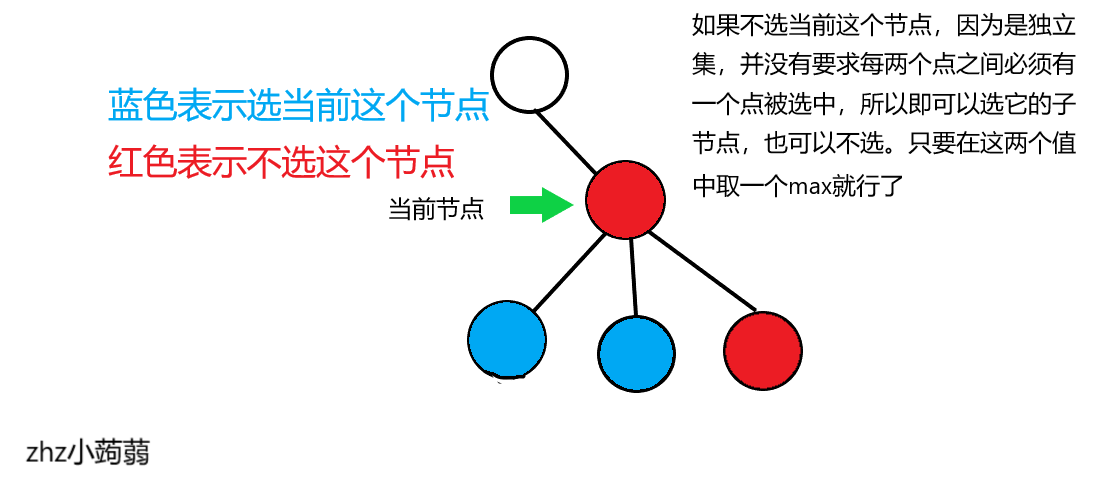
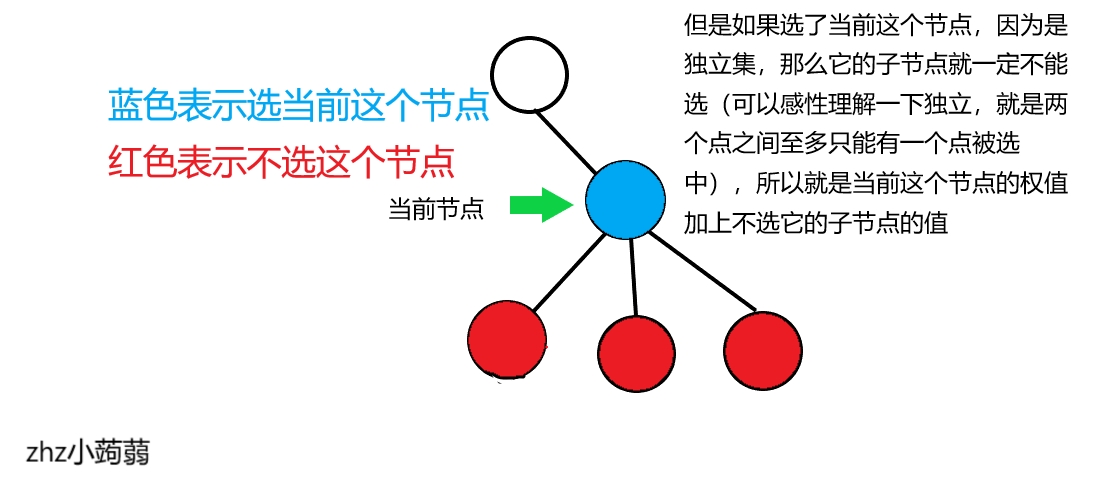
注:\(a[i]\) 表示节点 \(i\) 的权值
我们首先回想一下矩阵乘法的式子:
\(C_{i,j}=\sum_{k=1}^{p}A_{i,k}* B_{k,j}\)
然后我们来脑补一下\(floyd\) 的转移方程:
\(f_{i,j}=min_{k=1}^{n}f_{i,k}+f_{k,j}\)
嗯,为什么看起来这么相似呢?
好像只是把\(\sum\) 换成了\(min\) ,$* $ 改成了 \(+\) 啊,这样子的矩阵乘法是对的吗?
答案是 \(YES\)
这时候我们就可以想到一种方法,我们能不能把转移方程改写成这种新定义的矩阵乘法的形式,然后用线段树来维护一段区间的矩阵乘法的乘积,从而实现 \(nlogn\) 的时间复杂度呢?
答案是 \(Right!\)
但是,我们上面的转移方程不好直接写成矩阵乘法的形式,我们将它改变一下:
设 \(g[i][0/1]\) 表示不包含\(i\)处在的重链上的节点(包括 \(i\))
\(g[i][0]=\sum_{v\neq son[i]} max(f[v][0],f[v][1])\)
\(g[i][1]=\sum_{v\neq son[i]} f[v][0]+a[i]\)
那么原来的转移方程就可以改为:
\(f[i][0]=g[x][0]+max(f[son[i][0],f[son[i]][1])\)
$f[i][1]=g[x][1]+f[son[i][0] $
改写成矩阵乘法的形式就是:
这里我用的是 \(LCT\) 的写法,复杂度为 \(mlogn\) ,当然也有树链剖分的写法,复杂度为 \(mlog^2n\)
\(Code:\)
#include <iostream>
#include <cstdio>
#define inf 1<<30
#define R register int
#define I inline void
#define lc c[x][0]
#define rc c[x][1]
#define N 100011
using namespace std;
struct Matrix
{
long long data[2][2];
Matrix()
{
data[0][0]=data[0][1]=data[1][0]=data[1][1]=-inf;
}
};
struct Node
{
int t;
int next;
}node[N<<1];
int a[N],f[N],c[N][2],head[N],dp[N][2],st[N];
Matrix val[N],prd[N];
int n,m,tot=0;
I add(int x,int y)
{
node[++tot].t=y;
node[tot].next=head[x];
head[x]=tot;
}
inline Matrix mul(const Matrix &A,const Matrix &B)
{
Matrix C;
for(int k=0;k<=1;++k)
for(int i=0;i<=1;++i)
for(int j=0;j<=1;++j)
C.data[i][j]=max(C.data[i][j],A.data[i][k]+B.data[k][j]); //注意,这里的矩阵乘法是重定义后的
return C;
}
inline bool nroot(R x)
{
return (c[f[x]][0]==x)||(c[f[x]][1]==x);
}
inline int chk(R x)
{
return c[f[x]][1]==x;
}
I pushup(R x)
{
prd[x]=val[x];
if(c[x][0]) prd[x]=mul(prd[c[x][0]],prd[x]);
if(c[x][1]) prd[x]=mul(prd[x],prd[c[x][1]]);
}
I rotate(R x)
{
R y=f[x],z=f[y],d=chk(x)^1,w=c[x][d];
if(nroot(y)) c[z][chk(y)]=x;
c[x][d]=y; c[y][d^1]=w;
if(w) f[w]=y;
f[x]=z; f[y]=x;
pushup(y); pushup(x);
return;
}
I splay(R x)
{
R y=x,z=0;
while(nroot(x))
{
y=f[x];z=f[y];
if(nroot(y))
rotate((c[z][0]==y)^(c[y][0]==x)?y:x);
rotate(x);
}
}
I access(R x)
{
for(int y=0;x;x=f[y=x])
{
splay(x);
if(c[x][1])
{
val[x].data[0][0]+=max(prd[c[x][1]].data[0][0],prd[c[x][1]].data[1][0]); //因为y变成了实儿子,那么我们就要加上原来实儿子对于g(val)的贡献,减去y对g(val)的贡献
val[x].data[1][0]+=prd[c[x][1]].data[0][0];
}
if(y)
{
val[x].data[0][0]-=max(prd[y].data[0][0],prd[y].data[1][0]);
val[x].data[1][0]-=prd[y].data[0][0];
}
val[x].data[0][1]=val[x].data[0][0];
rc=y;
pushup(x);
}
}
I dfs(R x,R fa)
{
dp[x][1]=a[x]; //用最开始的dp值来初始化f(pre)和g(val)
for(int i=head[x];i;i=node[i].next)
{
int d=node[i].t;
if(d==fa) continue;
dfs(d,x);
f[d]=x;
dp[x][0]+=max(dp[d][0],dp[d][1]);
dp[x][1]+=dp[d][0];
}
val[x].data[0][0]=val[x].data[0][1]=dp[x][0];
val[x].data[1][0]=dp[x][1];
prd[x]=val[x];
}
I modify(R x,R y)
{
access(x); splay(x);
val[x].data[1][0]-=a[x]-y;
pushup(x);
a[x]=y;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
tot=0;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=n-1;++i)
{
int x,y;
scanf("%d %d",&x,&y);
add(x,y); add(y,x);
}
dfs(1,0);
for(int i=1;i<=m;++i)
{
int x,y;
scanf("%d %d",&x,&y);
modify(x,y);
splay(1); //询问前要将1旋转到根,维护修改后的信息
printf("%d\n",max(prd[1].data[0][0],prd[1].data[1][0]));
}
return 0;
}

