题解 P2891 【[USACO07OPEN]吃饭Dining】
安利一波自己的博客
这道题有三倍经验:P1402 酒店之王,P1231 教辅的组成
这道题是一道非常经典的最大流问题,并且限制了每个点只能走一次
思路
首先我们将超级源点连向每一种食物,边权为 \(1\) ,因为每一种食物只能用一次。接下来,我们在将食物和每头喜欢吃这种食物的牛连边,边权同样为 \(1\) ,接下来就是重点,我们将第 \(i\) 个点和第 \(i+n\) 个点连边,边权为 \(1\) ,这样做是为了保证每头牛只能选择一次食物和饮料,至于为什么是对的呢,我们放一张图来理解。
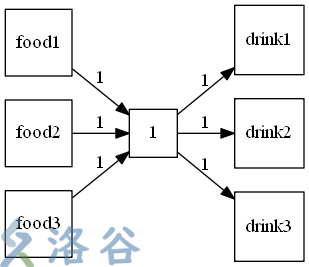
如上图,我们根据题目的要求来说,就是 \(1\) 喜欢吃 食物 \(1\) ,食物 \(2\) 和 食物 \(3\) ,喜欢喝 饮料 \(1\),饮料 \(2\) ,和 饮料 \(3\)。但是如果我们就这么跑的话,答案会是 \(3\) 。显而易见,这是不对的,因为我们这张图没有限制 \(1\) 只能被连接一次,但如果如下图一样建图
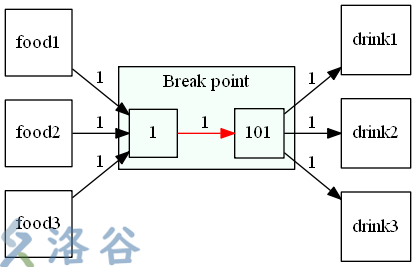
这里我将 \(n\) 固定为 \(100\),因为\(1\leq n,f,d \leq 100\)
如果取的是题目中的 \(n\) ,你就会发现蜜汁 \(WA\) 了 \(5\) 个点
为什么这样子做是对的呢,关键就在于点 \(1\) 和 \(101\) 之间的连边,因为这条边的容量为 \(1\) ,所以不管前面有多大的流,你过去之后都只能变成了 \(1\),从而保证了每个点只经过一次。
接着,将 \(i+n\) 和 \(i\) 喜欢的每一个饮料连边,边权为 \(1\) ,最后,将这些饮料跟超级汇点连边,边权为 \(1\) (注意,最开始的超级源点也要跟每一样食物连一条边权为 \(1\) 的边),这张图就建完了。最后,我们只需要在这张图上跑一下最大流,然后输出这张图的最大流就可以得到答案了。
下面给出这道题样例的图(注意:我没在图上标出反向边):
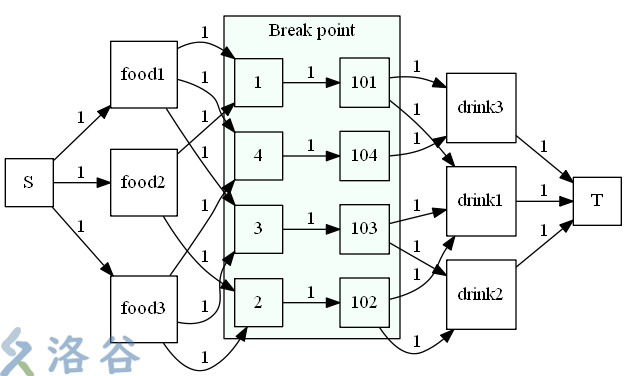
这张图就将就着看一下,虽然我也觉得特别难看
\(Code:\)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define inf 1<<30
#define N 100
using namespace std;
struct Node
{
int t;//t代表通向的点
int next;
int val;//权值
}node[1000011<<1];
int dep[50011],inque[50011];
int head[50011],tot=1;
int maxflow;
int n,p,q;
int s=0,t;
void add(int x,int y,int z)//邻接表存边
{
node[++tot].t=y;
node[tot].next=head[x];
node[tot].val=z;
head[x]=tot;
return;
}
bool bfs()
{
memset(dep,0x3f,sizeof(dep));
memset(inque,0,sizeof(inque));
queue<int>q;
dep[s]=0;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
inque[u]=0;
for(int i=head[u];i;i=node[i].next)
{
int d=node[i].t;
if(node[i].val && dep[d]>dep[u]+1)
{
dep[d]=dep[u]+1;
if(!inque[d])
{
inque[d]=1;
q.push(d);
}
}
}
}
return dep[t]!=0x3f3f3f3f;
}
int dfs(int u,int flow)
{
if(u==t)
{
maxflow+=flow;
return flow;
}
int rlow=0,used=0;
for(int i=head[u];i;i=node[i].next)
{
int d=node[i].t;
if(node[i].val && dep[d]==dep[u]+1)
{
if(rlow=dfs(d,min(flow-used,node[i].val)))
{
used+=rlow;
node[i].val-=rlow;
node[i^1].val+=rlow;
if(used==flow) break;
}
}
}
return used;
}
int Dinic()//我用的是Dinic求最大流,上面均属于最大流部分,可以直接套模板
{
while(bfs())
dfs(s,inf);
return maxflow;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
scanf("%d %d %d",&n,&p,&q);
t=4*N+1;
for(int i=1;i<=p;++i) add(s,i+N,1),add(i+N,s,0); //食物和源点的连边
for(int i=1;i<=q;++i) add(i+3*N,t,1),add(t,i+3*N,0);//饮料和汇点的连边
for(int i=1;i<=n;++i)
{
int fi,di,check;
scanf("%d %d",&fi,&di);
for(int j=1;j<=fi;++j)
{
scanf("%d",&check);
add(check+N,i,1); //check+N表示的就是i喜欢的食物
add(i,check+N,0);
}
add(i,i+2*N,1); //i与i+N的连边,只不过这里将i+N改为i+2*N
add(i+2*N,i,0);
for(int j=1;j<=di;++j)
{
scanf("%d",&check);
add(i+2*N,check+3*N,1); //i+n与饮料的连边
add(check+3*N,i+2*N,0);
}
}
printf("%d",Dinic());//输出最大流
return 0;
}
所以说,网络流的建图还是很关键的


