20162328蔡文琛 week10 大二

20162328 2017-2018-1 《程序设计与数据结构》第十周学习总结

教材学习内容总结

理解图与有向图、无向图
理解带权图
会应用带权图
理解图的广度优先遍历和深度优先遍历
掌握最小生成树算法
掌握图的实现

有向图，无向图

如果给图的每条边规定一个方向，那么得到的图称为有向图，其边也称为有向边。在有向图中，与一个节点相关联的边有出边和入边之分，而与一个有向边关联的两个点也有始点和终点之分。相反，边没有方向的图称为无向图。

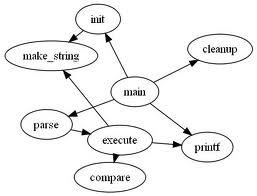
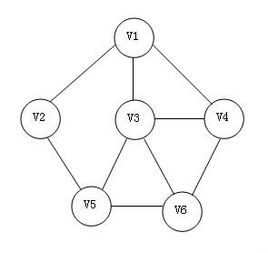
带权图

在处理有关图的实际问题时，往往有值的存在，比如公里数，运费，城市，人口数以及电话部数等。一般这个值成为权值，带权值的图称为带权图或赋权图。也称为网。

最小生成树算法

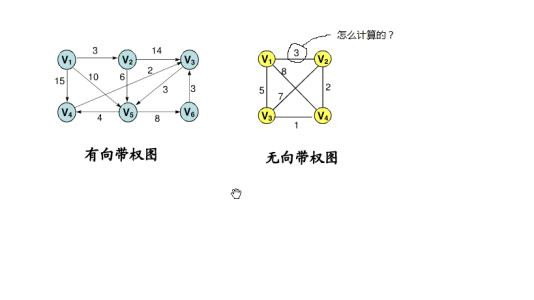
public class WeightedGraph {
    private final int MAX_VERTS = 20; //最大顶点数
    private final int INFINITY = 100000; //最远距离...表示无法达到
    private Vertex[] vertexArray; //存储顶点的数组
    private int adjMat[][]; //存储顶点之间的边界
    private int nVerts; //顶点数量
    private int currentVert; //当前顶点索引
    private PriorityQ thePQ; //存储边的优先级队列
    private int nTree; //最小生成树中的顶点数量

    public WeightedGraph() {
        vertexArray = new Vertex[MAX_VERTS];
        adjMat = new int[MAX_VERTS][MAX_VERTS];
        for(int i = 0; i < MAX_VERTS; i++) {
            for(int j = 0; j < MAX_VERTS; j++) {
                adjMat[i][j] = INFINITY; //初始化所有边界无穷远
            }
        }
        thePQ = new PriorityQ();
    }

    public void addVertex(char lab) { //添加顶点
        vertexArray[nVerts++] = new Vertex(lab);
    }

    public void addEdge(int start, int end, int weight) {//添加带权边
        adjMat[start][end] = weight;
        adjMat[end][start] = weight;
    }

    public void displayVertex(int v) {
        System.out.print(vertexArray[v].label);
    }

    /*
     * 带权图的最小生成树,要选择一条最优的路径
     */
    public void MinSpanningTree() {
        currentVert = 0; //从0开始
        while(nTree < nVerts-1) { //当不是所有节点都在最小生成树中时
            //isInTree是上一节Vertex类中新添加的成员变量 private boolean isInTree;
               //表示有没有加入到树中，初始化为false
vertexArray[currentVert].isInTree = true; //将当前顶点加到树中
            nTree++;

            //往PQ中插入与当前顶点相邻的一些边界
            for(int i = 0; i < nVerts; i++) {
                if(i == currentVert) //如果是本顶点，跳出
                    continue;
                if(vertexArray[i].isInTree) //如果顶点i已经在树中，跳出
                    continue;
                int distance = adjMat[currentVert][i]; //计算当前顶点到i顶点的距离
                if(distance == INFINITY) 
                    continue; //如果当前顶点与i顶点无穷远，跳出
                putInPQ(i, distance); //将i节点加入PQ中
            }

            if(thePQ.size() == 0) { //如果PQ为空，表示图不连接
                System.out.println("Graph not connected!");
                return;
            }

            Edge theEdge = thePQ.removeMin();
            int sourceVert = theEdge.srcVert;
            currentVert = theEdge.destVert;

            System.out.print(vertexArray[sourceVert].label);//这里就是一步步打印最小生成树的路径
            System.out.print(vertexArray[currentVert].label);
            System.out.print(" ");
        }
    }
    //这个方法是将一个Edge放入优先级队列，保证队列中每个Edge的des顶点是不同的。
    private void putInPQ(int newVert, int newDist) {
        int queueIndex = thePQ.find(newVert);//判断PQ中是否已经有到相同目的顶点的边界
        if(queueIndex != -1) { //如果有则与当前顶点到目的顶点的距离作比较，保留短的那个
            Edge tempEdge = thePQ.peekN(queueIndex);//get edge
            int oldDist = tempEdge.distance;
            if(oldDist > newDist) { //如果新的边界更短
                thePQ.removeN(queueIndex); //删除旧边界
                Edge theEdge = new Edge(currentVert, newVert, newDist);
                thePQ.insert(theEdge);
            }
        }
        else { //如果PQ中没有到相同目的顶点的边界
            Edge theEdge = new Edge(currentVert, newVert, newDist);
            thePQ.insert(theEdge);//直接添加到PQ
        }
    }
}