解题报告 概率与期望 2025/03/07 ~ ? (未完工)
解题报告 概率与期望 2025/03/07 ~ 2025/??/??
A. 给定一个带边权的 DAG。对于一个出度为 \(k\) 的节点,有 \(\frac{1}{k}\) 的概率走向每一条边。求从 \(1\) 到 \(n\) 的边权和的期望。
定义状态 \(dp_i\) 代表从 \(i\) 到 \(n\) 边权和的期望,显然有 \(dp_n=0\)。
考虑转移,记 \(edge_u\) 表示 \(u\) 的出边的集合,\(out_u\) 表示 \(u\) 的出度,那么对于点 \(u\) 有
也就是说,我们可以通过逆推,从 \(n\) 向 \(1\) 转移。
实现上,反向建图,进行一次拓扑排序,顺便进行转移。
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
const int maxn = 100000 + 10;
int n, m;
vector<pair<int, int>> e[maxn];
int in[maxn];
int deg[maxn];
double dp[maxn];
void toposort()
{
queue<int> Q;
Q.push(n);
while (!Q.empty())
{
int u = Q.front();
Q.pop();
for (auto it : e[u])
{
int v = it.first, w = it.second;
dp[v] += (dp[u] + w) / deg[v];
if (--in[v] == 0)
Q.push(v);
}
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int u, v, w;
cin >> u >> v >> w;
e[v].push_back(make_pair(u, w));
in[u]++, deg[u]++;
}
toposort();
cout << fixed << setprecision(2) << dp[1] << endl;
return 0;
}
B. 给定一个
01串。每个字符有 \(p_i\) 的概率为1,否则为0。对于这个串中极长一串1,若其长度为 \(x\),则其贡献为 \(x^3\)。求整个串贡献的期望。
三次方期望显然没法做。
考虑已有长度为 \(x\) 的一串 1,如果再增加一个 1,显然贡献由 \(x^3\) 变为 \((x+1)^3\)。
易得增加的贡献为 \(3\times x^2+3\times x+1\)。
然后我们就可以按这个式子拆开考虑。
\(x\) 的期望明显是好做的,记其为 \(x1\),那么有 \(x1_i=(x1_{i-1}+1)\times p_i\)。
这时 \(x^2\) 的期望就可做了,记其为 \(x2\),则 \(x2_i=(x2_{i-1}+2\times x2_{i-1}+1)\times p_i\)。
于是我们就有了 \(x^3\) 的期望:\(x3_i=(x3_{i-1}+3\times x2_{i-1}+3\times x1_{i-1}+1)\times p_i\)。
值得注意的是 \(x3_n\) 并非是要求的答案,因为我们的递推只考虑了当前这一位,而要求的是最终分数即前 \(n\) 位。
于是我们对 \(x^3\) 的递推式变形:\(x3_i=(x3_{i-1}+3\times x2_{i-1}+3\times x1_{i-1}+1)\times p_i+x3_{i-1}\times(1-p_i)=x3_{i-1}+(3\times x2_{i-1}+3\times x1_{i-1}+1)\times p_i\),此时求得的 \(x3_n\) 才是正确答案。
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
const int maxn = 100000 + 10;
int n;
double p[maxn];
double x1[maxn], x2[maxn];
double ans[maxn];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
cin >> p[i];
for (int i = 1; i <= n; i++)
{
x1[i] = (x1[i - 1] + 1) * p[i];
x2[i] = (x2[i - 1] + 2 * x1[i - 1] + 1) * p[i];
ans[i] = ans[i - 1] + (3 * (x1[i - 1] + x2[i - 1]) + 1) * p[i];
}
cout << fixed << setprecision(1) << ans[n] << endl;
return 0;
}
C. 一套试卷有 \(n\) 道单选题,第 \(i\) 题有 \(a_i\) 个选项。作答时第 \(i\) 题的答案写串到了第 \(i+1\) 题上,第 \(n\) 题的答案写串到了第 \(1\) 题上。求做对题目总数的期望。
诈骗题。
根据期望的线性性,做对题目总数的期望等于每一题做对概率的和。
显然第 \(i\) 题能否答对只跟第 \(i-1\) 题有关,记 \(p_i\) 为第 \(i\) 题做对的概率,即第 \(i-1\) 题和第 \(i\) 题答案相同的概率。
若 \(a_{i-1}\le a_i\),\(p_i=\dfrac{1}{a_i}\),否则 \(p_i=\dfrac{1}{a_{i-1}}\)。
扫一遍即可。
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
const int maxn = 10000000 + 10;
int n, A, B, C;
int a[maxn];
double ans;
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> A >> B >> C >> a[1];
for (int i = 2; i <= n; i++)
a[i] = (a[i - 1] * A + B) % 100000001;
for (int i = 1; i <= n; i++)
a[i] = a[i] % C + 1; // 题目要求的奇异搞笑读入方式
a[n + 1] = a[1];
for (int i = 2; i <= n + 1; i++)
ans += 1.0 / max(a[i - 1], a[i]);
cout << fixed << setprecision(3) << ans << endl;
return 0;
}
D. 有 \(R\) 张红牌和 \(B\) 张黑牌,洗牌后进行翻牌。翻到一张红牌赢 \(1\) 元,一张黑牌输 \(1\) 元。可以随时停止翻牌。求期望最多能赢多少钱。
记 \(dp_{i,j}\) 为剩 \(i\) 张红牌 \(j\) 张黑牌时的最大收益。
显然有 \(dp_{i,0}=i,dp_{0,j}=0\)。
转移即为 \(dp_{i,j}=\max(0,(dp_{i-1,j}+1)\times \dfrac{i}{i+j}+(dp_{i,j-1}-1)\times \dfrac{j}{i+j})\)。
对 \(0\) 取 \(\max\) 即是说这时到最后的期望收益为负,不用再翻了。
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
const int maxn = 5000 + 10;
int r, b;
double dp[maxn][maxn];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> r >> b;
for (int i = 1; i <= r;i++)
dp[i][0] = (double)i;
for (int i = 1; i <= r; i++)
for (int j = 1; j <= b;j++)
dp[i][j] = max(0.0, (dp[i - 1][j] + 1.0) * i / (i + j) + (dp[i][j - 1] - 1.0) * j / (i + j));
cout << fixed << setprecision(6) << dp[r][b] - 0.0000005 << endl;
return 0;
}
E. 给定正整数数列 \(h_1,h_2,\cdots,h_n\)。设 \(p\) 为 \(1\sim n\) 的随机排列。定义 \(h'_i=h_{p_i}\)。定义 \(\mathrm{pre}_i\) 为最大的 \(j\lt i\) 满足 \(h'_j\ge h'_i\)(如果不存在,规定为 \(0\))。求出 \(\displaystyle \sum_{i=1}^n (i-\mathrm{pre}_i)\) 的期望值,保留两位小数输出。
建议去看原题面。这里提供的是洛谷的形式化题意。接下来的讲解会使用原题面的表述。
所有人视野距离和的期望等于每个人期望视野距离的和。于是我们考虑对于每个人单独计算期望。
对于第 \(i\) 个人,一定只有身高小于 \(h_i\) 的人能对其产生贡献。设有 \(s\) 个这样的人。易得每个人能产生的贡献均为 \(1\)。
我们从 \(s\) 中随便选一个人 \(j\) 进行计算。
\(j\) 对 \(i\) 有贡献,当且仅当 \(j\) 在剩余的 \(n-s\) 人中正好在 \(i\) 的前面一个位置。否则这 \(n-s\) 个人的身高一定大于等于 \(h_i\),\(i\) 看不到 \(j\)。应用插板法,一共有 \(n-s+1\) 个空位,显然 \(j\) 对 \(i\) 有贡献的概率为 \(\dfrac{1}{n-s+1}\)。由于这样的人有 \(s\) 个,再设身高为 \(h_i\) 的人有 \(t\) 个,那么总的概率就是 \(\dfrac{s\times t}{n-s+1}\),既然贡献为 \(1\),期望也是这个值。
此外每人无论如何都有 \(1\) 的贡献。
实现上,记录 \(t\) 后从小到大遍历 \(h\),并动态统计 \(s\)。
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
const int maxn = 300 + 10;
const int maxv = 1000 + 10;
int n, h[maxn];
int maxh, cnt[maxv];
int s;
double ans;
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> h[i];
cnt[h[i]]++;
maxh = max(maxh, h[i]);
}
for (int i = 1; i <= maxh; i++)
{
ans += 1.0 * s * cnt[i] / (n - s + 1) + cnt[i];
s += cnt[i];
}
cout << fixed << setprecision(2) << ans << endl;
return 0;
}
F. 对于一个 \(n\times m\) 的矩阵,进行 \(k\) 次操作,每次随机选择 \((x_1,y_1), (x_2,y_2)\) 并将以这两个格子为对角的矩形上色。求最后被上色格子个数的期望。
仍然是贡献为 \(1\),期望 = 概率。
发现一个格子会被反复上色,被上色的概率不好算,我们考虑它不被上色的概率。
每次操作时对于一个格子 \((i,j)\),它不被上色当且仅当选定的两个点都在上面/下面/左面/右面。
根据容斥原理发现四角会重复计算贡献,需要减掉一次。
记这个概率为 \(p\),那么这个格子在所有 \(k\) 次操作中至少被染色一次的概率就是 \(1-p^k\)。
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
int k, n, m;
double ans;
double sq(double x) { return x * x; }
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> k >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
double painted;
painted = sq((i - 1) * m) + sq((n - i) * m) + sq((j - 1) * n) + sq((m - j) * n);
painted -= sq((i - 1) * (j - 1)) + sq((i - 1) * (m - j)) + sq((n - i) * (j - 1)) + sq((n - i) * (m - j));
ans += 1 - pow(painted / sq(n * m), k);
}
cout << fixed << setprecision(0) << ans << endl;
return 0;
}
G. 对于一个给定的仅由
x,o,?组成的字符串,对于每段极长的o,其长度为 \(a\),就有 \(a^2\) 的贡献。?表示这一位上x和o各有 \(50\%\) 的可能性。求期望的总贡献。
记录一个数 \(combo\) 表示当前连续 o 的期望长度,\(dp_i\) 表示前 \(i\) 位的期望贡献。
显然 \(dp_i\) 的转移按字符种类讨论。
-
当前字符为
o时,\(dp_i=dp_{i-1}+2\times combo+1\)。 -
当前字符为
x时,\(dp_i=dp_{i-1}\)。 -
当前字符为
?时,将上述两种转移合起来,然后乘上概率 \(\dfrac{1}{2}\) 就好了。
\(combo\) 的转移显然。
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
const int maxn = 300000 + 10;
int n;
string s;
long double combo, dp[maxn];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> s;
for (int i = 1; i <= n; i++)
{
char op = s[i - 1];
if (op == 'x')
{
dp[i] = dp[i - 1];
combo = 0;
}
else if (op == 'o')
{
dp[i] = dp[i - 1] + 2 * combo + 1;
combo++;
}
else
{
dp[i] = dp[i - 1] + combo + 0.5;
combo = (combo + 1) / 2;
}
}
cout << fixed << setprecision(4) << dp[n] << endl;
return 0;
}
J. NOIP2016 换教室。简要题意不会写。
考虑 Floyd 求出图上任意两点最短路。
设计状态 \(dp_{i,j,k}\) 表示当前时间为 \(i\),申请换了 \(j\) 次教室,上一次是否申请 \((k\in \{0,1\})\) 的期望体力消耗。
状态转移可以按如下的表格来分类讨论。
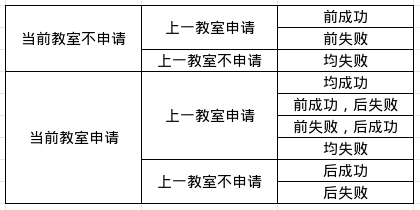
然后状态转移方程很容易得到。
dp[i][j][0] = min(dp[i - 1][j][1] + p[i - 1] * g[d[i - 1]][c[i]] + (1 - p[i - 1]) * g[c[i - 1]][c[i]], // 前一个申请
dp[i - 1][j][0] + g[c[i - 1]][c[i]]); // 前一个不申请
dp[i][j][1] = min(dp[i - 1][j - 1][1] + p[i - 1] * p[i] * g[d[i - 1]][d[i]] + p[i - 1] * (1 - p[i]) * g[d[i - 1]][c[i]] + (1 - p[i - 1]) * p[i] * g[c[i - 1]][d[i]] + (1 - p[i - 1]) * (1 - p[i]) * g[c[i - 1]][c[i]], // 前一个申请
dp[i - 1][j - 1][0] + p[i] * g[c[i - 1]][d[i]] + (1 - p[i]) * g[c[i - 1]][c[i]]); // 前一个不申请
虽然长但是很符合直觉。
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long long
const int inf = 0x3f3f3f3f;
const int maxn = 2000 + 10;
const int maxv = 300 + 10;
int n, m, ver, edge;
int g[maxn][maxn];
int c[maxn], d[maxn];
double p[maxn];
double dp[maxn][maxn][2];
void Floyd()
{
for (int k = 1; k <= ver; k++)
for (int i = 1; i <= ver; i++)
for (int j = 1; j <= ver; j++)
g[i][j] = g[j][i] = min(g[i][j], g[i][k] + g[k][j]);
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m >> ver >> edge;
for (int i = 1; i <= n; i++)
cin >> c[i];
for (int i = 1; i <= n; i++)
cin >> d[i];
for (int i = 1; i <= n; i++)
cin >> p[i];
for (int i = 1; i <= ver; i++)
for (int j = 1; j <= ver; j++)
g[i][j] = g[j][i] = inf;
for (int i = 1; i <= ver; i++)
g[i][i] = 0;
for (int i = 1; i <= edge; i++)
{
int u, v, w;
cin >> u >> v >> w;
g[u][v] = g[v][u] = min(g[u][v], w);
}
Floyd();
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
dp[i][j][0] = dp[i][j][1] = inf;
dp[1][0][0] = dp[1][1][1] = 0;
for (int i = 2; i <= n; i++)
for (int j = 0; j <= m; j++)
{
// 当前不申请
dp[i][j][0] = min(dp[i - 1][j][1] + p[i - 1] * g[d[i - 1]][c[i]] + (1 - p[i - 1]) * g[c[i - 1]][c[i]], // 前一个申请
dp[i - 1][j][0] + g[c[i - 1]][c[i]]); // 前一个不申请
// 当前申请
if (j != 0)
dp[i][j][1] = min(dp[i - 1][j - 1][1] + p[i - 1] * p[i] * g[d[i - 1]][d[i]] + p[i - 1] * (1 - p[i]) * g[d[i - 1]][c[i]] + (1 - p[i - 1]) * p[i] * g[c[i - 1]][d[i]] + (1 - p[i - 1]) * (1 - p[i]) * g[c[i - 1]][c[i]], // 前一个申请
dp[i - 1][j - 1][0] + p[i] * g[c[i - 1]][d[i]] + (1 - p[i]) * g[c[i - 1]][c[i]]); // 前一个不申请
}
double ans = inf;
for (int i = 0; i <= m; i++)
for (int j = 0; j <= 1; j++)
ans = min(ans, dp[n][i][j]);
cout << fixed << setprecision(2) << ans << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号