【算法笔记】二维凸包
- 本文总计约 11000 字,阅读大约需要 40 分钟。
前言
二维凸包是计算几何中最经典的算法了,从这里可以引出很多计算几何的其它算法。
事实上,二维凸包的算法并不难,甚至比提高组的 Tarjan 算法还要直观一些(毕竟笔者学习 Tarjan 用了好长时间,但学习二维凸包只用了三天 QwQ),但是代码非常麻烦,需要读者努力去理解。
本篇凸包详细地介绍了三种求凸包的算法,并使用 Geogebra 画图,希望能够为读者带来良好的阅读体验。
说句题外话,洛谷上凸包的模板题居然不卡 Jarvis,我本来是想看看自己 Jarvis 写没写挂的,结果一发就 AC 了,还挺惊喜的 QwQ
问题引入
一个偶然的机会下,小 \(P\) 来到了一块广阔无垠的土地上。他位于这块土地的正中心处,以北为 \(y\) 轴正方向,东为 \(x\) 轴正方向,整块土地看成一个平面直角坐标系。
这块土地下资源丰富,小 \(P\) 实地考察后发现这里有 \(n\) 个地方埋有大量的矿藏供他开采,这 \(n\) 个采矿点的位置可以用坐标表示为 \((x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)\)。
小 \(P\) 决定在这里用围墙把这 \(n\) 个采矿点全部围起来,开办一个巨大的矿场,作为他的收入来源。但是修筑围墙也是需要成本的,所以他想知道,将这些采矿点全部用围墙围起来,围墙的长度 \(L\) 至少应该为多少呢?注意,小 \(P\) 规定,如果一个采矿点刚好在围墙下面,就认为是在矿场内部。
样例输入:\(n=9\),采矿点坐标为 \((1,1),(0,3),(3,0),(3,2),(2,4),(5,4),(5,1),(7,2),(4,3)\)。
样例输出:\(L=5\sqrt{5}+2\sqrt{2}+3\),采矿场的形状如下图:
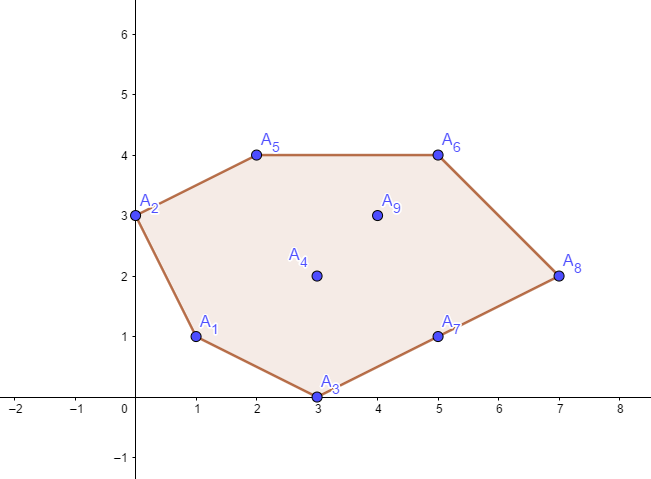
前置知识
凸包的概念
像上面的题目一样,在平面中有若干个点,画一个凸多边形,将这些点完全覆盖。那么使这个凸多边形最小的凸多边形,称为凸包。
更具体地想象一下:你面前有一个钉满钉子的桌子,假如用一根橡皮圈,将这些钉子完全包围在里面的橡皮圈,就是这些钉子的凸包。
向量的叉乘
如果你不知道什么是向量,请回去重修高中数学必修二 OvO。
对于空间中的两个向量,我们称叉乘的结果为叉积,两个向量的叉积依旧为一个向量。
两个向量的叉积的模长为两向量的模长的乘积再乘以两向量的夹角,即 \(\left| \vec{a} \times \vec{b} \right|=|\vec{a}|\cdot |\vec{b}|\cdot \sin\left\langle{\vec{a},\vec{b}}\right\rangle\);方向满足右手定则:使右手食指指向 \(\vec{a}\) 的方向,中指指向 \(\vec{b}\) 的方向,此时,大拇指指向的方向即为 \(\left(\vec{a}\times\vec{b}\right)\) 的方向。
并且,下面给出两个向量的叉积计算公式:若 \(\vec{a}=(x_1,y_1,z_1),\vec{b}=(x_2,y_2,z_2)\),那么我们有:
显然向量的叉乘不满足交换律,但是满足反交换律,即:\(\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}\)。
向量叉积可以认为是从一个向量旋转到另一个向量的过程,所以我们可以用 \(\vec{a}\) 和 \(\vec{b}\) 的叉积的符号来判断从 \(\vec{a}\) 的方向旋转到 \(\vec{b}\) 的方向是顺时针旋转还是逆时针旋转,在凸包算法中会被广泛使用。
在下文,为了方便表述,在不引起歧义的情况下,我们使用一对有序点对 \(\left\langle A,B \right\rangle\) 代表向量 \(\stackrel{\longrightarrow}{AB}\)。
极坐标和极角
在平面中,选取某一定点点 \(O\) 做射线 \(Ox\),我们就构成了一个平面极坐标系,对于平面内任意一点 \(M\),连接 \(OM\),那么我们定义 \(\rho=|OM|\),\(\stackrel{\longrightarrow}{OM}\) 与 \(\stackrel{\longrightarrow}{Ox}\) 的夹角为 \(\theta\),那么 \(M\) 就可以由一对有序数对 \((\rho,\theta)\) 唯一确定,其中 \(\rho\ge 0,\theta\in[0,2\pi)\)。这个数对就被称为点 \(M\) 的极坐标,\(\rho\) 称为 \(M\) 的极径,\(\theta\) 称为 \(M\) 的极角。
凸包暴力算法 — — Jarvis 算法
内容
按照惯例,我们会先想想:暴力怎么做?
首先易证,一个点集的凸包是一定存在的。那么问题在于如何构造凸包。于是,这里就要隆重介绍一种算法:Jarvis 步进法,又称卷包裹法。
卷包裹法,顾名思义,就像是用一张纸,将这些点集慢慢地像卷地毯一样包起来。它的步骤大致如下:
- 选取其中一个点,一般选择 \(x\) 坐标最小的情况下,\(y\) 坐标最小的点,因为我们能保证这个点显然在凸包的顶点上;
- 从当前节点向所有节点连线,选择一条线段,使得所有的点都在这条线段的左侧,且线段长度最长,那么这条线段是凸包的一条边;
- 以这条线段的另一个端点为轴,重复操作 2,直到凸包完全封闭起来。
例如,这样的一个点集,我们如何求它的凸包呢?

第一步,我们要选择这里面最靠左的一个点,并向其他点连线段,如图:
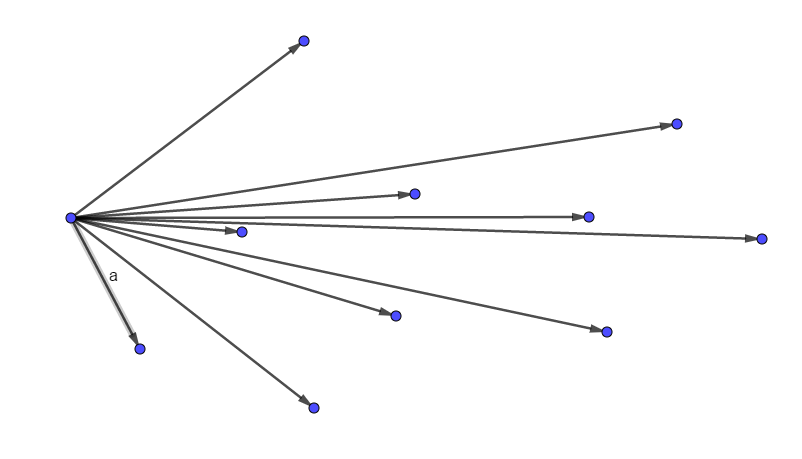
我们发现,其中标为 \(a\) 的线段可以保证所有的点都在其左侧,所以它是凸包的一条边。
接下来,选择 \(a\) 的另一个端点,向其它的点连线段,找到标为 \(b\) 的线段,也是凸包的一个端点。
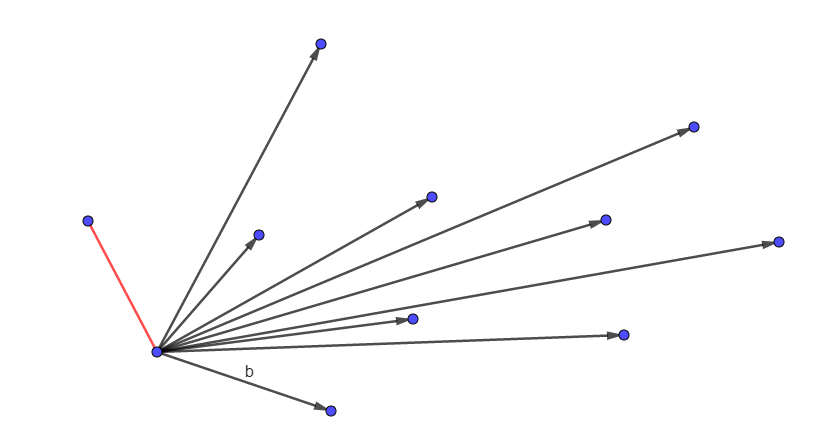
于是,我们就可以愉快地卷起来辣 QwQ,最后不断重复上述步骤,卷过一周后,就可以找到它的凸包是这样的:
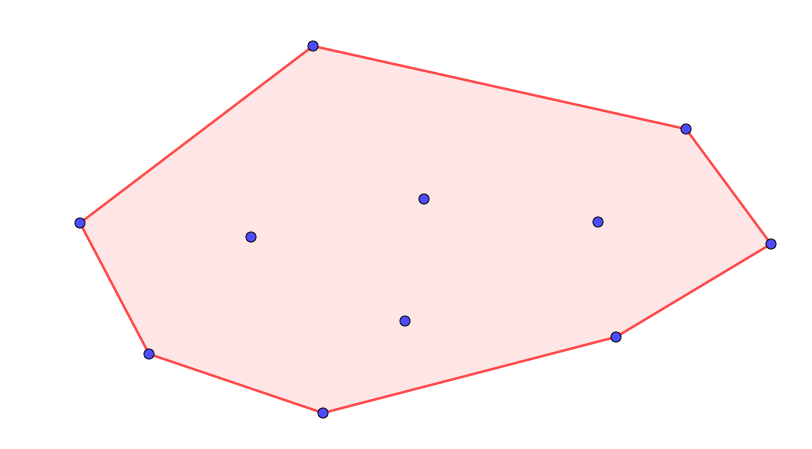
如何判断哪个向量在左边呢?很简单,用上面所说的向量叉乘的方法就可以了:考虑下面的两个向量 \(\vec{u}=(x_1,y_1,0),\vec{v}=(x_2,y_2,0)\)。
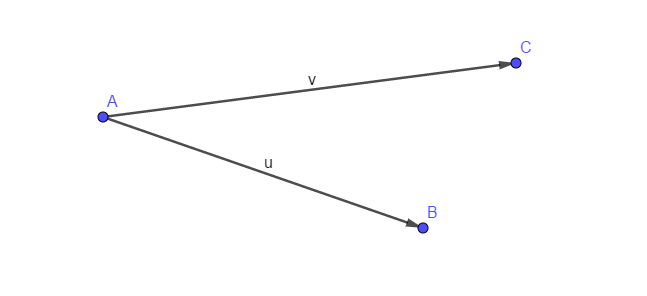
通过计算,我们可以发现 \(\vec{u}\times \vec{v}\) 的 \(z\) 坐标为 \(x_1y_2-x_2y_1>0\),这也就是说,\(\vec{u}\) 要想绕到 \(\vec{v}\) 的方向上,需要逆时针旋转,那么 \(\vec{v}\) 就在 \(\vec{u}\) 的左边了。
通过这样的过程,我们就可以求出一个平面点集的二维凸包了。
代码
代码其实不难写,就是有点麻烦:
#include <algorithm> //使用 swap 函数
#include <cstdio>
#include <cmath> //使用 sqrt 函数
using namespace std;
const int maxN = 100001;
int n, cur, nxt;
struct Point {
double x, y;
bool operator < (Point P) { //找到横坐标最小的情况下,纵坐标最小的点
if(x != P.x) {
return x < P.x;
}
else {
return y < P.y;
}
}
} point[maxN];
double tot;
inline double det(Point A, Point B, Point C) { //求出向量 <A,B> 与 <A,C> 的叉积的 z 坐标
double yB = B.y - A.y, yC = C.y - A.y,
xB = B.x - A.x, xC = C.x - A.x;
return xB * yC - xC * yB;
}
inline double dis(Point A, Point B) { //求两点间距离
return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}
int main(void) {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%lf%lf", &(point[i].x), &(point[i].y));
if(point[i] < point[1]) { //始终使 1 号点为起始点
swap(point[i], point[1]);
}
}
cur = 1; //从一号节点开始 “卷包裹”
do {
nxt = 1;
for(int i = 1; i <= n; ++i) {
if(i == nxt || i == cur) {
continue ;
}
if(det(point[cur], point[nxt], point[i]) < 0) { //找到了一个更“右侧”的点
nxt = i;
}
else if(det(point[cur], point[nxt], point[i]) == 0 &&
dis(point[cur], point[i]) > dis(point[cur], point[nxt])) { //或者找到了更远的点
nxt = i; //更新 nxt 点
}
}
tot += dis(point[cur], point[nxt]); //周长增加凸包的对应边长
cur = nxt;
} while(cur != 1);
printf("%.2lf", tot);
return 0;
}
//by CaO
时间复杂度分析
我们设一共有 \(n\) 个点,其中有 \(m\) 个点能成为凸包的顶点,那么对每个顶点,我们都要遍历 \(n\) 个点,一共要进行 \(n\times m\) 次比较操作,时间复杂度为 \(\Theta(nm)\)。
然而,在随机生成的数据下,\(m\) 的值可能会非常小,其时间复杂度接近于 \(\Omega(n)\)。所以 Jarvis 步进法在随机点集下表现优秀,是可以用它来解决凸包问题的。
Graham 算法
暴力的缺陷和 Graham 算法的引入
如同上文所说,Jarvis 确实在随机图下表现优秀。然而,如果我们特殊构造数据,很容易就会构造出 \(n=m\) 或者 \(n\) 与 \(m\) 相差不大的数据,这种情况下,Jarvis 步进法就可以被卡到 \(\mathcal{O}(n^2)\),假如 \(n\le 10^5\),就有可能会 TLE。正如 SPFA 一样,随机图下表现优秀,但是如果数据被特殊构造过,就会被卡爆了。
所以关于 Jarvis,它死了我们需要一种更快的算法,在 \(\mathcal{O}(n\log n)\) 甚至是 \(\mathcal{O}(n)\) 的复杂度内解决这个问题。
Graham 算法概述
Graham 算法是由美国数学家 \(\mathcal{Ronald\ Graham}\) 发现的算法。可以做到 \(\mathcal{O}(n\log n)\) 排序,\(\Theta(n)\) 求解平面点集的二维凸包。这样,就可以将二维凸包算法的时间复杂度降到 \(\mathcal{O}(n\log n)\)。
Graham 算法的步骤
它的步骤如下:
- 与 Jarvis 步进法一样,选取 \(x\) 坐标最小的情况下,\(y\) 坐标最小的点为原点,接下来,按照极角从小到大的顺序对另外 \((n-1)\) 个点排序。
- 顺序枚举所有的点,并使它们依次入栈。在这个过程中,始终使栈内的点序列保持“左转”的顺序,如果出现了即将入栈的点和栈顶的两个点形成了“右转”的图案,那么就让栈顶出栈。
- 直到所有的点都被枚举完后,依次连接栈序列内的点,就形成了这个点集的凸包。
当然,只罗列步骤是很抽象的,我们用上面那张图来模拟一下 Graham 的步骤:
第一步,找到 \(x\) 坐标最小的点 \(A_1\),接下来,按极角从小到大,分别标上 \(A_2,A_3,\cdots\),如图所示。
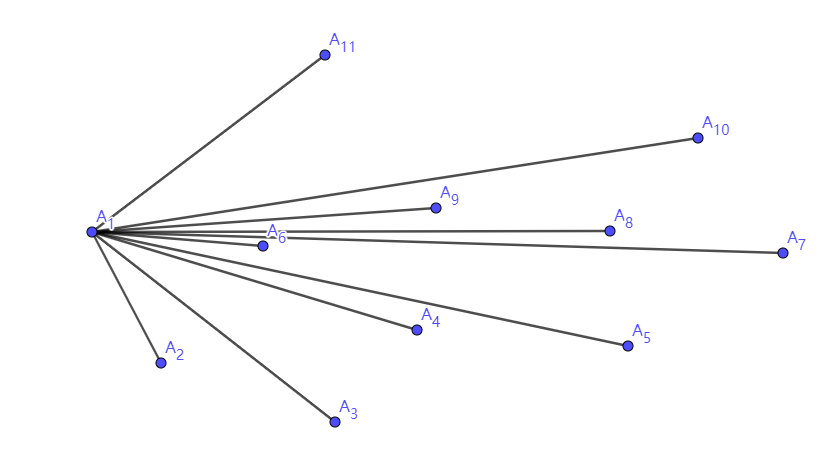
第二步,\(A_1\) 入栈,然后找到极角最小的点 \(A_2\),\(A_2\) 入栈。

第三步,找到 \(A_3\),因为折线 \(A_1-A_2-A_3\) 依旧满足凸包的性质,我们使它入栈。同理,\(A_4\) 也满足凸包的性质,入栈。
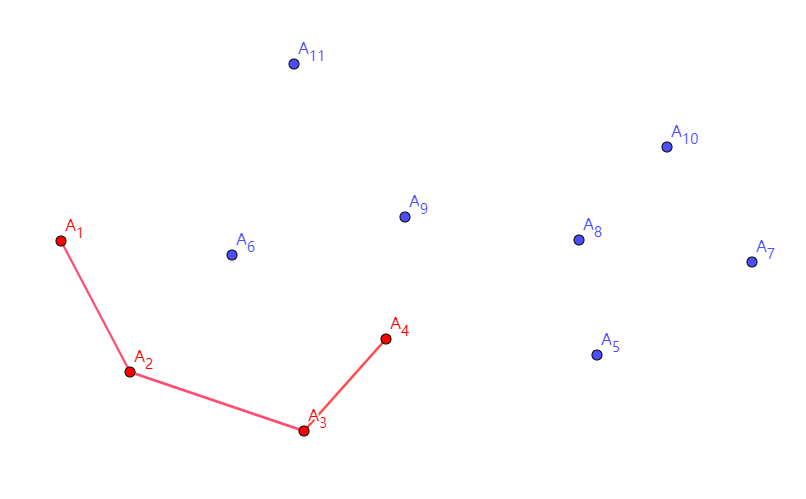
第五步,发生了一些变化,扫描到了点 \(A_5\),它与 \(A_4\) 形成了右拐的局面!这个时候,我们就要把 \(A_4\) 弹出栈,并将 \(A_5\) 入栈。
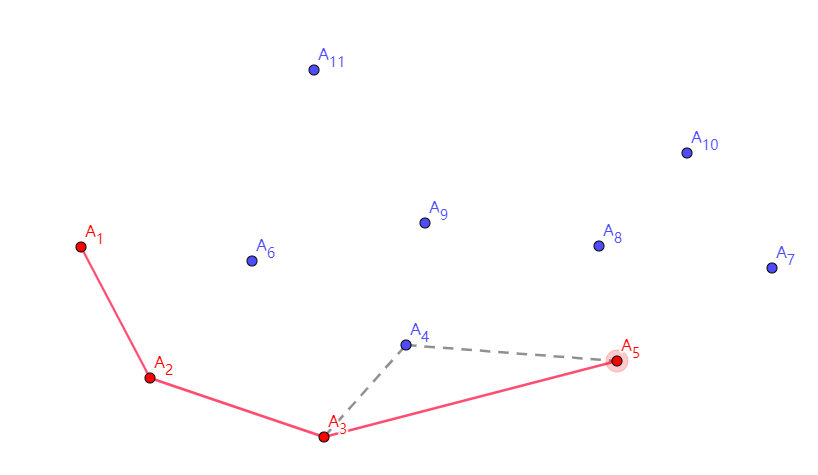
接下来,\(A_6\) 顺利入栈,但是因为 \(A_5-A_6-A_7\) 又形成了右拐的局面,所以 \(A_6\) 出栈,\(A_7\) 入栈。
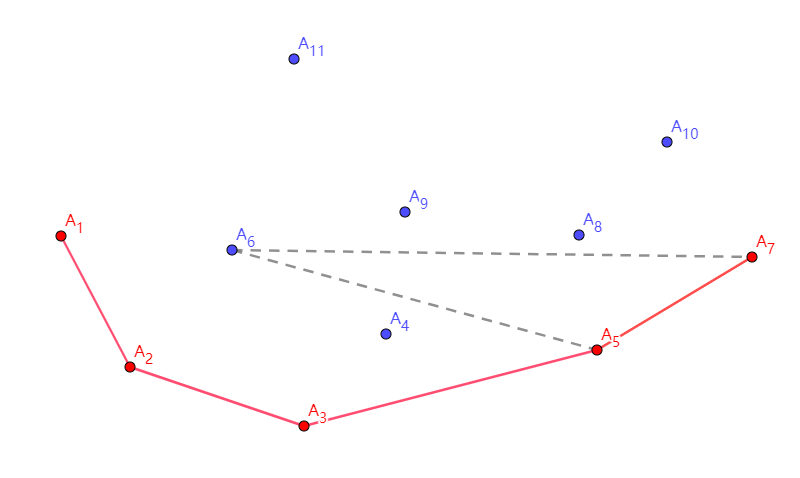
\(A_8,A_9\) 顺利入栈。
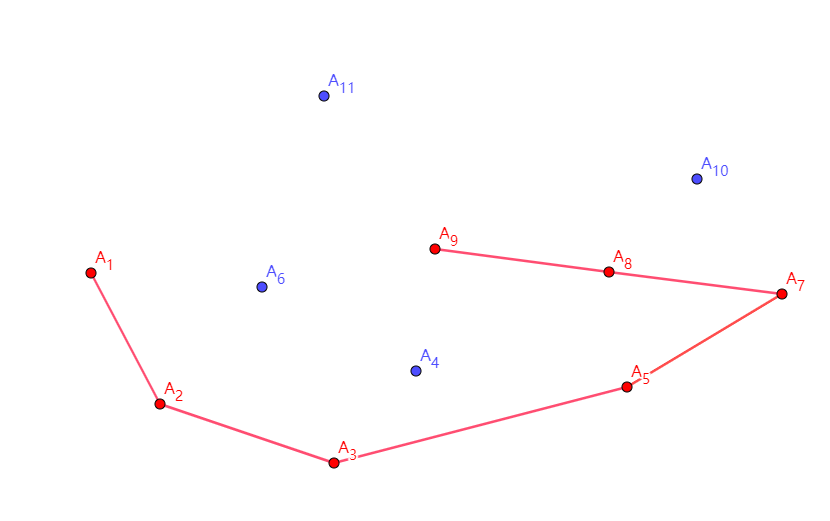
但是接下来出现了 \(A_{10}\)!它首先踢掉了 \(A_9\),
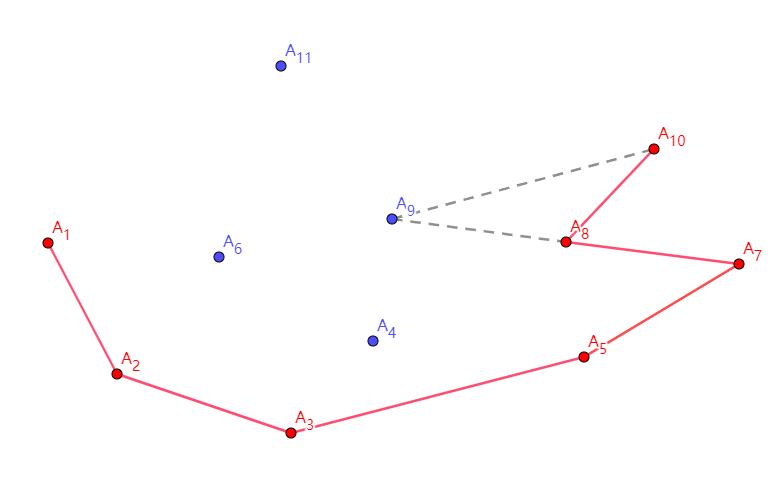
又踢掉了 \(A_8\),这个时候栈内元素又形成凸包了,就可以让 \(A_{10}\) 入栈了。同时 \(A_{11}\) 也可以一马平川地入栈:
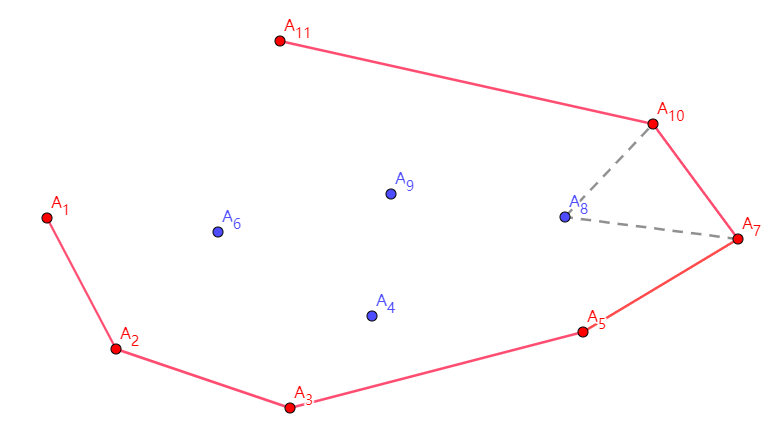
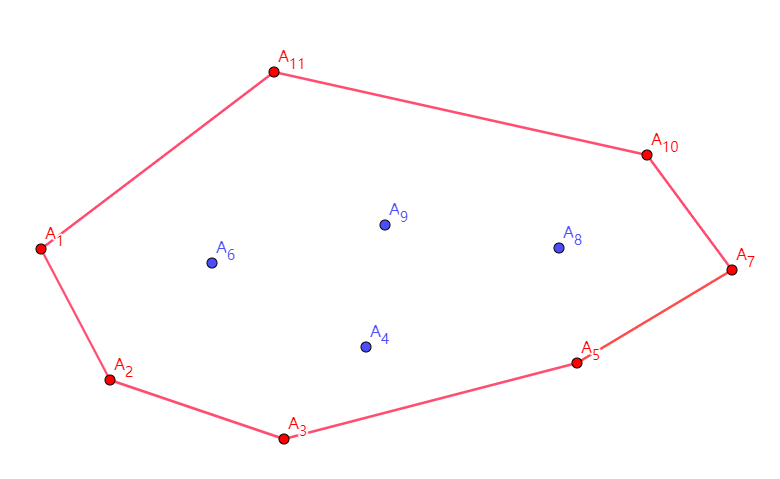
栈内的序列为 \(A_1,A_2,A_3,A_5,A_7,A_{10},A_{11}\),顺次连接,就得到了我们所要求的凸包了。
还有一个小细节:怎么求一个点的极角?这里可以用平面直角坐标系和极坐标系的坐标转换,即 \(x=\rho \cos\theta,y=\rho\sin\theta\),那么极角 \(\theta=\arctan{\dfrac{y}{x}}\),C++ 的 <cmath> 库中提供了 atan() 函数,可以直接拿来用,注意特判 \(x=0\) 的情况就可以了。当然,直接使用 Jarvis 中叉积的方法来为点排序也可以。
代码
#include <algorithm> //使用 swap 函数
#include <cstdio>
#include <cmath> //使用 sqrt 函数
using namespace std;
const int maxN = 100001;
int n, top, stac[maxN]; //手写栈
struct Point {
double x, y;
bool operator < (Point P) { //找到横坐标最小的情况下,纵坐标最小的点
if(x != P.x) {
return x < P.x;
}
else {
return y < P.y;
}
}
} point[maxN];
double tot;
inline double det(Point A1, Point A2, Point B1, Point B2) { //求出向量 <A1,A2> 与 <B1,B2> 的叉积的 z 坐标
return (A2.x - A1.x) * (B2.y - B1.y) - (B2.x - B1.x) * (A2.y - A1.y);
}
inline double dis(Point A, Point B) { //求两点间距离
return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}
inline bool cmp(Point A, Point B) { //sort 的 cmp 函数
double tmp = det(point[1], A, point[1], B);
if(tmp > 0) { //通过叉积判断极角从小到大
return true;
}
else if (tmp == 0 && dis(point[1], A) < dis(point[1], B)) { //距离由近及远
return true;
}
else {
return false;
}
}
int main(void) {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%lf%lf", &(point[i].x), &(point[i].y));
if(point[i] < point[1]) { //始终使 1 号点为起始点
swap(point[i], point[1]);
}
}
sort(point + 2, point + n + 1, cmp);
stac[++top] = 1;
for(int i = 2; i <= n; ++i) {
while(top > 1 && det(point[stac[top - 1]], point[stac[top]], point[stac[top]], point[i]) <= 0) { //找到下凹的点就让它出栈
stac[top--] = 0;
}
stac[++top] = i; //i 点入栈
}
stac[++top] = 1; //使凸包封闭
for(int i = 1; i < top; ++i) {
tot += dis(point[stac[i]], point[stac[i + 1]]); //计算周长
}
printf("%.2lf", tot);
return 0;
}
//by CaO
时间复杂度分析
Graham 算法需要用 \(\mathcal{O}(n \log n)\) 的时间复杂度对点进行排序预处理,然后顺次扫描每个点。因为每个点都要入栈一次,并且最多出栈一次,所以扫描的时间复杂度为 \(\Theta(n)\)(算法正文甚至比预处理还要高效 OvO)。而且我们发现 Graham 算法好像比 Jarvis 步进法码量大不了多少,所以在处理实际问题的时候,也一般是使用 Graham 算法(或下文的 Andrew 算法)。
实际上,这就是单调栈的思想,它在一些 dp 题目的线性优化里也很有用途,是值得我们学习的思想。
Andrew 算法
Andrew 算法概述
尽管 Graham 算法已经非常高效了,但是按照极角排序是性能比较差的,而且是不必要的。我们想:如果能够直接按照 \(x,y\) 坐标排序的话,那该多好啊!
而且,按照 \(x,y\) 坐标进行 \(\mathcal{O}(n\log n)\) 排序,再 \(\Theta(n)\) 扫描是完全可行的,这种算法,就被称为 Andrew 算法。
而且好像比 Graham 性能高那么一丢丢 QwQ。
Andrew 算法的步骤
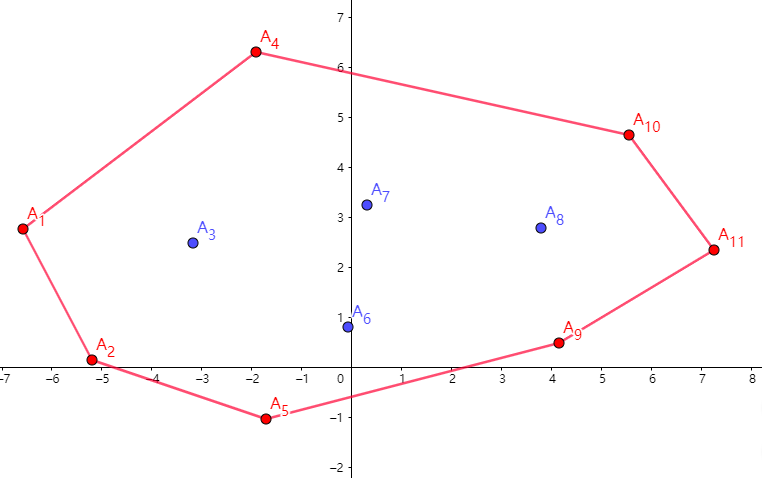
其实 Andrew 算法的步骤与 Graham 是几乎一样的,只是排序的指标不同了(即 Andrew 算法按 \(x\) 为第一关键字,\(y\) 为第二关键字排序;Graham 按极角排序)。如下图:
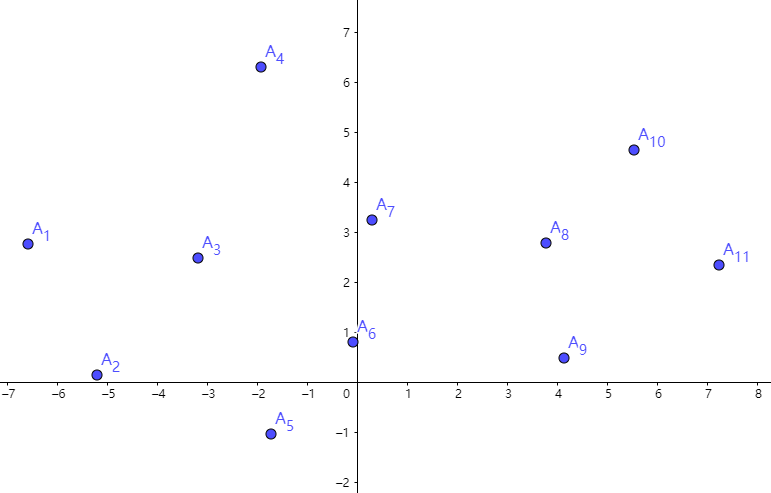
接下来,从 \(A_1\) 开始往右走,找到 \(A_2\),入栈。
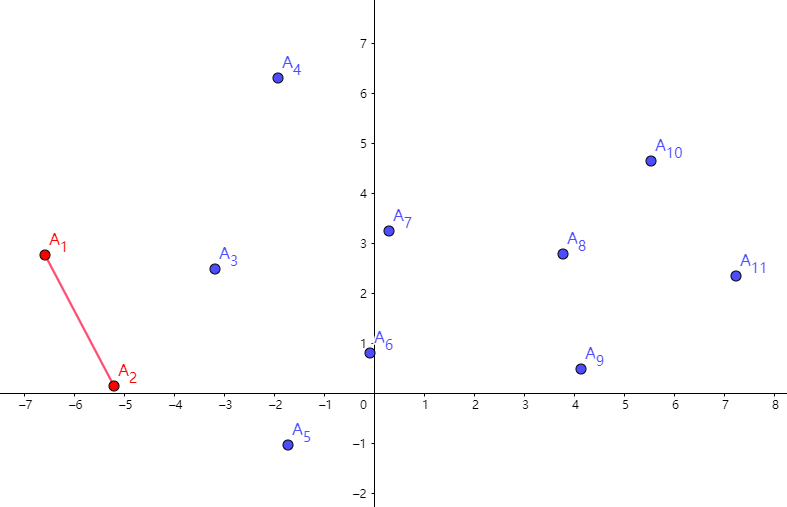
找到了 \(A_3,A_4\),这两点依旧可以形成一个凸壳,入栈。
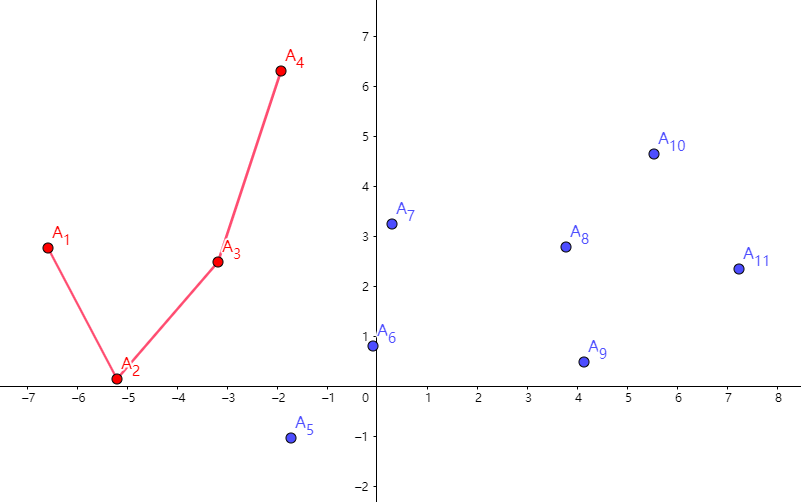
但是,我们接下来扫到了 \(A_5\),它与 \(A_3\) 和 \(A_4\) 都不能形成凸壳,那么就让 \(A_3,A_4\) 出栈,\(A_5\) 入栈。
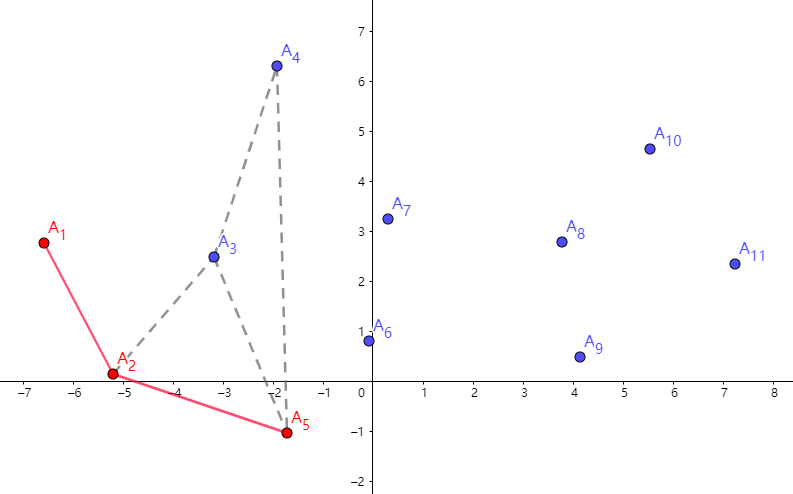
如法炮制,一直向右扫描,找到 \(A_{11}\) 点,我们就会发现:
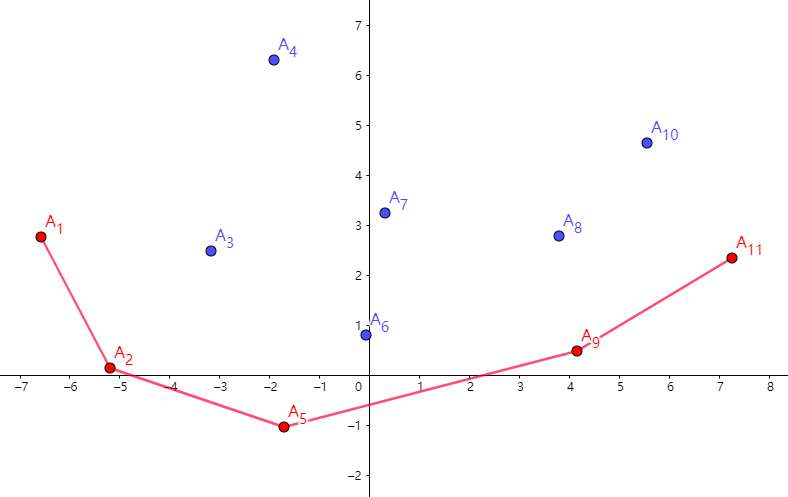
凸包明明还空一半,但是到头了!
但是这不是问题,按照上面的思路,我们当然只能求出凸包的下半部分,如果想要求出凸包的上半部分,就从 \(A_{11}\) 开始往回扫:
先找到 \(A_{10}\) 和 \(A_{8}\)(因为 \(A_9\) 已经在凸包上了,就不用再找了):
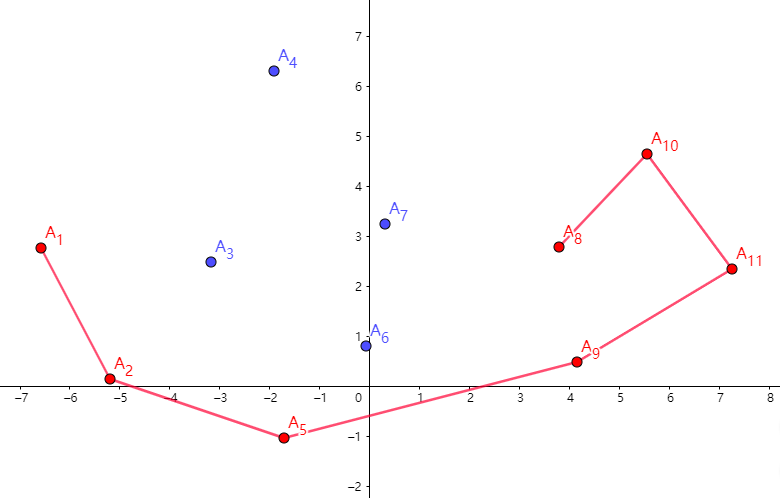
然后 \(A_7,A_6\) 入栈,\(A_8\) 出栈:
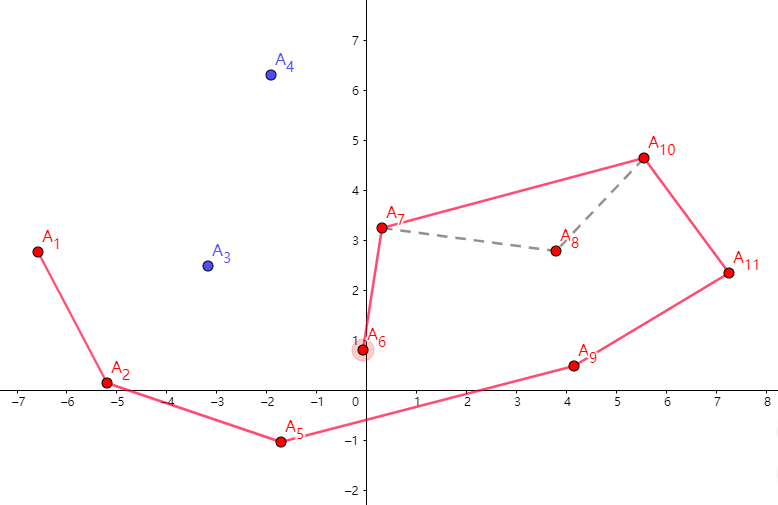
依旧如法炮制,回到 \(A_1\) 点时,我们就获得了整个凸包。
代码
其实与 Graham 算法的代码几乎一样,只需要小小的改动:
#include <algorithm> //使用 swap 函数
#include <cstdio>
#include <cmath> //使用 sqrt 函数
using namespace std;
const int maxN = 100001;
int n, top, stac[maxN]; //手写栈
struct Point {
double x, y;
bool operator < (Point P) { //找到横坐标最小的情况下,纵坐标最小的点
if(x != P.x) {
return x < P.x;
}
else {
return y < P.y;
}
}
} point[maxN];
double tot;
inline double det(Point A1, Point A2, Point B1, Point B2) { //求出向量 <A1,A2> 与 <B1,B2> 的叉积的 z 坐标
return (A2.x - A1.x) * (B2.y - B1.y) - (B2.x - B1.x) * (A2.y - A1.y);
}
inline double dis(Point A, Point B) { //求两点间距离
return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}
int main(void) {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%lf%lf", &(point[i].x), &(point[i].y));
}
sort(point + 1, point + n + 1);
stac[++top] = 1;
for(int i = 2; i <= n; ++i) {
while(top > 1 && det(point[stac[top - 1]], point[stac[top]], point[stac[top]], point[i]) <= 0) { //找到下凹的点就让它出栈
stac[top--] = 0;
}
stac[++top] = i; //i 点入栈
}
for(int i = 1; i < top; ++i) {
tot += dis(point[stac[i]], point[stac[i + 1]]); //计算下凸壳的周长
}
top = 0; //清空栈,开始往回扫
stac[++top] = n;
for(int i = n - 1; i; --i) {
while(top > 1 && det(point[stac[top - 1]], point[stac[top]], point[stac[top]], point[i]) <= 0) { //找到下凹的点就让它出栈
stac[top--] = 0;
}
stac[++top] = i; //i 点入栈
}
for(int i = 1; i < top; ++i) {
tot += dis(point[stac[i]], point[stac[i + 1]]); //计算上凸壳的周长
}
printf("%.2lf", tot);
return 0;
}
//by CaO
时间复杂度分析
Andrew 算法与 Graham 算法一样,都使用了 \(\mathcal{O}(n \log n)\) 预处理,\(\Theta(n)\) 扫描的过程,所以时间复杂度依旧是 \(\mathcal{O}(n\log n)\)。
二维凸包的应用
二维凸包模板并不常在 NOIP 中考察,但是在省选中,它是非常重要的考点。
从它也可以引出计算几何中更加重要的算法,例如旋转卡壳。
除此以外,在一些 dp 题中,有一种名叫斜率优化的时间复杂度优化算法,其中就利用了凸包的知识。
所以,学习二维凸包是有用的,而且是很重要的。
例题
本题目列表会持续更新。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号