【算法笔记】Tarjan 算法 · 下
- 本文总计约 10000 字,阅读大约需要 40 分钟。
前言
上篇笔记的 Tarjan 算法笔记讲了求割点,割边等在无向图中的算法,本篇笔记将会介绍求强连通分量这个在有向图中的理论算法。
强连通分量这个算法大多数情况下在 OI 中不会直接考查,但是它的其它用途非常广泛:例如在部分 dp 题中,需要将一个有环的有向图缩成一个一个的点从而成为一个 DAG(有向无环图),然后再进行拓扑排序。本文除了要介绍强连通分量之外,还要介绍实现上述步骤的方法— —缩点。
顺便,缩点真的是太恶心了,写完代码简直是一口老血喷出来 QAQ
除此以外,笔者还会介绍 Tarjan 算法的另一个应用,求树上的 LCA(最近公共祖先):利用倍增法求 LCA 的时间复杂度为 的预处理以及 的在线查询;而如果用 Tarjan 算法求 LCA,就可以实现 的离线查询。这是非常优秀的时间复杂度优化。
问题引入
小 酷爱探险。一天,他来到了一个巨大的墓室里。这个墓室有 个房间,编号为 ,第 个房间中有价值为 的宝藏。有 条甬道将这 个房间连接起来。然而这个墓室的机关设计得很巧妙,甬道只允许单向通行。现在小 可以从任何一个房间进入墓室,也可以从任何一个房间出来。
小 在盗墓探索墓穴时可以拿走所有他所在房间的宝藏,但是如果重复经过一个房间的话,当然没有两份宝藏给他拿。所以小 想问你,他在离开出口前,至少可以拿走价值为多少的宝藏?
形式化地讲述题目:给定一张有向图 ,点带权,找到一条路径,使经过的节点权值和最大。可以重复经过一个点,但点权只计算一次。
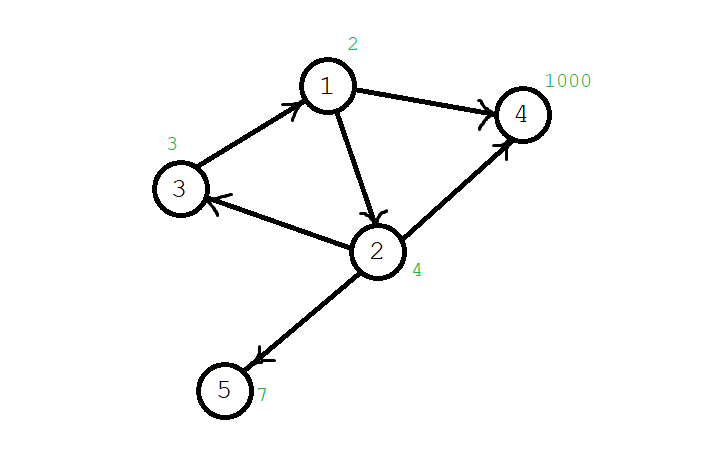
例如:下面这张图中,黑色数字代表房间编号,绿色代表该房间内宝藏的价值。小 可以走路径 1->2->3->1->4,这样获得的最大价值为 。
Tarjan 求强连通分量
求强连通分量的思路及步骤
我们先来复习一下强连通分量的定义:
在一张有向图中,如果我们可以找到若干个结点形成点集 ,使这些节点可以相互到达,则称点集 为图的一个连通分量;同时,若对于某个连通分量 不存在任何一个节点 ,使得 和 依旧形成连通分量,则称 为图的一个强连通分量。
(这个概念好像还是有点太拗口了,但是我也不知道怎么才能简便地描述了 QwQ,我太蒻了)
如果使用 Tarjan 算法的话,依旧可以在 的时间复杂度内求出所有强连通分量,不过与求割点、割边的算法不大相同的,我们需要维护一个节点被搜到的顺序的栈。它的步骤如下:
- 从源点开始搜索。在搜索的时候,将被搜到的节点入栈;
- 维护当前节点的 值和 值。注意维护的方式与割点、割边算法不同:假如目前节点 的出边 指向的节点还在栈内,则我们令 ;
- 在当前节点的所有出边都已经搜完(或者当前节点根本出度为 )的时候回溯,但是不退栈。
- 直到当前回溯到的节点的 值与 值相等的时候,将该节点用一种颜色染色。同时,从栈顶弹出元素,一直到这个节点被弹出,在这个过程中,每个被弹出的节点都要染上相同的颜色。
- 整张图搜完之后,同一个颜色的所有节点,构成一个强连通分量。
好像还是不大好理解 QwQ?我们以下面这张图为例,计算所有的强连通分量。
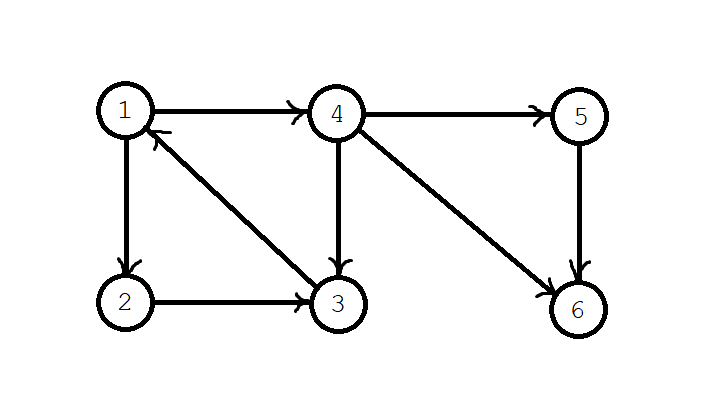
第一步,我们从一号节点开始搜索,,同时,节点 入栈。当前栈序列:;
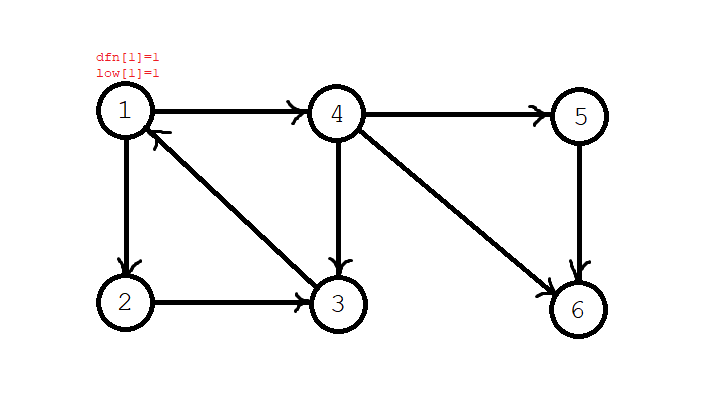
第二步,我们搜到了二号节点,那么 ,节点 入栈。当前栈序列:;
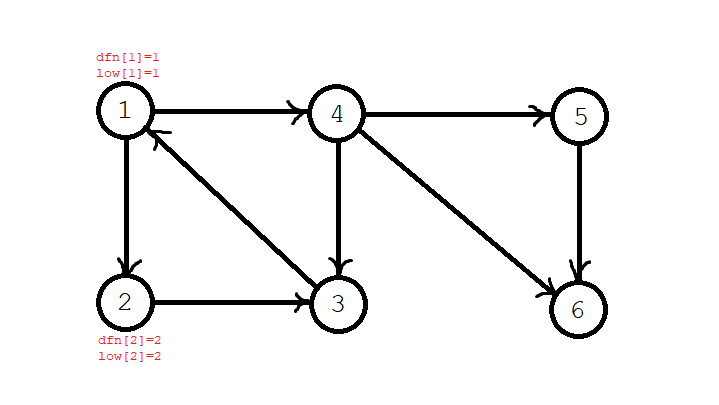
第三步,搜到三号结点的时候,我们发现三号结点可以回到 号节点,所以 ,,节点 入栈,当前栈序列:。
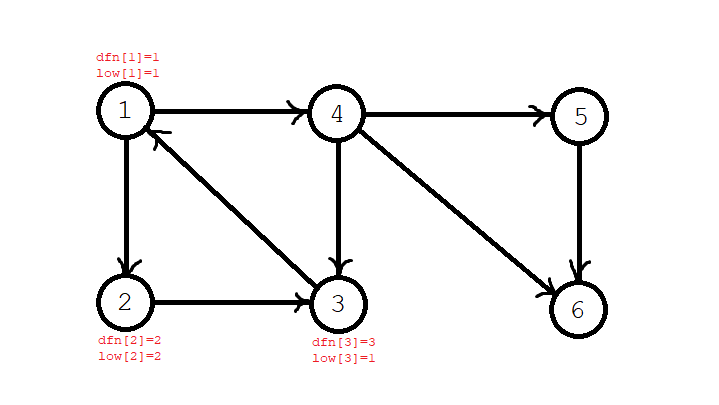
第四步,回溯,但因为 的 和 不相等,这就意味着它可以回到某个 号节点,有可能与 号节点构成强连通分量,所以不退栈。只更新 号节点,。栈序列依旧是:。
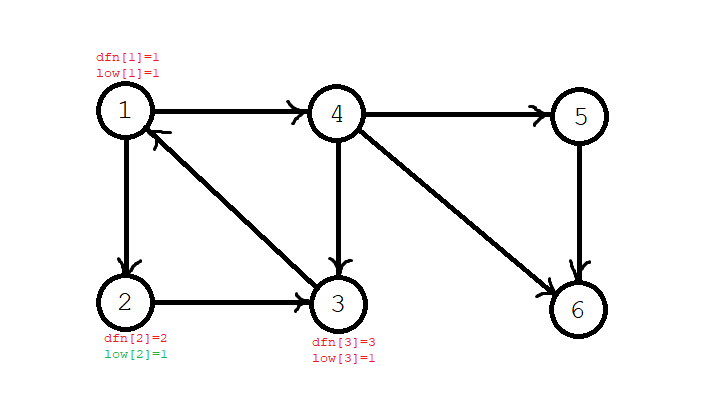
第五步,搜索到 号节点,发现 号结点可以达到 号节点,所以 ,,节点 入栈,当前栈序列:。
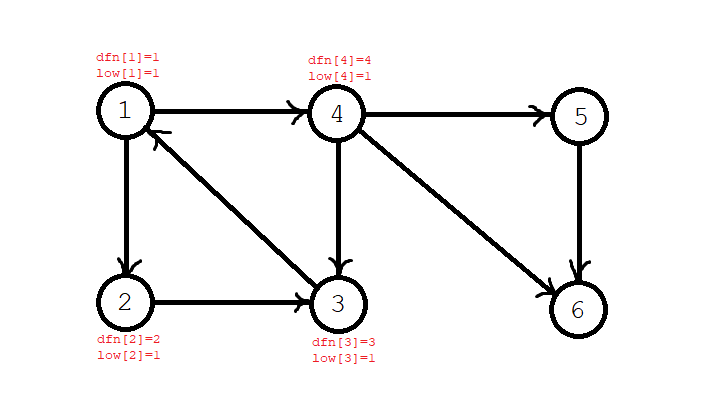
第六步,依次搜索到 号节点,,,节点 入栈,当前栈序列 。
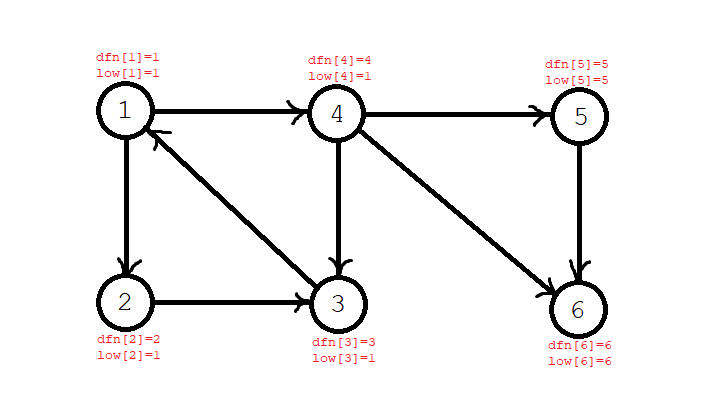
第七步,发现已经搜到头了,回溯,这个时候 ,,说明 和 各自形成一个单独的强连通分量,为它们染色,并将它们退栈。当前栈序列:。
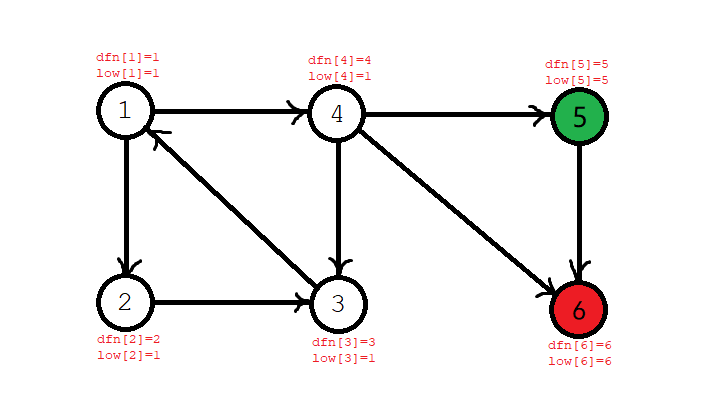
接下来回到 号节点, 号节点找到了 ,但 不在栈里,所以不管它,而且 的 值和 值不相等,所以不将其退栈,栈序列依旧是:。
回溯到 号节点,发现 ,所以 是强连通分量的一个根,从栈顶弹出元素,直到 被弹出,这个时候,为所有弹出元素染色。
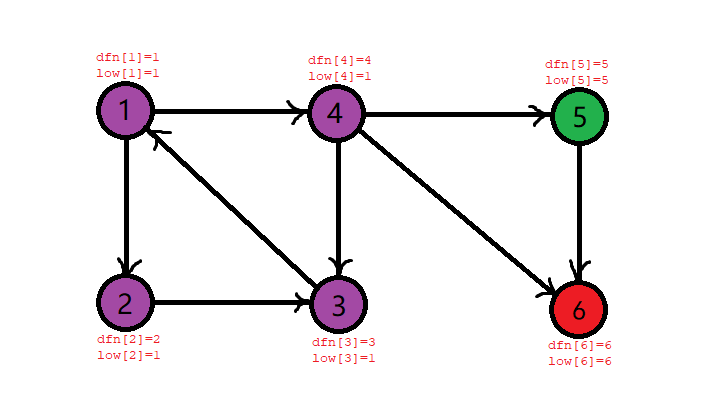
就这样,所有的颜色相同的节点,就构成了一个强连通分量,我们就找到了整张图中所有的强连通分量。
代码
依旧是模拟上述步骤:
#include <cstdio>
#include <stack>
using namespace std;
const int maxN = 2000001;
int top, n, m, cur, tot;
int head[maxN], dfn[maxN], low[maxN], color[maxN];
bool vis[maxN];
stack <int> stac; //这里用了 STL,如果追求高性能,请使用手写栈或 O2 优化
struct Edge {
int to;
int next;
} edge[maxN];
inline void add_edge(int u, int v) {
edge[++top].to = v;
edge[top].next = head[u];
head[u] = top;
}
void tarjan(int u) { //Tarjan 求强连通分量
dfn[u] = low[u] = ++cur;
vis[u] = true;
stac.push(u); //每次搜索新的节点就将其入栈
for(int ptr = head[u]; ptr; ptr = edge[ptr].next) {
int curv = edge[ptr].to;
if(!dfn[curv]) {
tarjan(curv);
low[u] = min(low[u], low[curv]); //通过孩子结点更新 low 值
}
else if(vis[curv]) { //如果找到的节点不在栈中,意味着这个节点已经位于强连通分量中了,不用再更新 low 值了
low[u] = min(low[u], low[curv]);
}
}
if(dfn[u] == low[u]) { //dfn[u] == low[u] 就意味着这个点是强连通分量分一个“根”节点
color[u] = ++tot; //染色
vis[u] = false; //退栈操作
while(stac.top() != u) {
color[stac.top()] = tot;
vis[stac.top()] = false;
stac.pop();
}
stac.pop();
}
}
int main(void) {
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_edge(ui, vi);
}
for(int i = 1; i <= n; ++i) {
if(!dfn[i]) { //有向图不一定是强连通图
tarjan(i);
}
}
for(int i = 1; i <= n; ++i) {
printf("%d ", color[i]); //输出每个点所在的强连通分量的编号
}
return 0;
}
//by CaO
缩点— —强连通分量的应用
缩点的用途
回到题目引入中的问题:
假如说题目中的墓室里所有的门都不能回到已经走过的墓室,那么基于贪心的思想:我们应该会选择从前面没有房间的房间进入,到无路可走的房间离开— —如果你从一个前面还有房间的地方进入,那你为什么不在前一个房间进呢。
这样的话,我们首先想到的就是拓扑排序:每次都找到入度为 的节点,删去这些点,并对它们的 “子” 节点进行记忆化搜索。(如果有时间我会开一个坑,着重讲一下拓扑排序 QwQ,不过现在还是懒)
然而,题目并没有保证这张图是一个 DAG(有向无环图),所以,直接使用拓排,如果遇见了环,就会得到 “无解” 的答案。
我们会想,如果有若干个点连成了一个强连通分量,那么依旧是基于贪心的思想,我们当然是将这个强连通分量里的所有点都走一遍,能拿干嘛不拿。
既然如此,所有的强连通分量,就等效于一个个的点,这个点的权值,就是强连通分量里所有点的权值和,如下图。
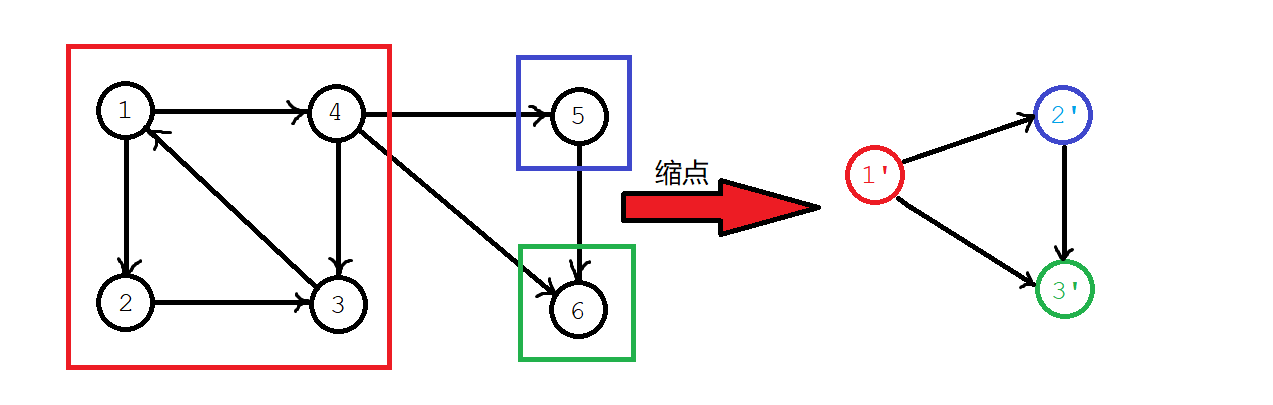
这样,我们在找到所有的强连通分量后,把它们缩环为点,就可以得到一张 DAG,我们就可以在这上面进行拓排辣!QwQ
代码
说实在的,这个代码我真是不想贴上了,写得我神清气爽,终于把洛谷上的板子题 A 了,但是因为写得太乱了,实在是不敢优化 QwQ,凑合着看吧。
/***写完了连自己都不敢调的缩点 QAQ***/
#include <cstdio>
#include <stack>
#include <queue>
using namespace std;
const int maxN = 2000001;
int top, n, m, cur, tot, ans;
int head[maxN], newhead[maxN];
int dfn[maxN], low[maxN];
int fa[maxN], color[maxN], index[maxN];
int dp[maxN], arr[maxN];
bool vis[maxN];
stack <int> stac;
queue <int> que;
struct Edge {
int to;
int next;
} edge[maxN], newedge[maxN];
inline void add_edge(int u, int v) {
edge[++top].to = v;
edge[top].next = head[u];
head[u] = top;
}
inline void add_new(int u, int v) {
newedge[++top].to = v;
newedge[top].next = newhead[u];
newhead[u] = top;
}
void tarjan(int u) { //Tarjan 求强连通分量
dfn[u] = low[u] = ++cur;
vis[u] = true;
stac.push(u); //每次搜索新的节点就将其入栈
for(int ptr = head[u]; ptr; ptr = edge[ptr].next) {
int curv = edge[ptr].to;
if(!dfn[curv]) {
tarjan(curv);
low[u] = min(low[u], low[curv]); //通过孩子结点更新 low 值
}
else if(vis[curv]) { //如果找到的节点不在栈中,意味着这个节点已经位于强连通分量中了,不用再更新 low 值了
low[u] = min(low[u], low[curv]);
}
}
if(dfn[u] == low[u]) { //dfn[u] == low[u] 就意味着这个点是强连通分量分一个“根”节点
color[u] = ++tot; //染色
vis[u] = false; //退栈操作
while(stac.top() != u) {
color[stac.top()] = tot;
vis[stac.top()] = false;
fa[stac.top()] = u;
stac.pop();
}
stac.pop();
}
}
void toposort(void) {
for(int i = 1; i <= n; ++i) {
if(index[fa[i]] == 0 && !vis[fa[i]]) {
vis[fa[i]] = true;
dp[fa[i]] = arr[i];
ans = max(dp[fa[i]], ans); //用入度为 0 的点更新 ans 值
que.push(fa[i]); //入度为 0 的点入栈
}
}
while(!que.empty()) { //拓扑排序模板
int curu = que.front();
que.pop();
for(int ptr = newhead[curu]; ptr; ptr = newedge[ptr].next) {
int curv = newedge[ptr].to;
--index[curv];
if(!index[curv]) {
que.push(curv);
}
dp[curv] = max(dp[curv], dp[curu] + arr[curv]); //每次更新节点的 dp 值时更新答案。
ans = max(ans, dp[curv]);
}
}
}
int main(void) {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i) {
scanf("%d", &arr[i]);
fa[i] = i;
}
for(int i = 1; i <= m; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_edge(ui, vi);
}
top = 0;
for(int i = 1; i <= n; ++i) {
if(!dfn[i]) { //有向图不一定是强连通图
tarjan(i);
}
}
for(int i = 1; i <= n; ++i) {
if(fa[i] != i) {
arr[fa[i]] += arr[i]; //缩点
}
for(int ptr = head[i]; ptr; ptr = edge[ptr].next) { //建立新图
if(fa[edge[ptr].to] != fa[i]) {
add_new(fa[i], fa[edge[ptr].to]);
++index[fa[edge[ptr].to]];
}
}
}
toposort(); //拓扑排序
printf("%d", ans); //输出可获得的最大权值和
return 0;
}
//by CaO
Tarjan 与 LCA 算法
LCA 问题介绍
所谓 LCA,即树上最近公共祖先(Least Common Ancestors)。问题内容是:给定一棵有 个结点的有根树,结点编号为 。 次询问编号为 的一对节点在树上最近的一级公共祖先为哪个点。
Tarjan 算法求 LCA
Tarjan 算法可以在 的预处理, 查询的复杂度内完成 LCA 的离线算法。算法过程如下:
- 保存所有需要查询的点对编号;
- 从根节点开始搜索这棵树,在搜索某个点的时候将其标记为已访问过;并在回溯时将它的所有孩子结点与之合并(这里需要使用并查集);
- 遍历所有与当前节点 有查询关系的节点 ,如果 已经被访问过,那么我们输出 和 的 LCA 为 。
还是上图,以这张图为例,求 (为了方便表示,标记节点被访问过的操作在以下视为染成绿色):
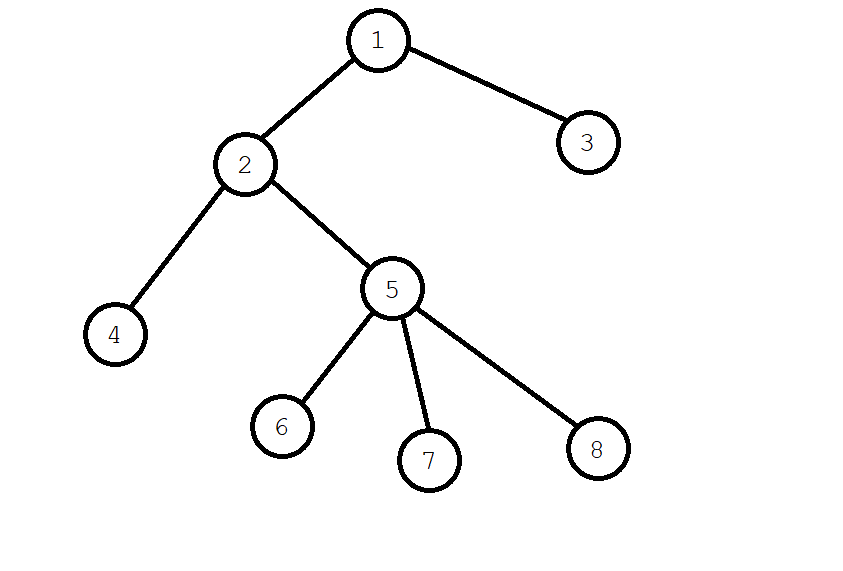
从一号节点开始搜索,一号节点染色,并递归搜索 号节点。
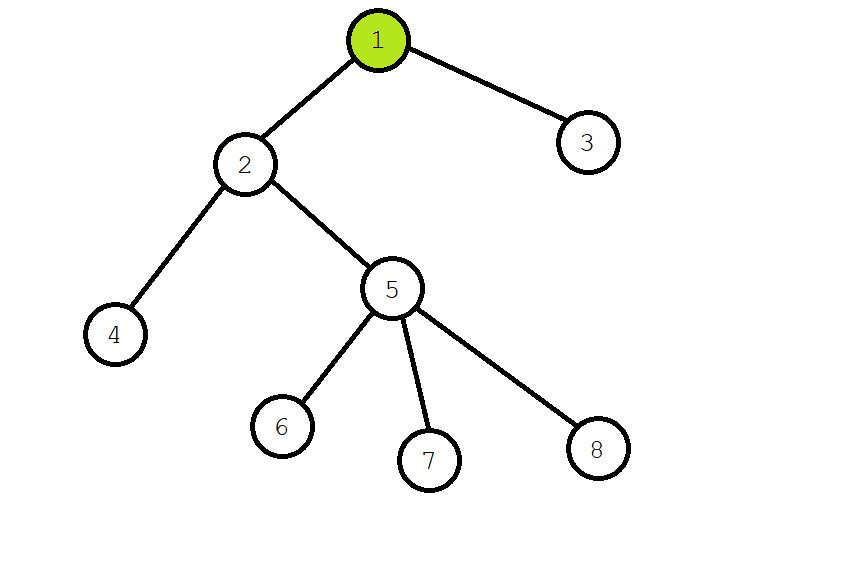
二号节点染绿后,遍历它的子树,遇见四号结点。与四号结点有查询关系的是 ,但其未被查询到,不管它。
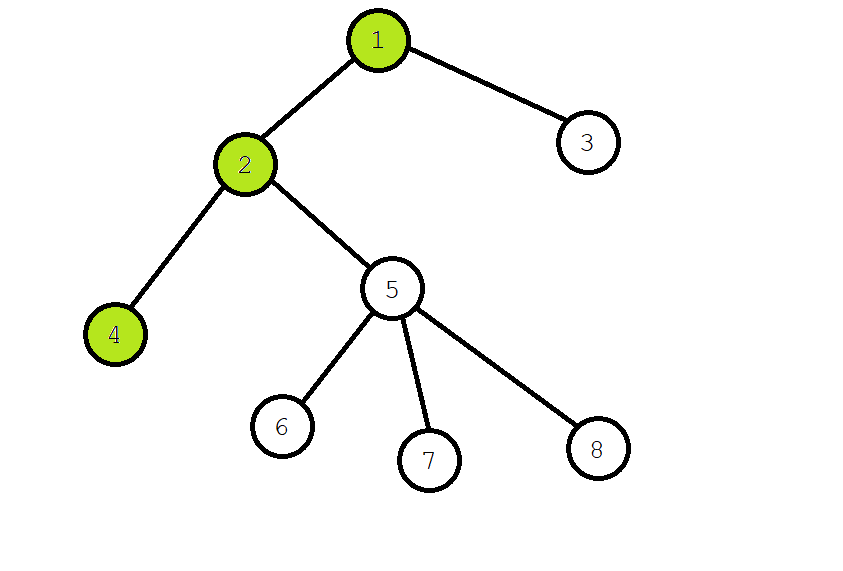
回溯的时候,把四号结点和二号节点合并。
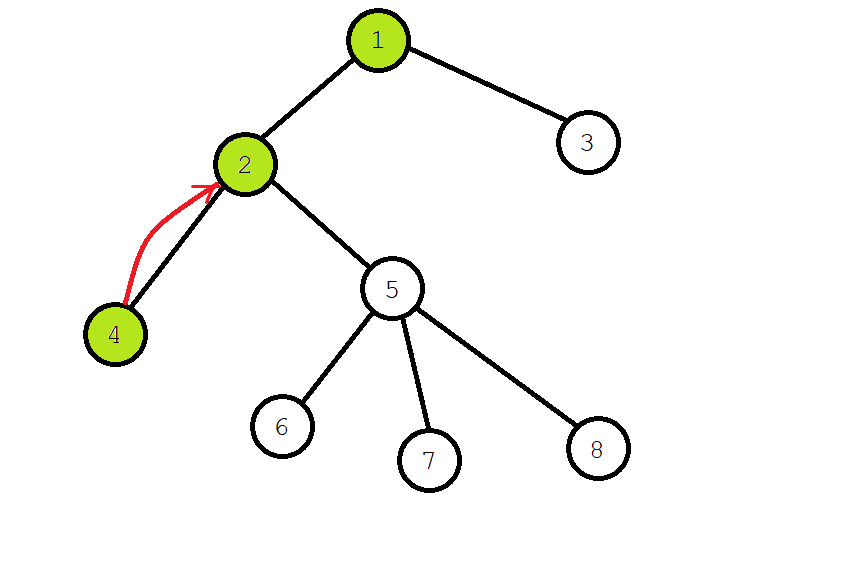
再搜索 的另一棵子树,给 号染色,递归找到 号节点,并给 号染色。
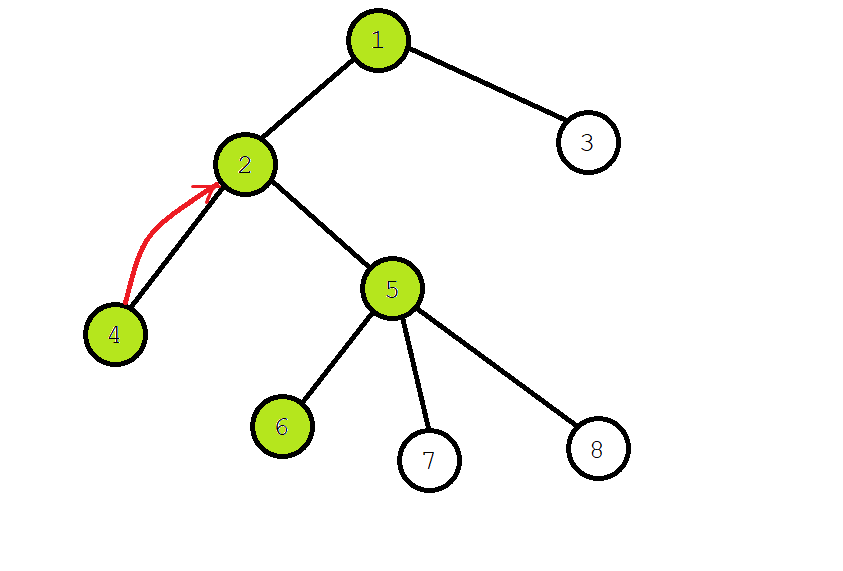
我们发现 与 有查询关系,而且 已经被访问过了,所以我们可以知道 。
像这样的算法,可以在一遍 DFS 内找出任意两个节点的 LCA,与倍增相比更要高效。可以尝试着自己动笔模拟一下。
代码
#include <cstdio>
using namespace std;
const int maxN = 200001;
int head[maxN], query[maxN], fa[maxN];
int n, m, top;
bool isRoot[maxN], vis[maxN], answered[maxN];
struct Edge {
int to;
int next;
int num;
} edge[maxN], ans[maxN]; //edge 记录原树,answer 记录所有待查询的点对
inline void add_edge(int u, int v) {
edge[++top].to = v;
edge[top].next = head[u];
head[u] = top;
}
inline void add_query(int u, int v, int num) { //添加查询队伍
ans[++top].to = v;
ans[top].next = query[u];
ans[top].num = num;
query[u] = top;
}
//并查集模板
inline void init(int n) {
for(int i = 1; i <= n; ++i) {
fa[i] = i;
isRoot[i] = true;
}
}
int find(int x) {
if(fa[x] == x) {
return x;
}
else {
fa[x]=find(fa[x]);
return fa[x];
}
}
inline void merge(int x, int y) {
fa[find(x)] = find(y); //注意合并的方向是 x 并向 y
}
void tarjan(int x) {
vis[x] = true; //标记该点已访问过
for(int ptr = head[x]; ptr; ptr = edge[ptr].next) {
int curv = edge[ptr].to;
tarjan(curv);
merge(curv, x); //合并孩子结点
}
for(int ptr = query[x]; ptr; ptr = ans[ptr].next) {
int curv = ans[ptr].to, num = ans[ptr].num;
if(vis[curv] && !answered[num]) {
printf("LCA(%d, %d) = %d\n", x, curv, find(curv)); //离线输出答案
answered[num] = true; //同一个问题不用回答两次
}
}
}
int main(void) {
scanf("%d%d", &n, &m);
init(n);
for(int i = 1; i < n; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_edge(ui, vi);
isRoot[vi] = false;
}
top = 0;
for(int i = 1; i <= m; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_query(ui, vi, i);
add_query(vi, ui, i);
}
for(int i = 1; i <= n; ++i) {
if(isRoot[i]) { //从根节点开始 DFS
tarjan(i);
}
}
return 0;
}
//by CaO
例题
本题目列表会持续更新。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】