【算法笔记】Tarjan 算法 · 上
- 本文总计约 8300 字,阅读大约需要 30 分钟。
前言
Tarjan 算法也是一个非常经典的算法了,因为它所涉及的名词实在是太多了,而且算法本身也很抽象,所以我学习的时候也是慢吞吞的。所以各个地方瞎看瞎看着,也算是勉勉强强地学会了。而且看网上大部分的博客,讲得都不甚详细,所以自己也想尽量写一篇更加详细的博客。虽然还是会有诸多不足,但我还是会尽力地把它讲明白的 QwQ。
因为 Tarjan 算法涵盖的内容太多了,包括割点,桥,强连通分量等多个问题,所以我会用两篇文章介绍它。上篇将讲较简单的割点和桥,下篇将介绍相对复杂的强连通分量。
题目引入
国的交通系统非常发达,这个国家有 个城市,编号为 。并且有 条双向通行的公路,每条道路都将两个城市连接起来,且所有的 条道路将这些城市连接在一起,即任意两个城市都可以通过公路相互抵达。
现在, 国的敌国与 国开战了。他们知道如果炸毁某一个城市,那么与这个城市相连的公路的交通,也会随即切断。所以他们要派遣飞机炸毁其中的一个城市,以达到切断 国交通系统的目的。即通过炸毁一个城市之后,有两个城市不能通过公路相互抵达。你是敌国的参谋,请问应该如何选择城市,才能达到目的呢?
形式化地讲述题面:给定一张无向图 ,求图的割点,其中 ,。
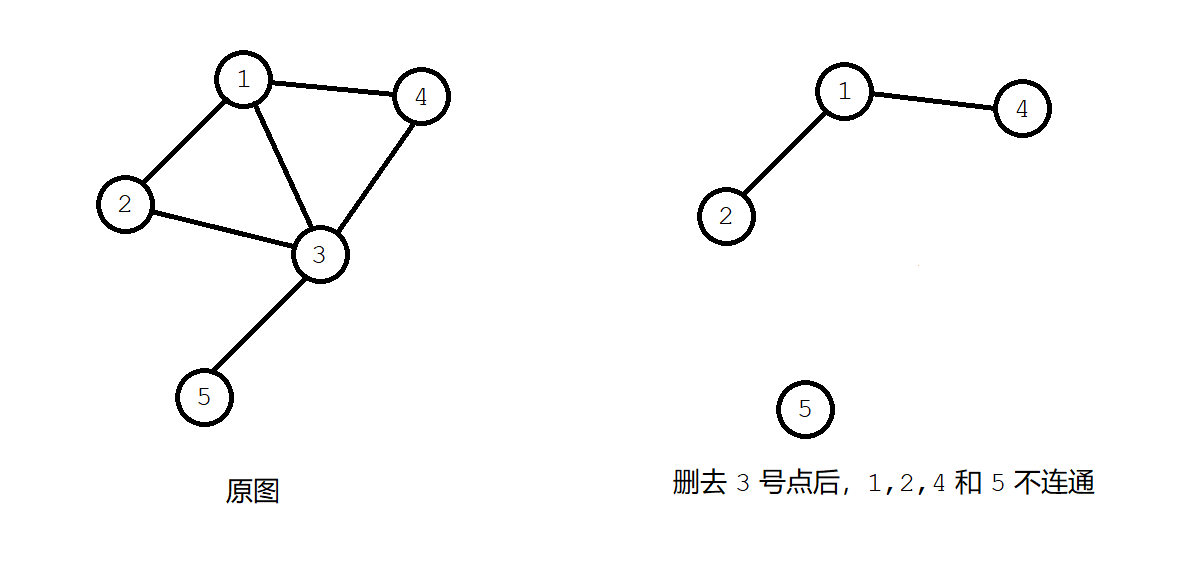
例如:以下这张图的割点即为 号点。因为删去 号点之后图不再连通。
基本定义
- 割点:在一张无向图中,删去某个点以及与之相邻的所有边后,图不再连通,则称这个点为割点。如上图中, 号点即为割点;
- 割边:在一张无向图中,删去某一条边后,图不再连通,则称这条边为割边,又称桥。如下图,标红的边为割边:
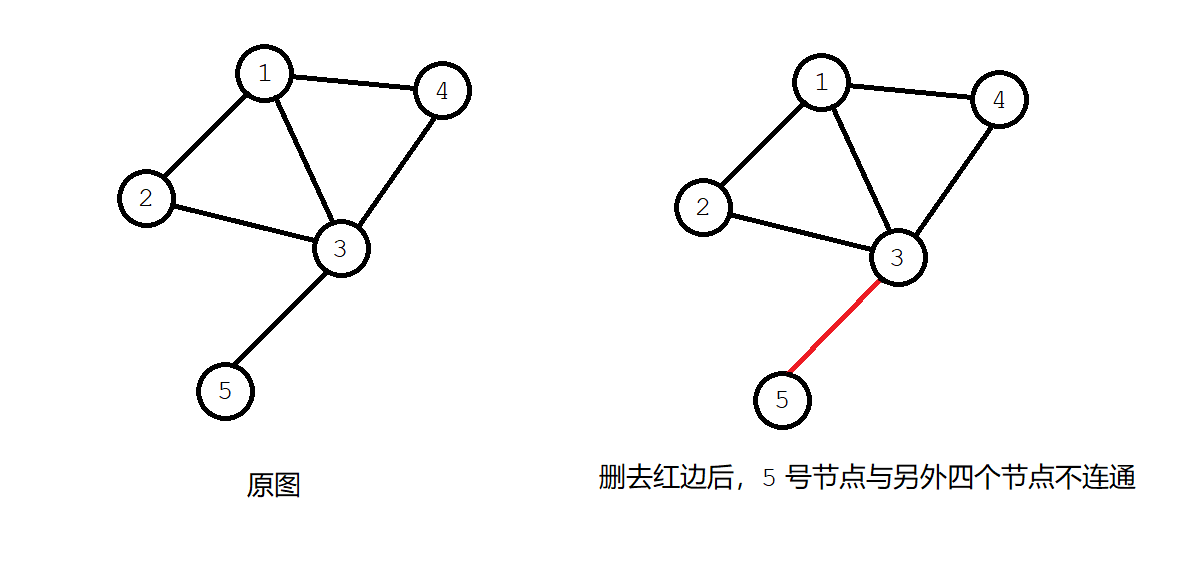
- 强连通分量:在一张有向图中,如果我们可以找到若干个结点形成点集 ,使这些节点可以相互到达,则称点集 为图的一个连通分量;同时,若对于某个连通分量 不存在任何一个节点 ,使得 和 依旧形成连通分量,则称 为图的一个强连通分量。如下图,,则称 为图的一个强连通分量:
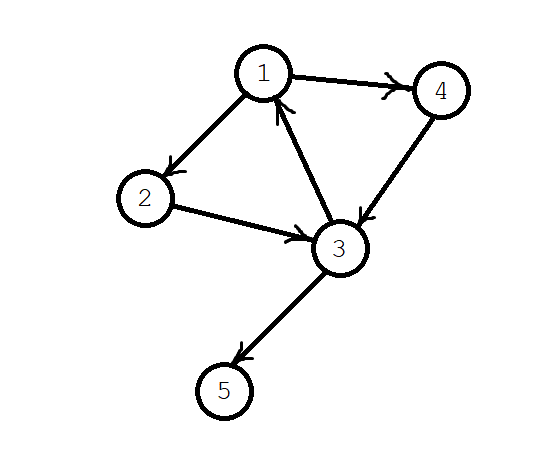
暴力求割点的思路及缺陷
依照惯例,我们最先当然是要想:暴力怎么做?
当然可以这么做:枚举删去每一个结点,然后用 DFS 跑一遍整张图,如果这张图的其余所有节点不能跑完,那么这个点就是割点;否则就不是割点。
代码如下:
#include <iostream>
#include <cstring> //使用 memset 函数
using namespace std;
const int maxN=2000001;
int head[maxN], top, n, m, cnt;
bool vis[maxN], isCut[maxN]; //isCut[i] 代表 i 是不是割点
//链式前向星模板
struct Edge {
int to;
int next;
} edge[maxN];
inline void add_edge(int u, int v) {
edge[++top].to = v;
edge[top].next = head[u];
head[u] = top;
}
bool dfs(int cur, int fa) { //枚举每一个结点进行 DFS,fa 代表是从哪个节点开始搜索的
int nxt = 0; //计数器,统计从 fa 结点直接搜索了多少个“子”节点,若 nxt>1,则意味着该节点是割点
vis[cur] = true;
for(int ptr = head[cur]; ptr; ptr = edge[ptr].next) {
int curv = edge[ptr].to;
if(!vis[curv]) {
++nxt;
dfs(curv, fa);
}
}
if(cur == fa && nxt > 1) {
return true;
}
else {
return false;
}
}
int main(void) {
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_edge(ui, vi);
add_edge(vi, ui);
}
for(int i = 1; i <= n; ++i) {
memset(vis, 0, sizeof(vis)); //初始化 vis 数组
isCut[i] = dfs(i, i);
if(isCut[i]) {
++cnt;
}
}
printf("%d\n", cnt); //输出图中有多少个割点
for(int i = 1; i <= n; ++i) {
if(isCut[i]) {
printf("%d ", i); //从小到大输出所有割点的编号
}
}
return 0;
}
//by CaO
如此优雅的代码,那么它的性能如何呢?
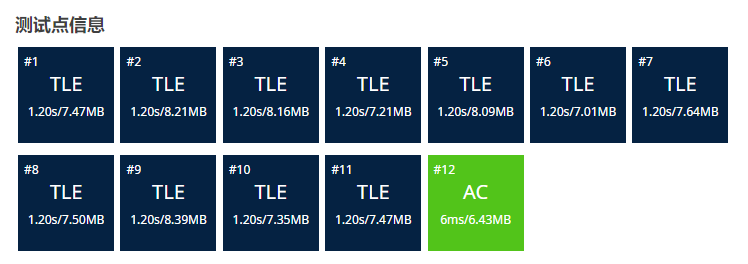
看上去并不大好……
这道题是洛谷 P3388【模板】割点(割顶),求割点的板子题。然而即使是开了 优化,也拿到了 个点超时了 个点的好成绩。
事实上,其时间复杂度为 ,这道题中 ,,当然是妥妥的超时了 QwQ。
但是我们发现,对每一个结点都跑一遍 DFS,实在是有些太浪费时间了,如果有一种算法,能够在一遍 DFS 后就能找到所有的割点就好了,这样的算法就可以将时间复杂度降到 。
而这,就是我们接下来要学习的 Tarjan 算法。
Tarjan 算法
Tarjan 算法的引入及介绍
Tarjan 算法,顾名思义,是由计算机科学家 发明的算法。而为了介绍这个算法,我们需要先介绍一些名词:
- DFS 搜索树:我们通过在图上深度优先搜索,保留其中所有在遍历过程中经过的边,将这些边连起来,就会形成一棵树。例如下图:从 号节点出发,跑 DFS 的顺序为 1->2->3->4->3(回溯)->5,故其 DFS 搜索树如下右图红边所示,其根节点为 。
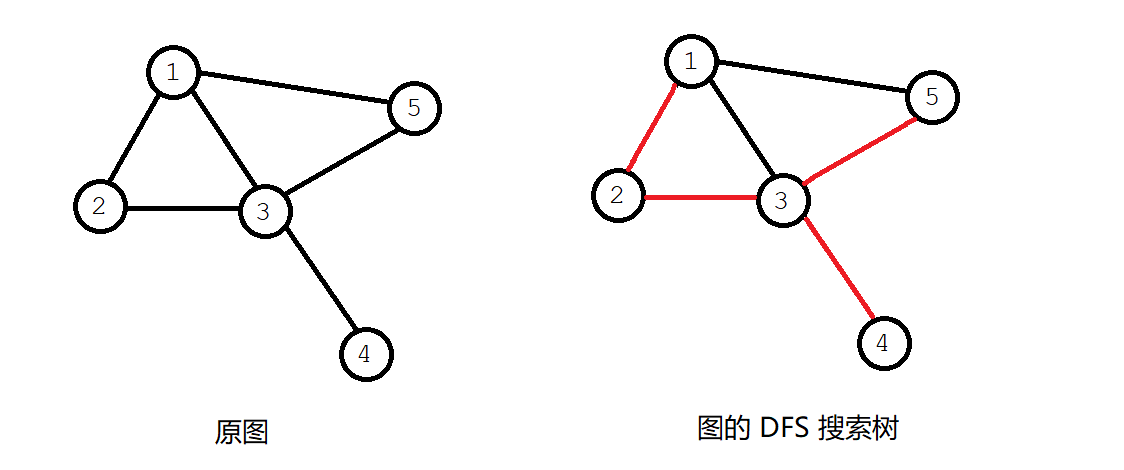
同时,我们称其中的红边,即直接连接搜索树上的父子两点的边为出边,类似 , 的两条边,它们并不在 DFS 搜索树中被经过,而这种从某个节点回到其祖先节点的边为回边。
-
时间戳:在图的 DFS 中, 号节点被访问到的排名,被称为其时间戳,以下记作 ,例如上图中, 号节点是第一个被访问的, 号节点是第二个被访问的……以此类推。所以有 ,,,,。
-
追溯值:在图被 DFS 后,生成了一个 DFS 搜索树。 号节点通过绕过其父结点能够回到的时间戳最小的节点的时间戳,称为其追溯值,以下记作 。注意,这里说的绕过父结点,既可以是通过回边,也可以是通过其孩子节点回到某个节点(这句话依旧非常拗口 QwQ,既然概念非常难懂,请读者多读几遍)。
例如上图, 号节点是 号节点的父结点,但 号节点能够通过回边 回到 号节点,故 ,同理 ;
而 号节点虽然本身不能回到 号节点,但它可以通过路径 回到 号节点,故 ;
然而, 号节点不能绕过 号节点回到任何节点,故它只能追溯到其本身,故有 。
Tarjan 算法的 DFS 过程
我们为什么要大费周章地介绍上面的三个概念呢?因为接下来生成一个 Tarjan 图(笔者喜欢这样称呼它 QwQ,不要介意)就需要我们知道,如何计算每个节点的 值和 值。
算法过程大致如下:从根节点开始搜索。每次搜索到一个新的节点 ,我们就可以很容易地得到该点 值,同时,令该点的 。接下来,从这个点继续搜索,如果搜索到一个比该点时间戳小的结点 ,那么就令 ;如果搜索到一个新的节点 ,那么就对 重复上述操作,并在回溯时,令 。
当然,直接描述看起来很抽象。所以我们以下面这张图为例,我们来计算一下每个点的 和 :
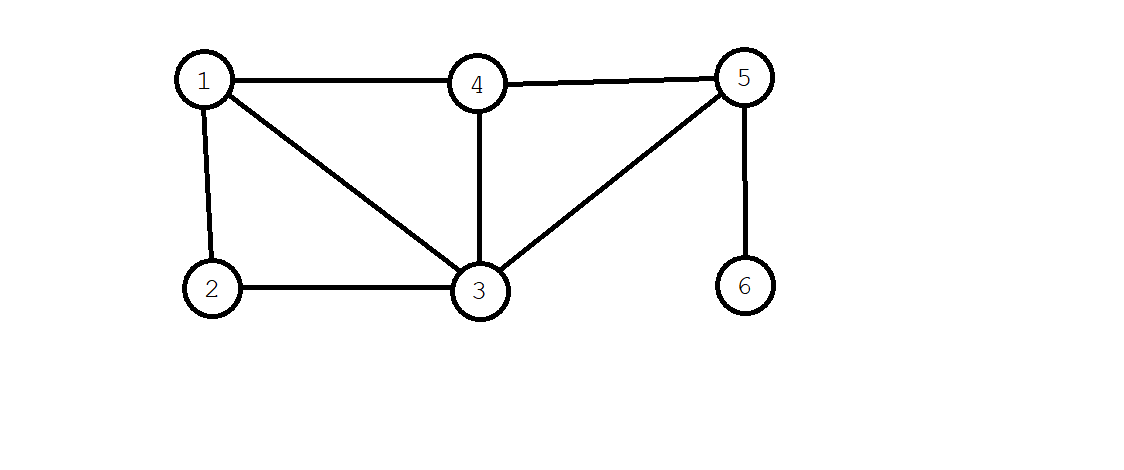
- 我们既然是从 号节点开始搜索,那么一定有 。
- 第二个搜到的是 号节点,则 ;第三个是 号节点,,如下图:
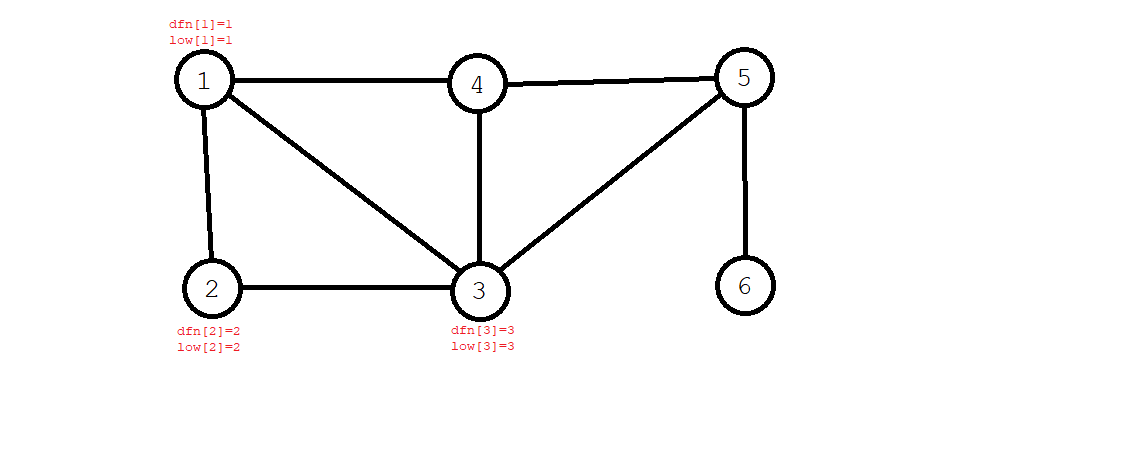
- 然而,从 号节点,我们可以回到 号节点,所以我们要更新 。
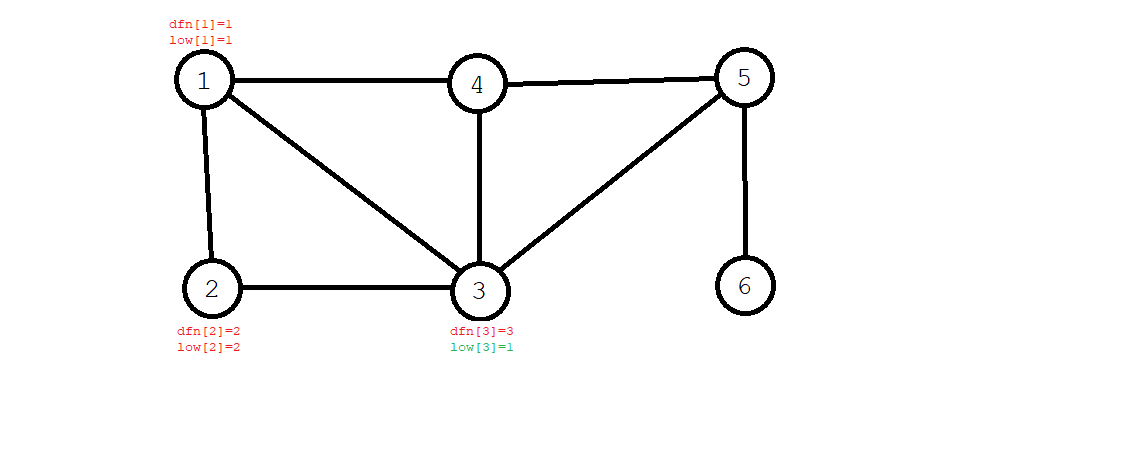
- 第四个搜到的是 号节点,,同时,因为 号节点能够回到 号节点,也有 。
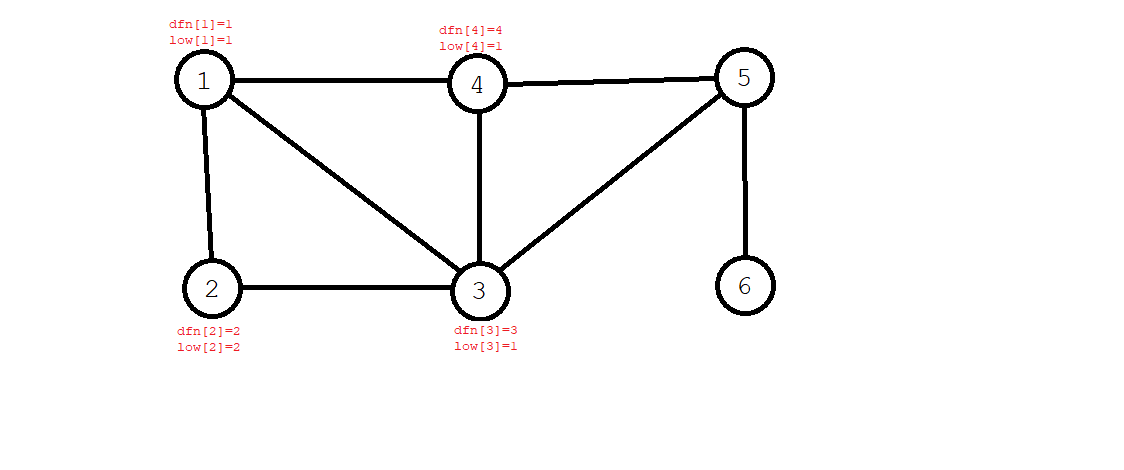
- 第五个搜到的是 号节点, 号节点可以回到 号节点,故 。第六个搜到了 号节点,这个节点不能回到任何一个结点,故 。
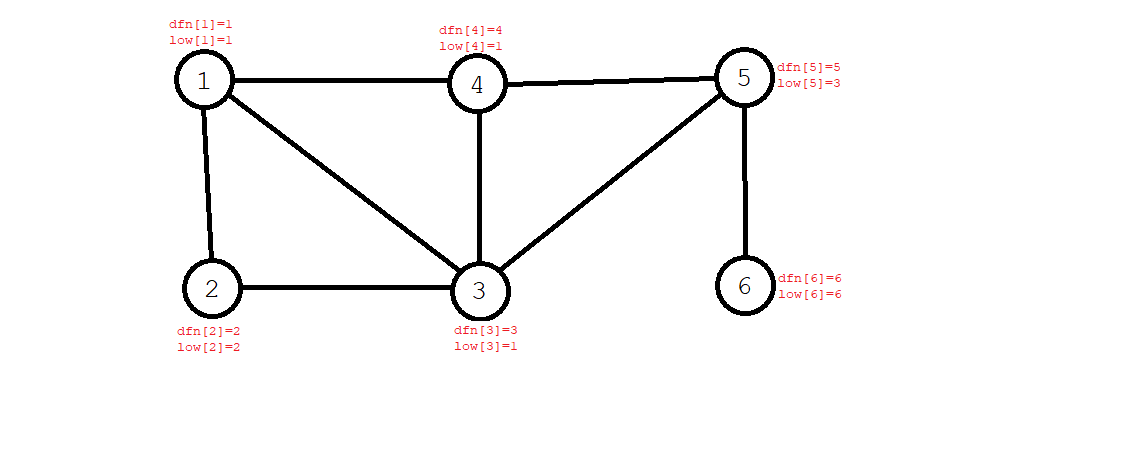
- 一直回溯,回溯到二号节点时,发现其孩子结点 号的 ,故 。
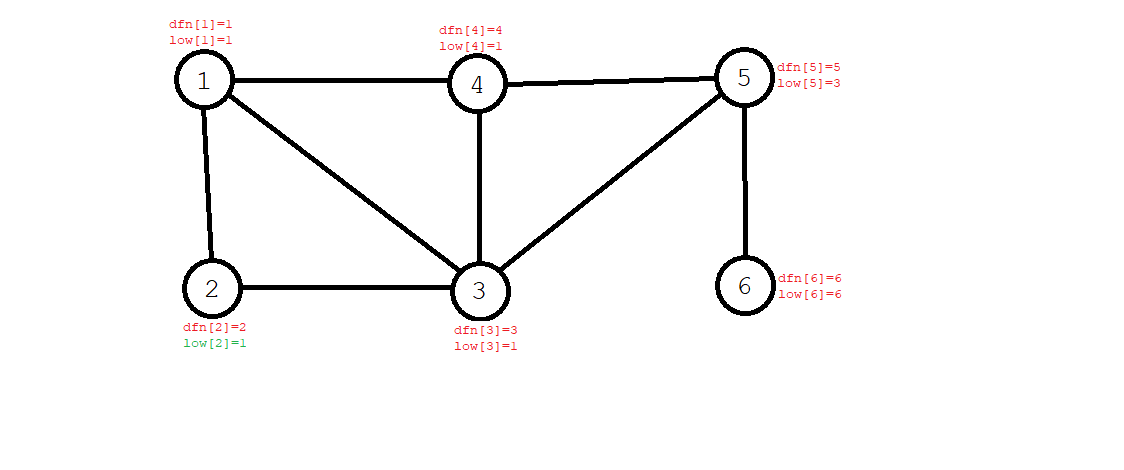
通过上述步骤,我们得到了每个节点的 和 值。
代码就模拟上述步骤实现就可以:
#include <iostream>
using namespace std;
const int maxN=2000001;
int head[maxN], top, n, m, cnt;
int dfn[maxN], low[maxN];
struct Edge {
int to;
int next;
} edge[maxN];
inline void add_edge(int u, int v) {
edge[++top].to = v;
edge[top].next = head[u];
head[u] = top;
}
void tarjan(int cur, int fa) {
dfn[cur] = low[cur] = ++cnt;
for(int ptr = head[cur]; ptr; ptr = edge[ptr].next) {
int curv = edge[ptr].to;
if(!dfn[curv]) {
tarjan(curv, fa); //对未访问的结点进行深搜
low[cur] = min(low[cur], low[curv]); //在回溯时更新 low 值
}
low[cur] = min(dfn[cur], low[curv]); //通过回边更新 low 值
}
}
int main(void) {
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_edge(ui, vi);
add_edge(vi, ui);
}
for(int i = 1; i <= n; ++i) {
printf("%d ", dfn[i]); //依次输出每个点的 dfn 值
}
putchar('\n');
for(int i = 1; i <= n; ++i) {
printf("%d ", low[i]); //依次输出每个点的 low 值
}
return 0;
}
//by CaO
Tarjan 求割点和桥
Tarjan 求割点的做法很简单,对于一张图的 DFS 搜索树,如果这棵树上某个非根节点 ,存在它的一个一级孩子结点 ,满足 ,那么就有 是一个割点。
证明也很显然,如果 ,就意味着在 在不回到其父亲节点的情况下,哪里也去不了。
如果是 是根节点呢?也很简单,统计它的子树数量 ,如果 ,就说明根节点的子树们在不经过根节点的情况下不能相互抵达。
上代码:
#include <iostream>
#define reg register
using namespace std;
const int maxN=200001;
int n, m, head[maxN], dfn[maxN], low[maxN];
int cnt, top, tot;
bool isCut[maxN];
struct Edge{
int to;
int next;
} edge[200001];
inline void add_edge(int u, int v) {
edge[++top].to=v;
edge[top].next=head[u];
head[u]=top;
}
void tarjan(int u, int fa) { //Tarjan 算法求割点
int child=0; //统计以当前节点为根的子树个数
low[u]=dfn[u]=++cnt;
for(reg int ptr=head[u]; edge[ptr].to; ptr=edge[ptr].next) {
int cur=edge[ptr].to;
if(!dfn[cur]) {
tarjan(cur, u); //对未访问的结点进行深搜
low[u]=min(low[u], low[cur]); //在回溯时更新 low 值
if(u==fa) {
++child;
}
if(low[cur]>=dfn[u] && u!=fa) {
isCut[u]=true;
}
}
low[u]=min(low[u], dfn[cur]); //通过回边更新 low 值
}
if(child>1 && u==fa) {
isCut[u]=true; //如果该根节点的子树多于一棵,则说明根节点是割点
}
}
int main(void) {
scanf("%d%d", &n, &m);
for(reg int i(1); i<=m; ++i) {
int ui, vi;
scanf("%d%d", &ui, &vi);
add_edge(ui, vi);
add_edge(vi, ui);
}
for(reg int i(1); i<=n; ++i) {
if(!dfn[i]) {
tarjan(i, i); //注意图不一定连通
}
}
for(reg int i(1); i<=n; ++i) {
if(isCut[i]) {
++tot;
}
}
printf("%d\n", tot); //输出割点的个数
for(reg int i(1); i<=n; ++i) {
if(isCut[i]) {
printf("%d ", i); //输出所有割点的编号
}
}
return 0;
}
//by CaO
Tarjan 算法求割边
对于图中的每一条边,若它所连接的两个结点 和 满足 ,则意味着这条边是割边。因为 ,就意味着 不能通过这条边到达 。代码留给读者作为练习。
时间复杂度分析
Tarjan 算法只需要通过一遍 DFS 就能求出所有的割点和桥,以及强连通分量(下回将会提出如何求图的强连通分量)。所以它的时间复杂度即为 。这样的时间复杂度,相对于暴力枚举的 的时间复杂度就优秀得很多了。
例题
本题目列表会持续更新。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】