激活函数——sigmoid函数(理解)
0 - 定义
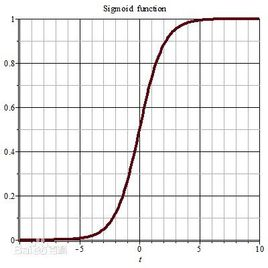
$Sigmoid$函数是一个在生物学中常见的S型函数,也称为$S$型生长曲线。在信息科学中,由于其单增以及反函数单增等性质,$Sigmoid$函数常被用作神经网络的阈值函数,将变量映射到0,1之间。
其曲线如下图:
1 - 导数
$$\begin{align*}
sigmoid^{'}(x)&=(\frac{1}{1+e^{-x}})^{'} \\
&=\frac{1}{1+e^{-x}}e^{-x}(-1)\\
&=\frac{e^{-x}}{(1+e^{-x})^2}\\
&=\frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}})\\
&=sigmoid(x)(1-sigmoid(x))
\end{align*}$$
2 - 参考资料
https://baike.baidu.com/item/Sigmoid函数/7981407?fr=aladdin



 浙公网安备 33010602011771号
浙公网安备 33010602011771号