CircleNet: Anchor-Free Glomerulus Detection withCircle Representation(理解)
扫码关注下方公众号:"Python编程与深度学习",领取配套学习资源,并有不定时深度学习相关文章及代码分享。

今天分享一篇发表在MICCAI 2020上的论文:CircleNet: Anchor-Free Glomerulus Detection with Circle Representation (原文链接:[1],github:[2])。
1 研究背景
目标检测分享中,anchor-based方法(Faster-RCNN等)通常会产生较高的模型复杂度和较低的灵活性,因为每一个位置需要采用多个anchor进行表达以及优化。因此最近有越来越多的anchor-free检测方法涌现,它们具有更简单的网络设计、更少的超参数却可能具有更好的性能。但是直接采用自然场景下的目标检测算法运用到病例图像的目标检测上可能不太适用,例如下图(Fig.1),对于肾小球的检测,如果采用bounding box框住目标,单病理图像旋转的时候,对应的bounding box形状也会变化,而如果采用bounding circle来框住目标,就可以确保检测对象的旋转不变性。
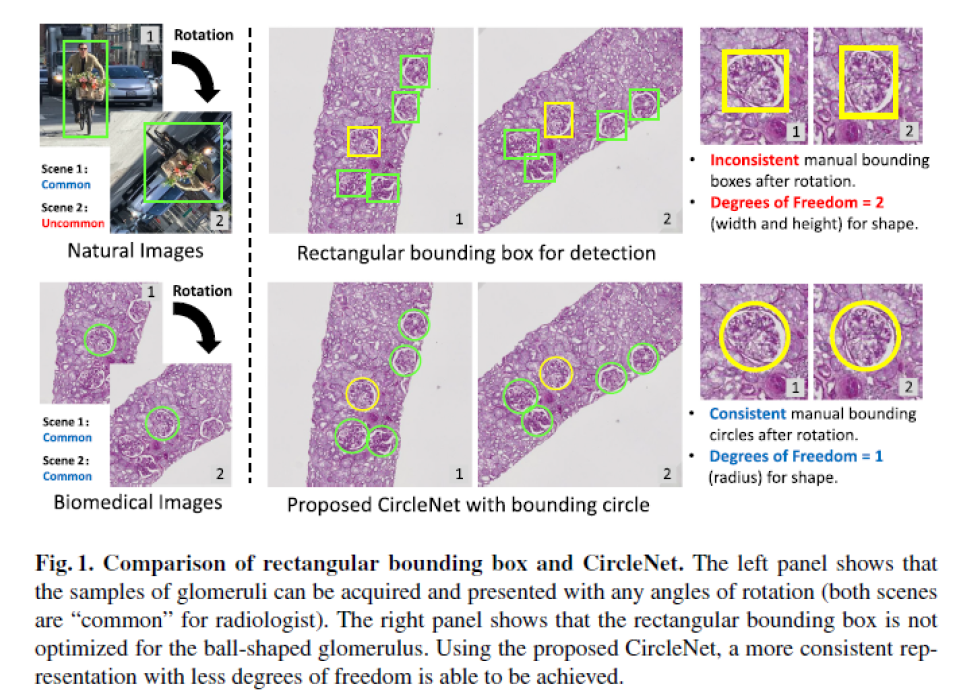
有了上述的这个分析,网络可以大大简化,从学习bounding box转变成学习bounding circle的表达。因此,文中提出了一种基于circle表达的anchor-free目标检测算法,叫做CircleNet,以用来检测肾小球。
这篇文章有如下几点贡献:
- 优化了病例目标检测算法:第一个采用基于circle的anchor-free方法进行肾小球的目标检测;
- circle表达:提出用bounding circle来框住物体,使得模型只用学习半径这一个维度(bounding box需要学习长和高两个维度),并且定义了cIOU (circle intersection over union)来衡量检测的性能;
- 旋转一致性:CircleNet在肾小球任务上实现了更好的旋转一致性。
2 方法
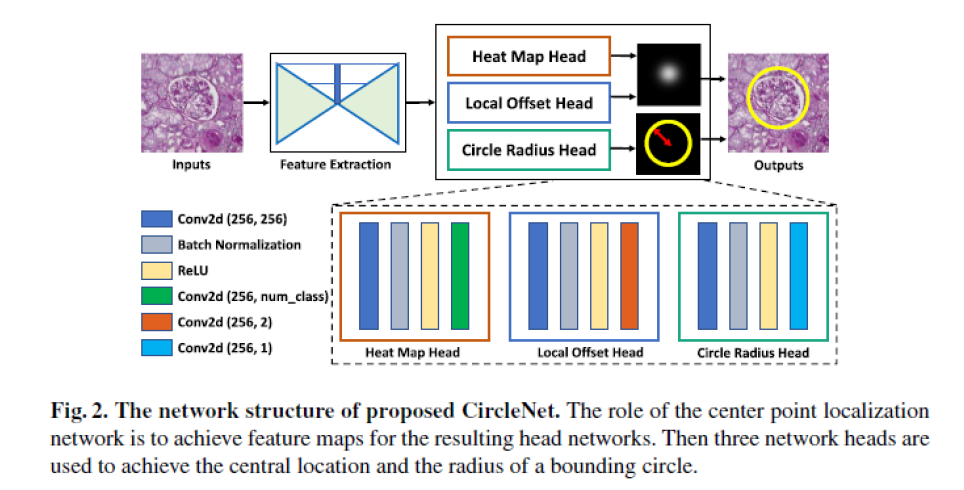
如上图(Fig.2)所示,整体流程为:通过特征提取网络提取图像的特征,而后分别采用三个输出模块预测(1)heatmap,用来表示circle的中心点;(2)local offset,用来修正circle的中心点位置;(3)circle radius:用来表达circle的半径。
2.1 Anchor Free骨干网络
骨干网络是基于CenterNet的实现。假设输入图像$I$的维度为$I\in R^{W\times H\times 3}$,则heatmap的维度为$\hat{Y}\in [0,1]^{\frac{W}{R}\times \frac{H}{R}\times C}$,$C$表示待识别的类别数,$R$表示模型的下采样率。目标中心点的标签由2D的高斯核描述:
$$Y_{xyc}=exp\left (-\frac{(x-\tilde{p}_x)^2+(y-\tilde{p}_y)^2}{2\sigma_p^2}\right ),$$
其中$\tilde{p}_x$和$\tilde{p}_y$是目标中心点经过下采样之后的位置,$\sigma_p$是高斯核的标准差,预测的heatmap采用像素级别的focal loss进行优化:
$$L_k=\frac{-1}{N}\sum_{xyc}\left\{\begin{matrix}(1-\hat{Y}_{xyc})^{\alpha}log(\hat{Y}_{xyc})\ if\ Y_{xyc}=1\\(1-Y_{xyc})^{\beta}(\hat{Y}_{xyc})^{\alpha}\ otherwise\\log(1-\hat{Y}_{xyc}))\ otherwise\end{matrix}\right.$$
其中$\alpha$和$\beta$是focal loss的超参数。
而后使用$\mathcal l_1-norm$偏移预测损失$L_{off}$来修正预测坐标,这部分和CenterNet中一致。
2.2 从中心点到Bounding Circle
一旦heatmap被预测出来,只需要取heatmap中前$n$个峰值就可以表示$n$个检测对象的中心点,定义为$\hat{\mathcal P}=\{(\hat{x}_i,\hat{y}_i)\}_{i=1}^n$。而后通过解析$\hat{Y}_{x,y,c}$和$L_k$便可以得到中心点的精确坐标:
$$\hat{p}=(\hat{x}_i+\delta\hat{x}_i,\hat{y}_i+\delta\hat{y}_i),$$
然后在半径预测图$\hat{R}\in\mathcal R^{\frac{W}{R}\times\frac{H}{R}\times 1}$中找到对应位置的值就可以得到该中心点对应的半径:
$$\hat{r}=\hat{R}_{\hat{x}_i,\hat{y}_i},$$
预测半径的损失计算:
$$L_{radius}=\frac{1}{N}\sum_{k=1}^N\left | \hat{R}_{p_k}-r_k\right |,$$
综上,对于第$k$个circle目标的损失函数可以表示为:
$$L_{det}=L_k+\lambda_{radius}L_{radius}+\lambda_{off}L_{off},$$
文中将上述超参设置为$\lambda_{radius}=0.1$和$\lambda_{off}=1$。
2.3 Circle IOU
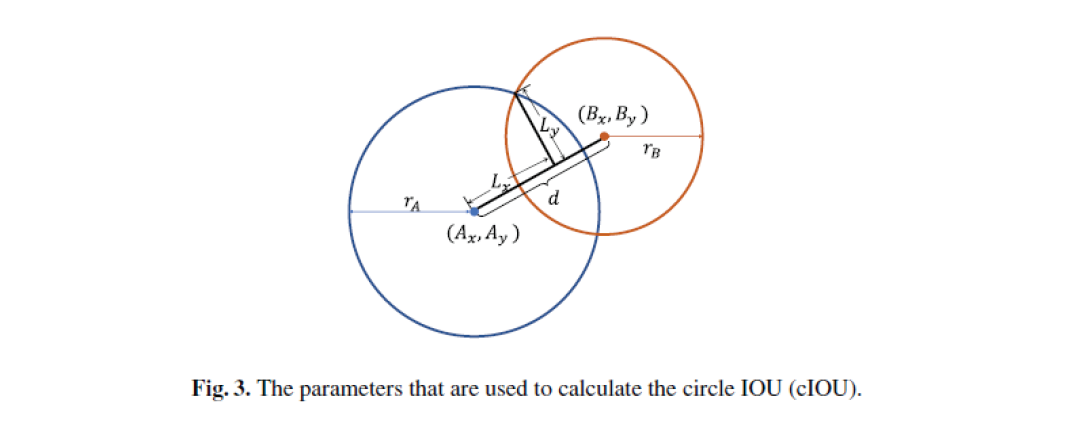
如上图(Fig.3)所示,类似IOU的计算,文中把cIOU定义为:
$$cIOU=\frac{Area(A\cap B)}{Area(A\cup B)},$$
其中$A$和$B$分别表示两个cicles。将它们的中心点表示为$(A_x,A_y)$和$(B_x,B_y)$,如下:
$$A_x=\hat{x}_i+\delta\hat{x}_i,A_y=\hat{y}_i+\delta\hat{y}_i$$
$$B_x=\hat{x}_j+\delta\hat{x}_j,B_y=\hat{y}_j+\delta\hat{y}_j$$
那么两个中心点之间的距离可以定义为:
$$d=\sqrt{(B_x-A_x)^2+(B_y-A_y)^2}$$
$$L_x=\frac{r_A^2-r_B^2+d^2}{2d},L_y=\sqrt{r_A^2-L_x^2}$$
最终cIOU可以通过如下公式计算:
$$Area(A\cap B)=r^2_A sin^{-1}\left (\frac{L_y}{r_A}\right )+r^2_B sin^{-1}\left (\frac{L_y}{r_B}\right )-L_y\left (L_x+\sqrt{r_A^2-r_B^2+L_x^2}\right )$$
$$Area(A\cup B)=\pi r_A^2+\pi r_B^2-Area(A\cap B)$$
3 实验结果
这里我只给出论文中的部分实验结果,具体的实验结果分析以及实验和参数的设置请看原文。
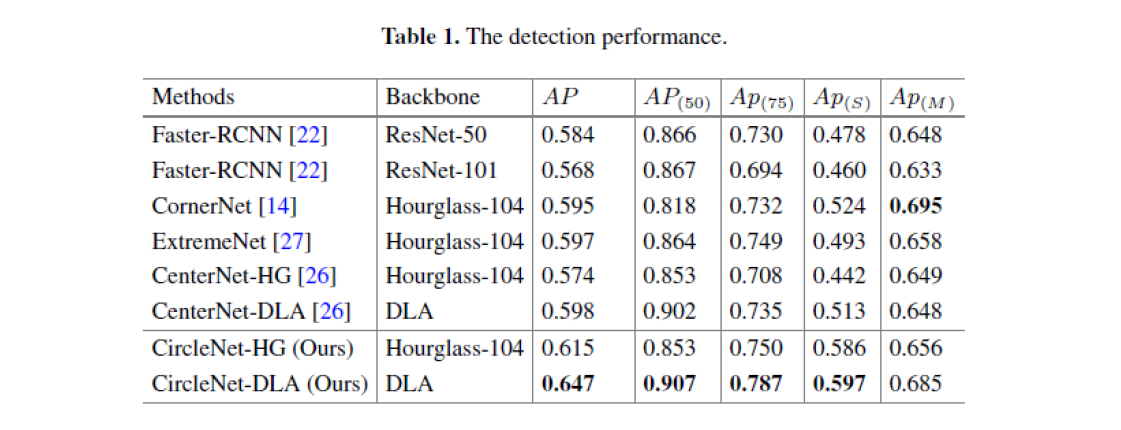

4 参考资料
[1] https://link.springer.com/chapter/10.1007/978-3-030-59719-1_4
[2] https://github.com/hrlblab/CircleNet


 浙公网安备 33010602011771号
浙公网安备 33010602011771号