BBN: Bilateral-Branch Network with Cumulative Learning for Long-Tailed Visual Recognition(理解)
扫码关注下方公众号:"Python编程与深度学习",领取配套学习资源,并有不定时深度学习相关文章及代码分享。

今天分享一篇发表在CVPR 2020上的论文:BBN: Bilateral-Branch Network with Cumulative Learning for Long-Tailed Visual Recognition (原文链接:[1])。
1 研究背景
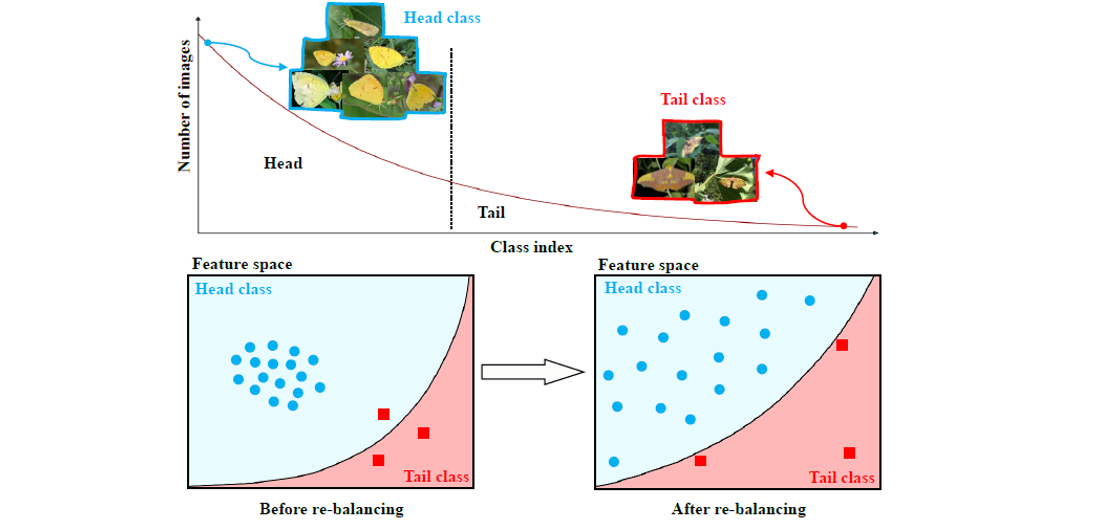
如上图所示,计算机视觉识别任务中经常面临长尾数据分布的挑战,即少数类占有多数样本,多数类只有少数样本。解决这个问题主要有两类方法:重采样(Re-Sampling, RS)和重新分配损失权重 (Re-Weighting, RW)。具体地,重采样可以对少数样本类进行过采样或者对多数样本类进行降采样,还可以通过一些合成方法合成新的样本,其目的是通过采样方法使得类间样本数分布趋于平衡。重新分配权重是根据不同类别的不同样本数决定其损失值的惩罚系数大小,比如对于少数样本类,其损失惩罚应该更大,通常的做法是为交叉熵损失加上各个类别的权重系数,该系数通常定义为类别样本数的倒数。

如上图(Figure 2)所示,这篇文章先将分类学习任务解耦成两部分:表征学习和分类器学习。并且通过对比实验讨论分析了RW和RS分别对于表征学习和分类器学习的影响。如下图(Figure 2)所示,以左边图为例,先看第1列,即固定表征学习部分的参数(采用交叉熵CE训练得到的),从上往下3行分别表示采用RS、RW、CE训练得到的分类器,其中RS得到的模型效果最好,RS和RW有利于分类器的学习。再看第1行,即固定分类器部分的参数(采用RS训练得到的),从左往右分别是采用CE、RW、RS训练的表征学习部分,可以看到CE反而是性能最好的,RW和RS实际上会对表征学习产生一些负面影响。其它行和列分析同上。因此文中认为,表征学习部分应该在数据原有的分布上进行训练,RS和RW这些改进方法只需要加在分类器学习上即可,从而提出了Bilateral-Branch Network (BBN)以提高模型在长尾分布数据上的性能。
2 方法
2.1 整体流程

如上图(Figure 3)所示,文中提出的BBN框架包含了三个主要部分:卷积学习分支(conventional learning branch)、重平衡分支(re-balancing branch)和累计学习策略(cumulative learning)。其中卷积学习分支和重平衡分支共享网络参数(除了最后一个residual block)。假设一对训练样本描述为$x,y\in\{1,2,\cdots,C\}$,其中$C$表示类别的数量。卷积学习分支和重平衡分支分别采用均匀采样和逆采样(具体可见下一节分析),采样的样本分别表示为$(x_c, y_c)$和$(x_r,y_r)$,两类样本分别喂入各自的分支产生特征向量$\mathbf{f}_c\in\mathbb{R}^D$和$\mathbf{f}_r\in\mathbb{R}^D$。而后通过累计学习策略综合两个分支的输出。具体地,定义权衡参数$\alpha$,将$\alpha\mathbf{f}_c$和$(1-\alpha)\mathbf{f}_r$分别作为分类器$\mathbf{W}_c\in\mathbb{R}^{D\times C}$和$\mathbf{W}_r\in\mathbb{R}^{D\times C}$的输入,而后两个分类器的输出做元素相加,这个过程可以用如下公式表示,
$$\mathbf{z}=\alpha\mathbf{W}_c^T\mathbf{f}_c+(1-\alpha)\mathbf{W}_r^T\mathbf{f}_r,$$
其中$\mathbf{z}\in\mathbb{R}^C$为对每个类别的预测,例如对于每一个类别$i\in\{1,2,\cdots,C\}$的预测表示为$\left [z_1,z_2,\cdots,z_C\right ]^T$,再通过softmax函数可以得到每一个类别的预测概率,
$$\hat{p}_i=\frac{e^{z_i}}{\sum_{j=1}^Ce^{z_j}},$$
然后通过交叉熵损失函数$E(\cdot,\cdot)$计算对于预测概率$\hat{\mathbf{p}}=\left [\hat{p}_1,\hat{p}_2,\cdots,\hat{p}_C\right ]^T$的损失值。最终的损失函数可以表示为,
$$\mathcal{L}=\alpha E(\hat{\mathbf{p}},y_c)+(1-\alpha)E(\hat{\mathbf{p}},y_r).$$
2.2 卷积学习分支和重平衡分支
2.2.1 数据采样
上一节提到卷积学习分支和重平衡分支的输入分别采用均匀采样和逆采样。其中均匀采样是指对于每一个样本在每一个epoch中都有等概率被采样一次,这种采样方法能够反映数据的原始分布,因此有利于表征学习。逆采样中将每个类的抽样概率设置为与其样本数量的倒数成正比,类别中样本数越多,采样概率越小,假设第$i$个类别的样本数为$N_i$,最多的类别样本数为$N_{max}$,那么逆采样过程分为以下三步:
1. 计算第$i$个类别的采样概率$P_i=\frac{w_i}{\sum_{j=1}^C w_j},w_i=\frac{N_{max}}{N_i}$
2. 按照概率$P_i$选择一个类别
3. 从该类别中等概率选择一个样本
重复上述过程即可得到一个mini-batch的数据。
2.2.2 权重共享
文中采用ResNets(ResNet-32和ResNet-50)作为骨干网络,卷积学习分支和重平衡分支共享除了最后一个residual block的骨干网络。文中认为两个分支共享权重具有两个优势:
1. 卷积学习分支学习到的好的表征能够帮助重平衡分支更好的学习
2. 共享特征能够在推理时大量地减少计算复杂度
2.3 累积学习策略
提出累计学习策略是为了权衡卷积学习分支和重平衡分支对于最后分类损失$\mathcal{L}$的贡献程度。其设计目的是先学习通用的特征表达模式,而后逐渐关注尾部数据。上述的过程通过控制2.1节提到的$\alpha$权衡参数实现,该参数定义为,
$$\alpha=1-\left (\frac{T}{T_{max}}\right )^2,$$
$\alpha$随着训练的进行越来越小,即一开始更加关注卷积学习分支中的表征学习,而后慢慢将注意力放在重平衡分支的分类器学习上。
2.4 推理过程
在推理过程中,测试样本将同时作为卷积学习分支和重平衡分支的输入,分别产生输出$\mathbf{f}_c'$和$\mathbf{f}_r'$,并且固定$\alpha$为0.5,以保证两个分支是同等重要的。而后两个输出分别送入相应的分类器$\mathbf{W}_c$和$\mathbf{W}_r$产生两个概率预测,将这两个概率预测逐元素相加得到最终分类器的输出。
3 实验结果
这里我只给出论文中的部分实验结果,具体的实验结果分析以及实验和参数的设置请看原文。
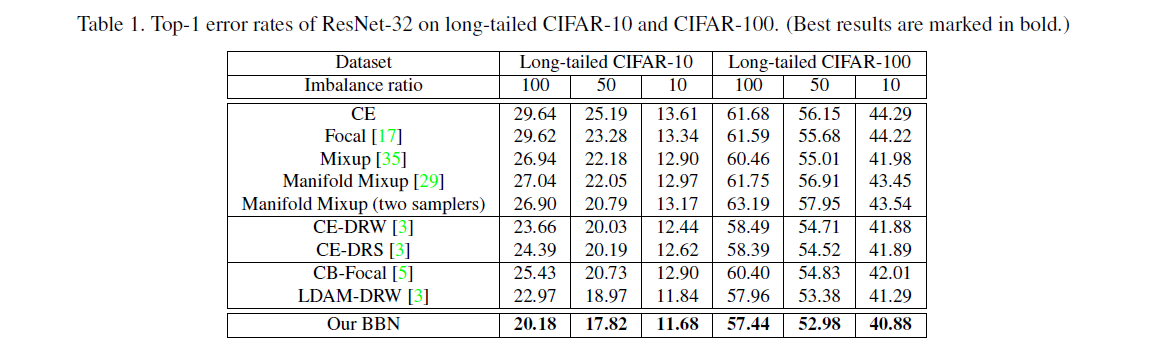
4 参考资料
[1] https://arxiv.org/abs/1912.02413


 浙公网安备 33010602011771号
浙公网安备 33010602011771号