Label Transfer by Learning Reversible Voxel-wise Correspondence for One-shot Medical Image Segmentation(理解)
扫码关注下方公众号:"Python编程与深度学习",领取配套学习资源,并有不定时深度学习相关文章及代码分享。

今天分享一篇发表在CVPR 2020上的论文:LT-Net: Label Transfer by Learning Reversible Voxel-wise Correspondence for One-shot Medical Image Segmentation (原文链接:[1])。
1 研究背景
近年来随着深度学习的快速发展,深度卷积神经网络 (DCNNs)在许多分割任务上取得很好的性能。但是对于3D医学图像分割任务,获得3D空间中的体素标注是困难的,因此模型需要学习如何从一个或者少量几个标注样本中进行有效地学习。
对于这个问题,传统的解决方案是atlas-based的分割方法。而在这篇文章中,作者直接采用深度学习模型来模拟atlas-based的经典分割方法,提出了LT-Net。LT-Net以atlas有标注图像和无标注图像作为输入,预测前者到后者的对应映射关系,这样子就可以利用映射关系将atlas图像上的分割图转移到无标注的图像上。
这篇文章主要有三点贡献:
- 为了解决缺少标注的问题,借助经典的atlas-based方法的分割思想来解决one-shot分割问题
- 以端到端方式将对应映射关系的学习扩展到one-shot分割框架中,其中前向和反向构成的循环一致性 (forward-backward cycle-consistency)在图像、转换和标签空间中起到了额外监督的重要作用 (注:这里的前向和反向不同于深度学习的前向传播和反向传播,具体见后面章节的描述)
- 通过充分的实验证明所提出方法的有效性
2 方法
2.1 整体流程
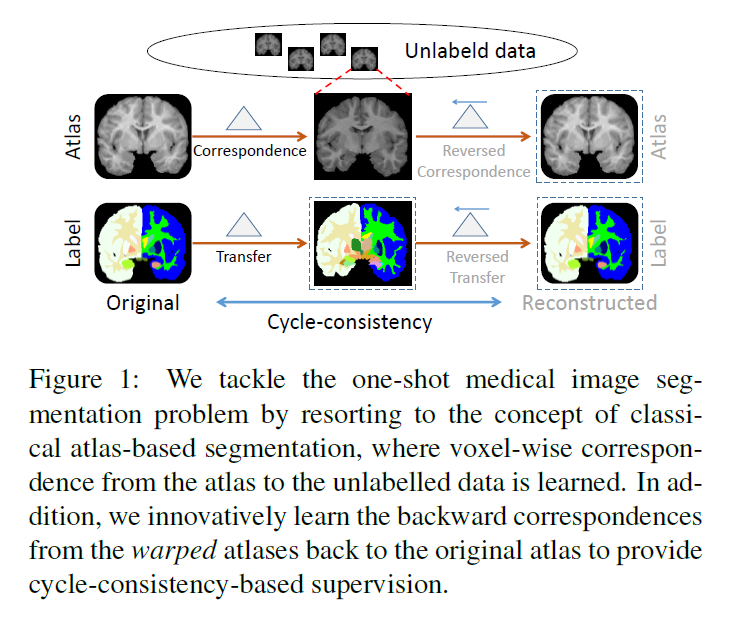
假设$(l,l_s)$表示一对具有标注的图像对,其中$l\in \mathbb{R}^{h\times w\times c}$是atlas图像,$l_s\in \mathbb{R}^{h\times w\times c}$是对应的分割图。对于所有输入图像,他们都被定义在3D空间$\Omega\in\mathbb{R}^3$中,其中无标注图像集合可以表示为$\{u^{(i)}|u^{(i)}\in\mathbb{R}^{h\times w\times c}\}$,后面将采用$u$来表示一副无标注的图像。
在这篇文章中,作者希望模型不单单能够学习从$l$到$u$的对应映射关系,也应该学习从$u$到$l$的对应映射关系,对于前者称为前向过程 (forward),对于后者称为反向过程 (backward)。
首先采用$\Delta_{p_F}$表示有标注的atlas图像$l$和无标注图像$u$之间的对应映射关系(前向过程),则将$\Delta_{p_F}$作用在$l$上的过程可以表示为:
$$\bar{u}=l\circ\Delta_{p_F},$$
其中$\circ$表示变换操作 (warp operation),$\bar{u}$表示从$l$变换出来的atlas图像,那么其对应的分割图可以由$l_s$经过同样的映射关系变换得到:
$$\bar{u}_s=l_s\circ\Delta_{p_F},$$
然后采用$\Delta_{p_B}$表示无标注图像$u$到有标注的atlas图像$l$之间的对应映射关系(反向过程),则将$\Delta_{p_B}$作用在$\bar{u}$上的过程可以表示为:
$$\bar{l}=\bar{u}\circ\Delta_{p_B},$$
对应的分割图也可以进行变换:
$$\bar{l}_s=\bar{u}_s\circ\Delta_{p_B},$$
其中我们期望$\bar{l}$以及$\bar{l}_s$应该分别和$l$以及$l_s$是一致的,因此上述的这两个过程就构成了一个循环 (cycle)。接下来的两小节将详解怎么构造模型来对$\Delta_{p_F}$和$\Delta_{p_F}$进行预测。

2.2 前向对应映射关系的学习
文中采用DCNN(例如VoxelMorph)构成的生成网络$G_F$来学习对应的映射关系$\Delta_{p_F}$,其输入是$l$和$u$,输出是他们之间的对应关系$\Delta_{p_F}$,网络的优化过程是通过最小化两个无监督损失函数:
- 图像相似度损失函数$\mathcal{L}_{sim}(u,\bar{u})$:采用局部归一化互相关损失 (locally normalized cross-correlation (CC) loss)
- 转换平滑损失函数$\mathcal{L}_{smooth}(\Delta_{p_F})=\sum_{t\in\Omega}\left\|\bigtriangledown(\Delta_{p_F}(t))\right\|_2$
除了上述两个损失函数之外,文中还加入了辅助GAN损失方式来提供额外的监督。GAN子网络由$G_F$和判别器$D$构成,目的是使得通过$G_F$生成的$\bar{u}$能够在判别器$D$下“蒙混过关”。这部分的损失函数定义为:
$$\mathcal{L}_{GAN}(l,u,\bar{u})=\mathbb{E}_{u\sim p_d(u)}[\left\|D(u)\right\|]_2+\mathbb{E}_{l\sim p_d(l),u\sim p_d(u)}[\left\|D(\bar{u})-\mathbf{1}\right\|_2],$$
其中$G_F$和$D$在目标函数下交替训练,在两者的最小-最大博弈中进行学习:$$min_{G_F}max_D\mathcal{L}_{GAN}(G_F,D).$$
2.3 反向对应映射关系的学习
文中把上述2.1小节中介绍的反向过程中的对应映射关系$\Delta_{p_B}$称为反向对应映射关系,同样采用DCNN(例如VoxelMorph)构成的生成网络$G_B$来进行学习,有$\Delta_{p_B}=G_B(\bar{u},l)$。因此对于上面2.2小节中由$G_F$生成的$\bar{u}$,可以再通过$G_B$生成$l$的重构atlas图像$\bar{l}$,表示如下:
$$\bar{l}=\bar{u}\circ\Delta_{p_B},$$
结合上面2.2小节,总的转换平滑损失函数可以表示为:
$$\mathcal{L}_{smooth}=\mathcal{L}_{smooth}(\Delta_{p_F})+\mathcal{L}_{smooth}(\Delta_{p_B}),$$
此外,如Figure 2所示,$G_F$和$G_B$构成的循环中可以加入三个监督信号:
- 图像空间上的循环一致性监督:$l$根据$G_F$的预测结果转换成$\bar{u}$,$\bar{u}$再根据$G_B$的预测结果转换为$\bar{l}$,其中期望$\bar{l}$与$l$是一致的,因此加入L1损失函数进行监督学习,有:$$\mathcal{L}_{cyc}(l,\bar{l})=\mathbb{E}_{l\sim p_d(l)}[\left\|\bar{l}-l\right\|_1],$$
- 转换空间上的循环一致性监督:对于某个位置,通过前向过程转换之后,再通过反向过程的转换应该回到原来的位置,这部分的损失可以表示为:$$\mathcal{L}_{trans}(\Delta_{p_F},\Delta_{p_B})=\sum_{t\in \Omega}\rho(\Delta_{p_F}(t)+\Delta_{p_B}(t+\Delta_{p_F}(t))),\rho(x)=(x^2+\epsilon^2)^{\gamma},$$
- 标签空间上的循环一致性监督(第一部分):$l_s$根据$G_F$的预测结果转换成$\bar{u}_s$,$\bar{u}_s$再根据$G_B$的预测结果转换为$\bar{l}_s$,其中期望$\bar{l}_s$与$l$是一致的,加入Dice损失函数进行监督,有:$$\mathcal{L}_{anatomy\_cyc}(l_s,\bar{l}_s)=1-\frac{2\sum_{t\in\Omega}l_s(t)\bar{l}_s(t)}{\sum_{t\in\Omega}l_s^2(t)+\sum_{t\in\Omega}\bar{l}_s^2(t)},$$
- 标签空间上的循环一致性监督(第二部分):由于模型的目标是学习可用于将altas图像上的分割图转移到每个未标注图像的对应关系,因此文中还额外提出了差异一致性损失,以间接地规范化合成的分割图的质量,有:$$\mathcal{L}_{diff\_cyc}(l_s,\bar{u}_s,\bar{l}_s)=\sum_{t\in\Omega}\rho(\left |l_s(t)-\bar{u}_s(t)\right |-\left |\bar{u}_s(t)-\bar{l}_s(t)\right |).$$
2.4 损失函数
综合上述2.2小节和2.3小节,整个模型的优化目标可以表示为:
$$\mathcal{L}=\mathcal{L}_{GAN}+\mathcal{L}_{sim}+\lambda_1\mathcal{L}_{cyc}+\lambda_2(\mathcal{L}_{anatomy\_cyc}+\mathcal{L}_{smooth}+\mathcal{L}_{trans}+\mathcal{L}_{diff\_cyc}),$$
其中$\lambda_1=10,\lambda_2=3.$
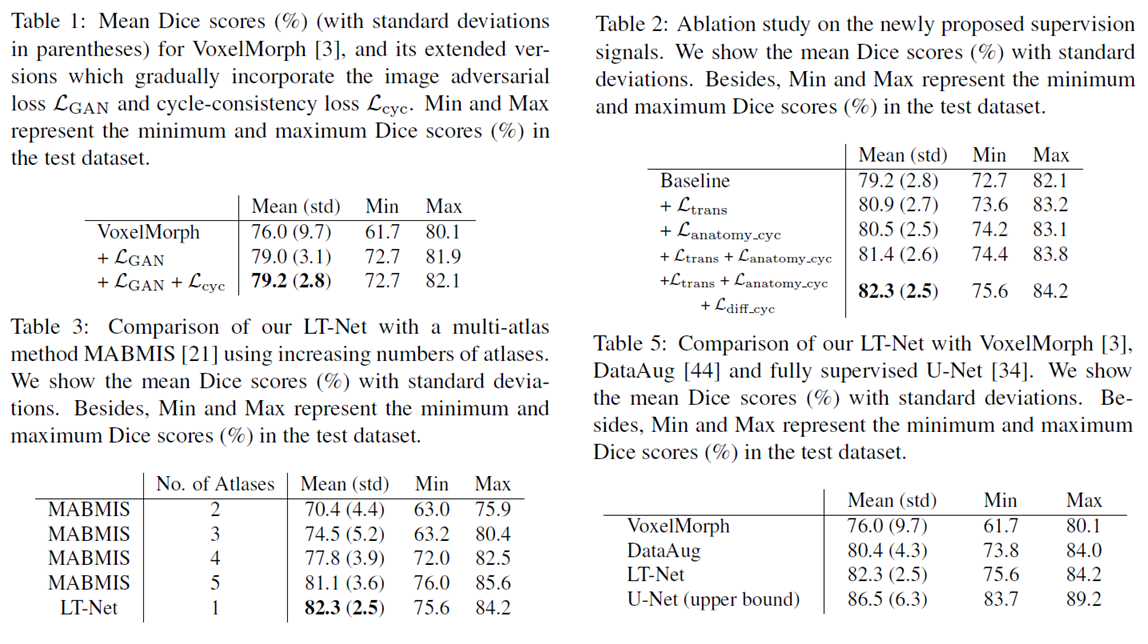
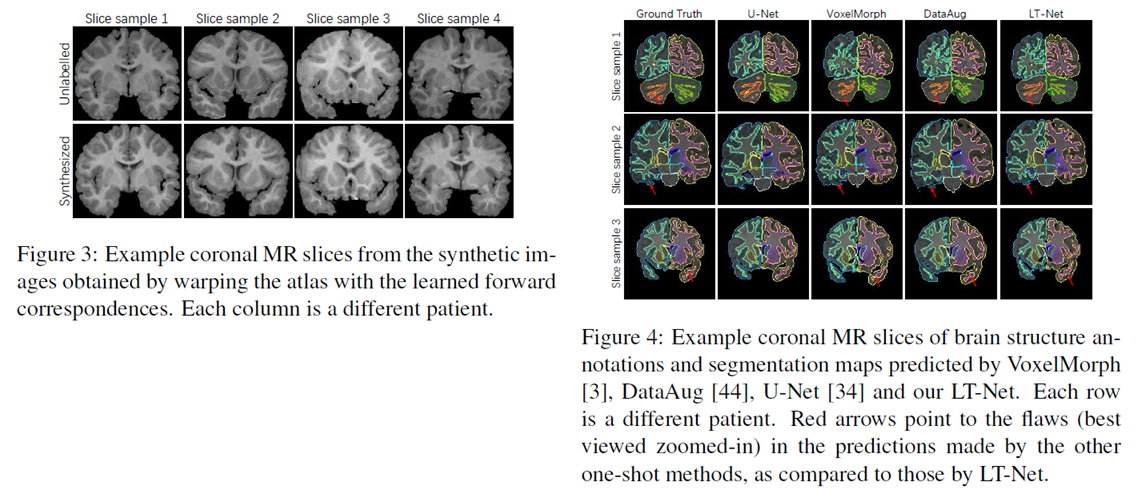
3 实验结果
这里我只给出论文中的部分实验结果,具体的实验结果分析以及实验和参数的设置请看原文。

4 参考资料
[1] http://openaccess.thecvf.com/content_CVPR_2020/papers/Wang_LT-Net_Label_Transfer_by_Learning_Reversible_Voxel-Wise_Correspondence_for_One-Shot_CVPR_2020_paper.pdf




