Uncertainty-aware Self-ensembling Model for Semi-supervised 3D Left Atrium Segmentation(理解)
扫码关注下方公众号:"Python编程与深度学习",领取配套学习资源,并有不定时深度学习相关文章及代码分享。

今天分享一篇发表在MICCAI 2019上的论文:Uncertainty-aware Self-ensembling Model for Semi-supervised 3D Left Atrium Segmentation (原文链接:[1],代码链接:[2])。
1 研究背景
训练深度卷积神经网络通常需要大量的标签数据,然而对于医学影像分割任务,大量数据的标注成本很高,因此考虑怎么同时利用好仅有的标签数据和无标签数据(半监督方法)在医学影像处理中是非常重要的。这篇文章针对3D MR图像的左心房分割任务提出了不确定性感知自增强模型,能够更有效地利用无标签数据从而获得更好的性能。
2 方法
2.1 整体流程
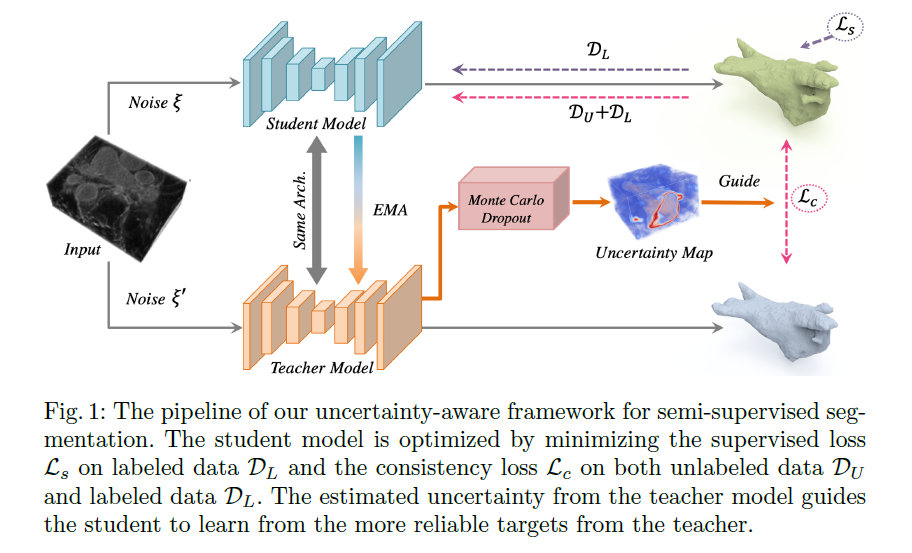
如上图(Fig.1)所示,对于有标签数据,学生模型 (student model)进行有监督学习。对于无标签数据,通过教师模型 (teacher model)预测分割图,作为学生模型 (student model)的学习目标,并同时评估学习目标的不确定性。基于学习目标的不确定性,采用一致性损失函数提高学生模型的性能。
2.2 半监督分割 (Semi-supervised segmentation)
对于3D数据的半监督任务,假设有$N$个标签数据和$M$个无标签数据,那么有标签数据集可以表示为$\mathcal{D}_L=\{(x_i,y_i)\}_{i=1}^N$,无标签数据集可以表示为$\mathcal{D}_U=\{(x_i)\}_{i=N+1}^{N+M}$,其中$x_i\in\mathbb{R}^{H\times W\times D}$是输入数据,$y_i\in \{0,1\}^{H\times W\times D}$是标签数据。文中的半监督分割框架的学习目标为:
$$\min_{\theta}\sum_{i=1}^{N}\mathcal{L}_s(f(x_i;\theta))+\lambda\sum_{i=1}^{N+M}\mathcal{L}_c(f(x_i;\theta',\xi'),f(x_i;\theta,\xi))$$
其中$\mathcal{L}_s$为在有标签数据上计算的有监督损失部分(交叉熵损失),$\mathcal{L}_c$为在无标签数据上计算的教师模型和学生模型之间的无监督损失部分。$f(\cdot)$表示分割神经网络,$(\theta',\xi')$和$(\theta,\xi)$分别表示教师模型和学生模型中的参数和的不同扰动(例如给输入加入噪声或者网络中加入dropout)。$\lambda$是控制有监督损失部分和无监督损失部分的权衡参数。
此外,[9][14]中证明了集成网络在不同训练阶段的预测结果能够有效地提高预测结果,因此文中采用了指数移动平均 (exponential moving average, EMA)策略来提高教师模型的预测结果。具体地,教师模型的参数$\theta'$的更新策略为:
$$\theta_t'=\alpha\theta_{t-1}'+(1-\alpha)\theta_t$$
其中$\theta_t$是学生模型在第$t$次训练迭代中的参数,$\alpha$是用来控制EMA更新速度的参数。
2.3 不确定性感知 (Uncertainty-Aware Mean Teacher Framework)
教师模型对于无标签数据的预测结果是不确定性且有噪声的,而这些预测结果将作为学生模型学习的一部分 ($\mathcal{L}_c$),因此作者设计了不确定性感知策略使得学生模型能够逐渐学习更加可靠的目标。具体地,对于训练图像,教师模型不仅要预测它们的分割图,还要评估它们的不确定性。然后学生模型在学习中只选取其中具有更低的不确定性(更加可靠)的数据计算一致性损失 (consistency loss)。
2.3.1 不确定性评估 (Uncertainty Estimation)
不确定评估是由教师模型生成的,具体有:
1. 对于每一个输入数据,进行$T$次前向传播获得预测结果,每一次都随机对输入数据加入高斯噪声或者在网络中加入随机dropout。因此每一个体素都有$T$个预测结果,可以表示为$\{\mathbf{p}_t\}_{t=1}^T$
2. 采用预测熵 (predictive entropy)大致近似不确定性,具体有:$\mu_c=\frac{1}{T}\sum_t\mathbf{p}^c_t$,$u=-\sum_{c}\mu_clog\mu_c$,其中$\mathbf{p}_t^c$是对在第$t$次前向传播中对属于第$c$类别概率的预测。最终可以构成一个不确定性张量$U,\{u\}\in\mathbb{R}^{H\times W\times D}$
2.3.2 基于不确定性的一致性损失函数 (Uncertainty-Aware Consistency Loss)
有了上一步的教师模型预测的不确定性结果$U$,可以过滤掉相对不确定的预测,而选取相对可靠的预测作为学生模型的学习目标。具体如下:
$$\mathcal{L}_c(f',f)=\frac{\sum_v\mathbb{I}(u_v<{H})\left \|f_v'-f_v\right \|^2}{\sum_v\mathbb{I}(u_v<{H})}$$
其中$\mathbb{I}$是指示函数,如果条件成立则返回1,否则返回0,用以筛选出可靠的样本。$f_v'$和$f_v$分别是教师网络和学生网络在第$v$个体素位置的预测结果。$u_v$是不确定性张量$U$在第$v$个体素上的值,$H$是过滤不确定预测的阈值。作者提到,加入了基于不确定性的一致性损失函数,能够同时提高教师模型和学生模型的性能。
3 实验结果
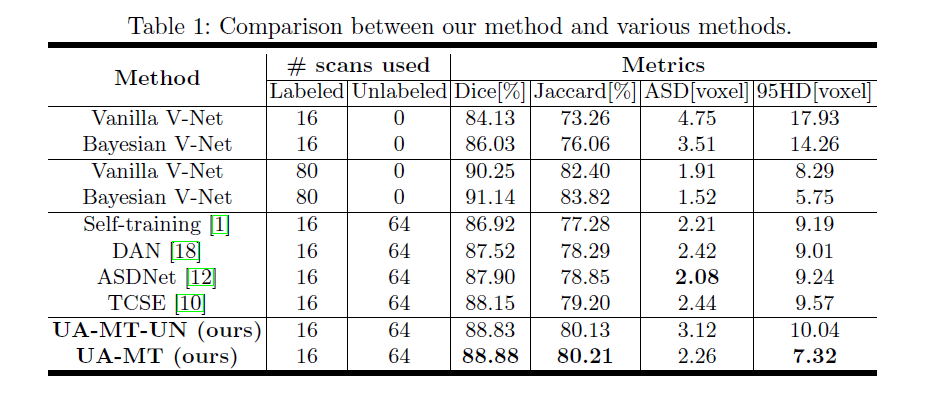
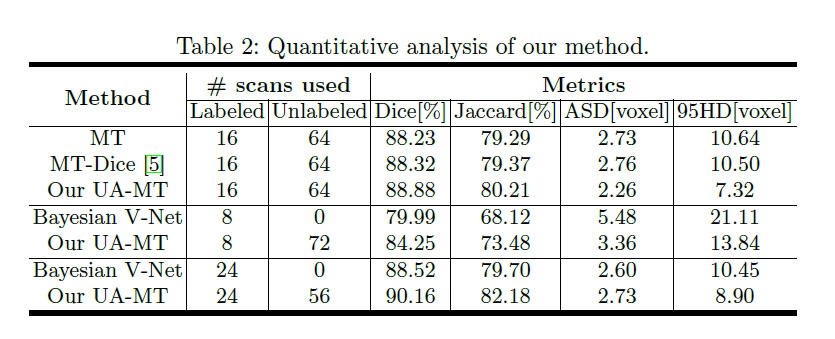
这里我只给出论文中的部分实验结果,具体的实验结果分析以及实验和参数的设置请看原文。

4 参考资料
[1] https://arxiv.org/pdf/1907.07034
[2] https://github.com/yulequan/UA-MT
[3] Laine, S., Aila, T.: Temporal ensembling for semi-supervised learning. arXiv preprint (2016)
[4] Tarvainen, A., Valpola, H.: Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. In: NIPS (2017)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号