Deep Gamblers: Learning to Abstain with Portfolio Theory（理解）（github代码）
（代码托管在我的Github上，如果有帮助记得点星星嗨！）
0 - 概要
选择分类问题(selective classification problem)是一类带有拒绝选项的监督学习问题，可以在一定程度的数据覆盖范围内获得最佳性能。文中将原始的m分类问题转化成(m+1)分类问题，其中第(m+1)表示模型由于置信度不够而放弃预测。受最佳证券投资理论(portfolio theory)的启发，文中基于博弈翻倍率(doubling rate of gambling)的损失函数来解决选择分类问题。最小化这个损失函数自然对应于将一场赛马的收益最大化，在这种情况下，博弈者的目标是在对结果下注(做出预测)和不确定的情况下保留奖金(放弃预测)之间取得平衡。这个损失函数允许以端到端方式来训练网络以及描述预测的不可靠性。与之前的方法相比，文中的方法几乎不需要修改模型推理算法或者模型结构。实验结构表明我们的方法能够较好地识别数据点的不确定性，并能在SVHN、CIFAR10以及Cat vs. Dog三个经典分类数据集上的不同覆盖规模上获得好结果。但获得样本的不确定性之后，文中没有进一步对不确定样本的学习进行挖掘，因此我提出了一种改进策略，称为基于动态分配的在线硬样本挖掘策略，在训练过程中挖掘硬样本使得分类器能够获得更好的性能，同时这种策略理论上可以很容易应用于所有深度学习中的有监督学习任务上。论文实验的复现以及改进的代码我已经开源在github上。
1 - 选择预测问题
假设$X$表示图片的分布，$Y$表示标签类别的分布，我们的目标是学习条件分布$P(Y|X)$和一个以权值$w$为参数的预测模型$f_w:X\rightarrow Y.$那么数据集可以表示为$\left\{(x_i,y_i)\right\}_{i=1}^N$，其中$(x_i,y_i)$是从$X\times Y$中独立抽样的。扩充了拒绝选项的预测模型是一对函数$(f,g)$，其中$g_h:X\rightarrow \mathbb{R}$是一个选择函数，其可以解释为$f$的二分限定词(binary qualifier)如下，
即当选择函数$g(x)$低于预定的阈值$h$的时候，模型放弃预测。我们称$g(x)$为$x$的不确定分数；不同的模型趋向于使用不同的$g(x)$。覆盖数据集(the covered dataset)定义为${x:g_h(x)\geq h}$，覆盖率是覆盖数据集的大小与原始数据集的大小之比。显然地，人们会为了更低的风险而权衡覆盖率，这就是拒绝选项方法背后的动机。
2 - 方法
这篇文章提出方法背后的直觉是，一个学习放弃预测的深度学习模型实际上是在模仿一个博弈者如何在游戏中保留赌注。实际上，我们对于一个m分类问题，我们可以通过一个m+1类的分类器来预测m个类别的概率以及一个额外的第(m+1)类作为拒绝分数。
2.0 - 最佳证券投资理论
该理论认为，如果我们有一些预算，我们应该在我们愿意押多少注和储蓄多少之间进行分配。为了保持术语的清晰，如表1所示，文中给出了最佳证券投资理论及在深度学习中相应的概念的对应关系。
简单来说，最佳证券投资理论告诉我们投资股票市场的最佳方式。假设股票市场中有m只股票，定义$price\ relaive\ X_i$为第i只股票在一天结束时的价格与一天开始时的价格之比，则m只股票可以表示为向量$\mathbf{X}=(X_1,\cdots,X_m)$，且满足从分布中抽样$\mathbf{X}\sim P(\mathbf{X})$。投资组合是指我们在股票市场的投资，可以通过一个离散分布$b=(b_1,\cdots,b_m),b_i\leq 0,\sum_i b_i=1$进行建模，该分布表示对应每只股票的投资比率。因此，一天结束时的财富可以表示为$S=b^TX=\sum_i b_iX_i$，其表示我们一天结束时的财富与我们这天开始时财富的比值。
定义1：股票市场投资组合$b$相对于股票分布$P(\mathbf{x})$的翻倍率表示为
$$W(b,P)=\int log_2(b^Tx)dP(x).$$
上述定义告诉我们我们财富的增长速度，因此我们期望去最大化$W$，下面只考虑简化版的最佳证券投资理论，称为“赛马”(horse race)问题。
2.1 - 赛马问题
不同于股票市场，赛马每一次只有一匹马赢得比赛，每匹马的只可能赢或者输，则假设第j匹马赢得比赛，可以用one-hot向量表示为表示为$x(j)=(0,\cdots,0,1,0,\cdots,0)$，其中第$j$个位置为1，其余为0。在赛马中，我们要在m匹马上进行押注，第i匹马赢得比赛的概率为$p_i$，若假设押注第i匹马并且第i匹马赢得比赛的回报为$o_i$，否则回报为0，并且假设押注者的押注分布为$b_i$，且满足$b_i\leq 0,\sum_i b_i=1$。则比赛结束之后，假设第j匹马赢得比赛，则资产可表示为$S(x(j))=b_jo_j$。经过n场比赛之后总资产可以表示为，
\begin{align}
S_n=\prod_{i=1}^n S(x_i).
\end{align}
注意到每一场比赛之间的结果是不会相互影响的，对应于深度学习中我们可以分batch进行采样和训练。
定义2：赛马的翻倍率(the doubling rate of a horse race)表示为,
$$W(b,p)=\mathbb{E}log_2(S)=\sum_{i=1}^m p_ilog_2(b_io_i).$$
与定义1相似，我们的目标是最大化赛马的翻倍率。具体地在赛马问题中，押注者可以采用部分财产进行押注并且保留剩余的财产，对应于深度学习中的m分类问题，模型即可以预测m个类别又可以预测为第m+1个类别来表示放弃预测。固定第m+1个类别的回报为1，那么根据定义2可以将优化问题表示为，
\begin{align}
max\ W(b,p)=\sum_{i=1}^m p_ilog_2(b_io_i+b_{m+1}).
\end{align}
上述也可以称为押注者损失函数(gambler's loss)。
2.2 - 将分类问题视为赛马问题
m分类问题可以视为寻找一个$\mathbb{R}^n\rightarrow \mathbb{R}^m$的映射函数$f$，其中$n$和$m$分别是输入维度和预测分类数。对于输出$f(x)$，我们假设其已经被标准化了，因此我们将$f(\cdot)$视为输入x划分为第j类的概率，表示为，
\begin{align}
Pr(j|x)=f(x)_j,
\end{align}
我们将映射函数$f$用参数为$w$的神经网络来建模，其输出为所有类别的概率分布。我们期望对于正确类别j进行极大似然化，则可以表示为，
\begin{align}
max\ \mathbb{E}[log\ p(j|x)]=\max_{w}\mathbb{E}[log\ f_w(x)_j],
\end{align}
对于m分类任务，我们加入额外的第m+1类表示放弃预测因此可将其转换为赛马问题。对于一个大小为B的mini-batch，假设所有类别的回报均为参数o，那么目标函数可以表示为，
\begin{align}
\max_{f}\ W(b(f),p)=\max_{w}\sum_{i}^Blog\left [f_w(x_i)_{j(i)}o+f_w(x_i)_{m+1}\right ],
\end{align}
其中i是batch中的第i个样本，$j(i)$是第i个样本的标签。$o$是一个超参数，其值越大则更加鼓励模型进行有效预测，否则将更倾向于放弃预测(第m+1类)。
2.3 -* 基于动态分配的在线硬样本挖掘（稍作改进）
我注意到，文中的方法虽然能够预测出样本的不置信分数，从而决定是否放弃预测，但没有对于高不置信的样本进一步进行挖掘。这里我称高不置信样本为硬样本，我认为在训练过程中不同难度的样本对于损失函数的贡献应该具有不同的权重，模型对于不确定的样本应该着重学习，而对于容易分类的样本应该降低其权重，因此我提出了一种称为基于动态分配的在线硬样本挖掘的学习策略。在训练过程中，根据样本的不置信程度调整样本对于损失函数贡献的权重，如下公式所示，
\begin{align}
w_i^{k,b}=1+\left (\frac{m_i^{k,b}-\frac{\sum_{j}^B m_j^{k,b}}{{\sum_{j}^B \mathbf{1}}}}{\sum_{j}^B m_j^{k,b}}\right ),
\end{align}
\begin{align}
l^{k,b}=\frac{\sum_i^B w_i^{k,b}l_i^{k,b}}{\sum_j^B \mathbf{1}},
\end{align}
其中$k$为第$k$个epoch，$b$为第$b$个batch，$i$为第$i$个样本，$m_i^{k,b}$为第$k$个epoch的第$b$个batch的第$i$个样本的评价指标，这里采用的是第(m+1)类的经过$softmax$标准化之后的预测分数作为评价指标，即预测的不置信程度，该评价指标越大，分配权重越大，$l_i^{k,b}$为第$k$个epoch的第$b$个batch的第$i$个样本的损失值，$l^{k,b}$为第$k$个epoch的第$b$个batch的损失值。
3 - 实验
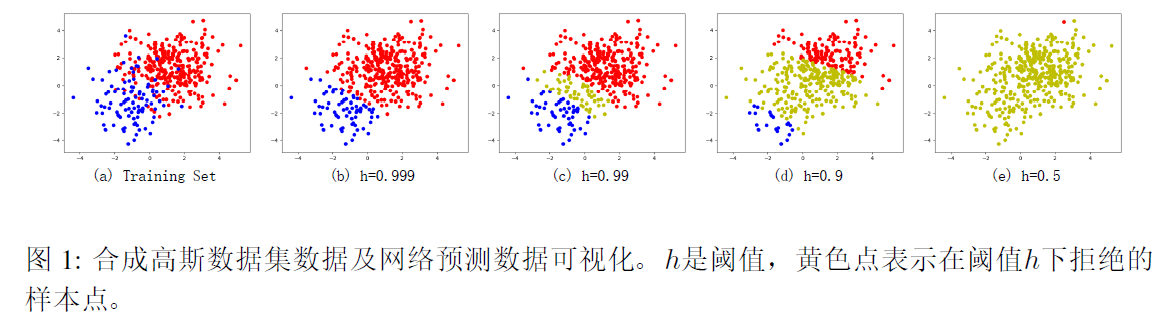
3.0 - 合成高斯数据集
