线性回归（Linear Regression）

0 - 基本问题

　　线性回归考虑的是有$n$个样本$\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\}$，每一个样本对应$m+1$维特征$\mathbf{x}_i=\{x_{i0},x_{i1},x_{i2},\cdots,x_{im}\}$（其中$x_{i0}=1$），记为$\mathbf{X}_{n\times (m+1)}$，且每一个样本都一个对应的标签，记为$\mathbf{y}_{n}$。需要找到参数$\mathbf{w}_{m+1}$，构造如下模型，

$$
h_{\mathbf{w}}\left(\mathbf{X}\right)=\mathbf{X}\mathbf{w}=\begin{pmatrix}
x_{10} & x_{11} & \cdots & x_{1m} \\ 
x_{20} & \ddots & \cdots & \vdots \\ 
\vdots & \cdots & \ddots & \vdots \\ 
x_{n0} & \cdots & \cdots & x_{nm)}
\end{pmatrix}\begin{pmatrix}
w_0\\ 
w_1\\ 
\vdots\\ 
w_m
\end{pmatrix},
$$

拟合出来的结果与真实目标之间的误差可以表示如下，

$$
J(\mathbf{w})=\frac{1}{2}\left(\mathbf{X}\mathbf{w}-\mathbf{y}\right)^T\left(\mathbf{X}\mathbf{w}-\mathbf{y}\right),
$$

其中，加入常数因子$\frac{1}{2}$是为了求导方便。

1 - 求解方法

1.1 - 最小二乘法

　　求解上述问题，等价于最小化$J(\mathbf{w})$，即令如下等式成立，

$$
\frac{\partial J}{\partial \mathbf{w}}=\mathbf{X}^T\left(\mathbf{X}\mathbf{w}-\mathbf{y} \right )=0,
$$

可经过如下变换解得$\mathbf{w}$，

$$\Leftrightarrow \mathbf{X}^T\mathbf{X}\mathbf{w}-\mathbf{X}^T\mathbf{y}=0,
\Leftrightarrow \mathbf{X}^T\mathbf{X}\mathbf{w}=\mathbf{X}^T\mathbf{y},
\Leftrightarrow \mathbf{w}^{*}=\left(\mathbf{X}^T\mathbf{X} \right )^{-1}\mathbf{X}^T\mathbf{y},$$

上述求解线性回归问题的方法即使最小二乘法（属于精确求解）。

1.2 - MLE

　　建设数据分布符合高斯分布（正态分布），那么模型误差也将符合高斯分布（正态分布），对于第$i$个样本的预测误差，有如下概率形式，

$$
P(y_i|\mathbf{x}_i,\mathbf{w})=\frac{1}{\sqrt{2\pi}\sigma }e^{-\frac{\left( y_i-\mathbf{x}_i\mathbf{w}\right)^2}{2\sigma^2}},
$$

那么，对于所有样本的预测误差，可以表示如下，

$$
l(\mathbf{w};\mathbf{y})\\=log L(\mathbf{w};\mathbf{y})\\=log\prod_{i=1}^{n}P(y_i|\mathbf{x}_i,\mathbf{w})\\=\sum_{i=1}^nlogP(y_i|\mathbf{x}_i,\mathbf{w})\\=\sum_{i=1}^nlog\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{\left(y_i-\mathbf{x}_i \mathbf{w}\right )^2}{2\sigma^2}} \\=nlog\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{2\sigma^2}\sum_{i=1}^{n}\left(y_i-\mathbf{x}_i\mathbf{w} \right )^2,
$$

令$\triangledown_{\mathbf{w}}l(\mathbf{w};\mathbf{y})=0$，通过如下过程可解得$\mathbf{w}$，

$$
\triangledown_{\mathbf{w}}l(\mathbf{w};\mathbf{y})=\frac{1}{\sigma^2}\mathbf{X}^T(\mathbf{y}-\mathbf{X}\mathbf{w})\\
\Leftrightarrow \mathbf{w}^{*}=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y},
$$

 上述结果表明，在高斯分布下的MLE和最小二乘法的求解结果是等价的（一个问题的多种角度）。

 1.3 - 梯度下降法

　　最小二乘法和MLE均为精确方法，但在实际求解过程中可能会有$\mathbf{X}^T\mathbf{X}$的逆不存在或者样本太多或者由于求解$\left(\mathbf{X}^T\mathbf{X}\right)^{-1}$时误差很大导致算法缺乏稳定性和可靠性等情况，因此精确方法不是万能的。梯度下降法是解决线性回归问题的常用的非精确方法（迭代法），其迭代公式如下，

$$
\mathbf{w}=\mathbf{w}-\alpha \triangledown J\left( \mathbf{w} \right )=\mathbf{w}-\alpha\mathbf{X}^T\left( \mathbf{X}\mathbf{w}-\mathbf{y}\right ),
$$

经过若干次迭代之后，即可得到逼近于最优值的$\mathbf{w}$。

2 - 线性回归的推广

下面介绍两种线性回归的推广方法：多项式线性回归以及广义线性回归。

2.1 - 多项式线性回归

　　上述的线性回归只适用于拟合多元一阶方程，这里举一个例子，方便后面讨论。例如对于有2个特征的第$i$个样本，上述线性回归可以描述为，

$$
y_i=w_0+w_1x_{i1}+w_2x_{i2}。
$$

　　为了拟合高阶多项式（这里以二阶为例），可以将模型改写为如下，

$$
y_i=w_0+w_1x_{i1}+w_2x_{i2}+w_3x_{i3}+w_4x_{i4}+w_5x_{i5},
$$

其中$x_1=x_1,\ x_2=x_2,\ x_3=x_1^2,\ x_4=x_2^2,\ x_5=x_1x_2$，可以发现，经过改写之后高阶多项式回归问题又可以用线性回归的方法进行解决。

2.2 - 广义线性回归

　　在实际问题中，往往$\mathbf{y}$与$\mathbf{X}$之间不满足线性关系，但是$\mathbf{y}$经过单调可微函数$g(\cdot)$的“激活”（在深度学习中常用的术语）之后，可以与$\mathbf{X}$满足线性关系。因此，可以将线性回归推广到广义线性回归，如下，

$$
g\left(\mathbf{y}\right)=\mathbf{X}\mathbf{w}^T,
$$

注意到，一般线性回归为当$g(\cdot)$为线性激活时的特殊情况。

3 - 正则化

　　考虑最小二乘法的求解公式，

$$
\mathbf{w}^{*}=\left(\mathbf{X}^T\mathbf{X} \right )^{-1}\mathbf{X}^T\mathbf{y},
$$

其中，当$\mathbf{X}$不是满秩或者某些列之间的线性相关性较大时，$\mathbf{X}^T\mathbf{X}$的行列式接近于0（即$\mathbf{X}^T\mathbf{X}$接近于奇异），此时计算$\left(\mathbf{X}^T\mathbf{X}\right)^{-1}$时的误差会很大，因此最小二乘法和MLE将缺乏稳定性和可靠性（不适定问题）。

　　要将不适定问题转化成适定问题，可以给损失函数加上一个正则化项，有如下两种方法：L1正则化和L2正则化。

3.1 - L1正则化（Lasso）

　　L2正则化即是给损失函数加上一个关于$\mathbf{w}$的二次正则项，如下，

$$
J(\mathbf{w})=\frac{1}{2}\left \|\mathbf{X}\mathbf{w}-\mathbf{y}^* \right \|^2_2+\lambda \left \| \mathbf{w}\right \|_1,
$$

注意到，该损失函数在$\mathbf{w}$处是不可导的，因此上述的所有方法均失效，可以采用坐标轴下降法或者最小角回归法进行求解（具体参考此博客）。

（注：Lasso回归可以使得一些特征的系数变小，甚至还是一些绝对值较小的系数直接变为0。增强模型的泛化能力。）

3.2 - L2正则化（Ridge，岭回归）

　　L2正则化即是给损失函数加上一个关于$\mathbf{w}$的二次正则项，如下，

$$
J(\mathbf{w})=\left \|\mathbf{X}\mathbf{w}-\mathbf{y}^* \right \|^2_2+\lambda \left \| \mathbf{w}\right \|^2_2,
$$

最小化$J(\mathbf{w})$，即令如下等式成立，

$$
\frac{\partial J}{\partial \mathbf{w}}=\mathbf{X}^T\left(\mathbf{X}\mathbf{w}-\mathbf{y} \right )+2\lambda\mathbf{w}=0,
$$

解得$\mathbf{w}^{ridge}=\left(\mathbf{X}^T\mathbf{X}+\lambda\mathbf{I} \right )^{-1}\mathbf{X}^T\mathbf{y}$。

（注：Ridge回归在不抛弃任何一个特征的情况下，缩小了回归系数，使得模型相对而言比较的稳定，但和Lasso回归比，这会使得模型的特征留的特别多，模型解释性差。）

4 - 代码

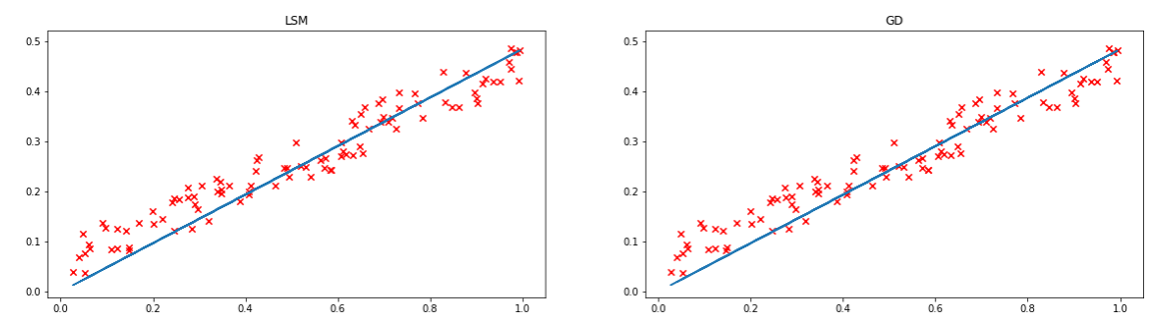
　　线性回归的python代码可见于我的github（实现了最小二乘法和梯度下降法），结果如下（LSM为最小二乘法，GD为梯度下降法）。

5 - 参考资料

https://www.cnblogs.com/huangyc/p/9782821.html

https://blog.csdn.net/ccnt_2012/article/details/81127117

https://blog.csdn.net/xgxyxs/article/details/79436195

https://blog.csdn.net/u012559269/article/details/80564606

https://github.com/czifan/Notebooks/tree/master/Linear%20Regression