前端基础--算法

排序

js本身数组的sort方法，可以满足日常很多需求。基本会写快速排序就够了

基本排序算法

基本排序的思想都很类似，基本都是一组嵌套的for循环，外循环便利数组的每一项，内循环用于比较

---

 

1.冒泡排序

冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。 它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。 走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。

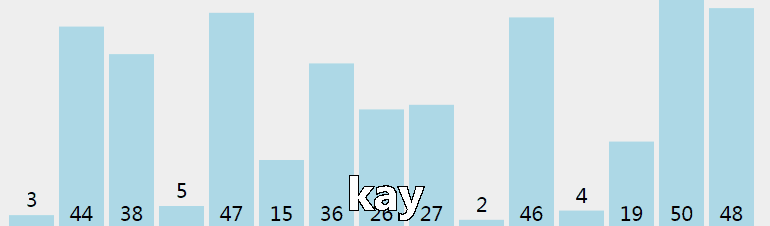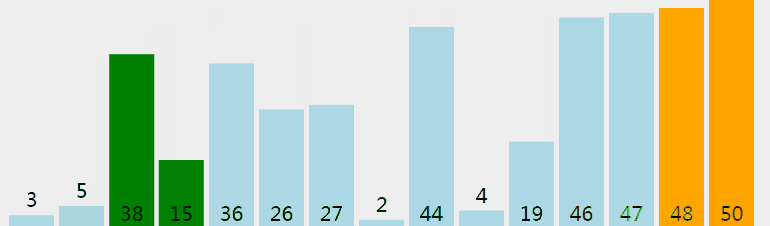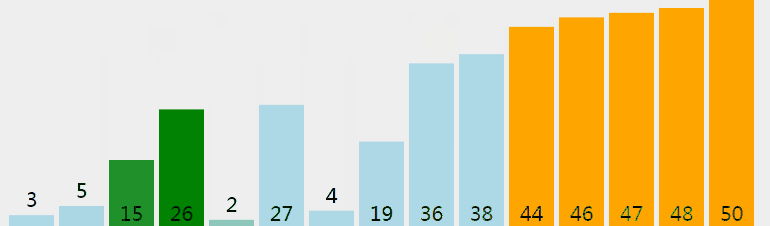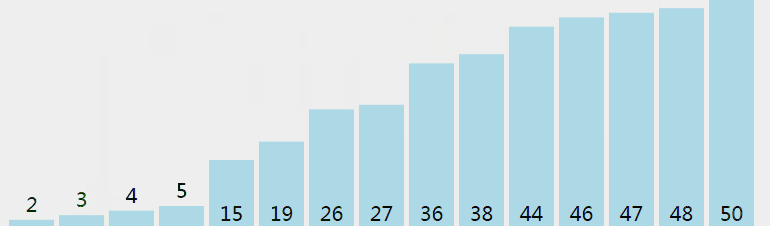
  function bubbleSort(arr) {
    let len = arr.length;
    console.log(arr)
    for (let outer = len; outer >= 2; outer--) {
      for (let inner = 0; inner < outer - 1; inner++) {
        if (arr[inner] > arr[inner + 1]) {
          // let tmp = arr[inner];
          // arr[inner] = arr[inner + 1];
          // arr[inner + 1] = tmp;
          [arr[inner], arr[inner + 1]] = [arr[inner + 1], arr[inner]]    // es6解构赋值
        }
      }
    }
    console.log(arr)
  }
  let arrs = [1, 56, 85, 3, 7, 3, 8]
  bubleSort(arrs)

注意点：

1.外层循环，从最大值开始递减，因为内层是两两比较，因此最外层 >=2 时即可停止；

2.内层是两两比较，从0开始，比较inner与inner+1，因此，临界条件是 inner<outer-1

在比较交换的时候，就是计算机中最经典的交换策略，用临时变量temp保存值.ES6可以用解构赋值简化。

---

 

2.选择排序

选择排序就是从数组头部开始，将第一个元素和其他元素比较，检查完所有的元素后，最小的放在第一个位置，接下来再开始从第二个开始，重复以上一直到最后。

  // 选择排序
  function selectSort(arr) {
    let len = arr.length;
    for (let i = 0; i < len - 1; i++) {
      for (let j = i + 1; j < len; j++) {
        if (arr[j] < arr[i]) {
          [arr[i], arr[j]] = [arr[j], arr[i]]
        }
      }
    }
    console.log(arr)
  }
  let arrs = [1, 56, 85, 100, 7, 3, 8]
  selectSort(arrs)

注意点：

1.外层循环的 i 表示第几轮，arr[i]表示房钱轮次最靠前的位置

2.内层从 i 开始，j 是 i 的下一位数，一次往后对比，找到小的，放到 i 位置，直到最后，arr[len-1]

时间复杂度

 基本排序算法，基本思想就是两层循环嵌套，第一遍元素O(n)，第二遍找位置O(n)叠加就是O(n2)

---

 3.高级排序

如果所有排序都像上面一样，对大量数据的处理，将是灾难性的。

快速排序【问的最多，快速排序】

快排是处理大数据最快的排序算法之一。它是一种分而治之的算法，通过递归的方式将数据依次分解为包含较小元素和较大元素的不同子序列。该算法不断重复这个步骤直至所有数据都是有序的。

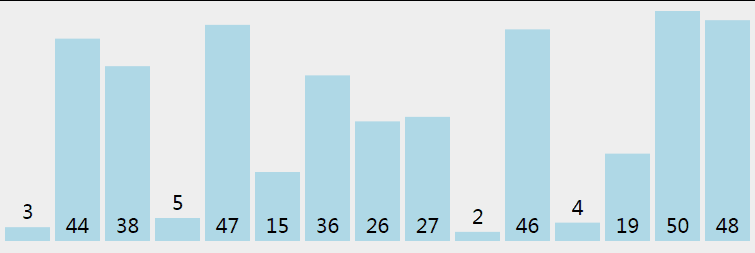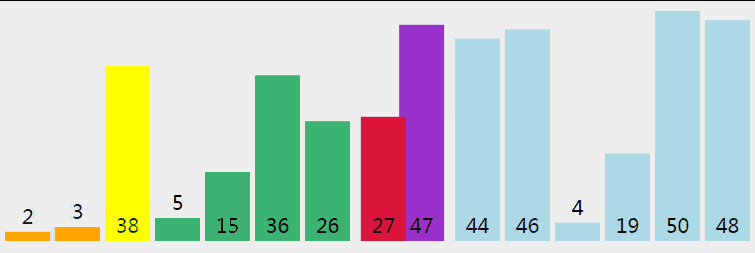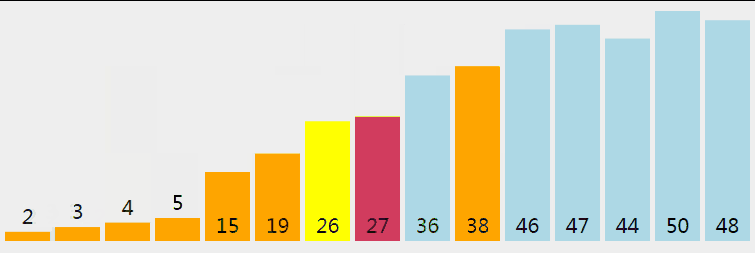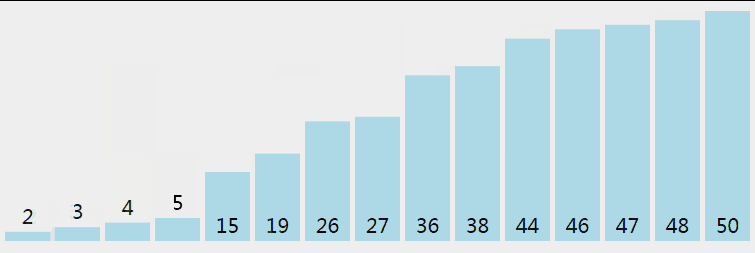
简单说： 找到一个数作为参考，比这个数字大的放在数字左边，比它小的放在右边； 然后分别再对左边和右变的序列做相同的操作:

1. 选择一个基准元素，将列表分割成两个子序列；
2. 对列表重新排序，将所有小于基准值的元素放在基准值前面，所有大于基准值的元素放在基准值的后面；
3. 分别对较小元素的子序列和较大元素的子序列重复步骤1和2

  // 快速排序
  function quickSort(arr) {
    if (arr.length <= 1) {
      return arr; // 递归出口
    }
    let left = [];
    let right = [];
    let current = arr.splice(0, 1);  // splice 后原arr会少一个，splice返回的是被删除的新的数组
    for (let i = 0; i < arr.length; i++) {  // 便利当前数组
      if (arr[i] < current) {
        left.push(arr[i]) // 放在左边
      } else {
        right.push(arr[i])  // 放在右边
      }
    }
    return quickSort(left).concat(current, quickSort(right)); // 递归，合并
  }
  let arrs = [1, 56, 85, 100, 7, 3, 8]
  let sum = quickSort(arrs)

---

时间复杂度总结

是否稳定

如果不考虑稳定性，快排似乎是接近完美的一种方法，但可惜它是不稳定的。 那什么是稳定性呢？

通俗的讲有两个相同的数A和B，在排序之前A在B的前面，而经过排序之后，B跑到了A的前面，对于这种情况的发生，我们管他叫做排序的不稳定性，而快速排序在对存在相同数进行排序时就有可能发生这种情况。

/*
比如对(5，3A，6，3B ) 进行排序，排序之前相同的数3A与3B，A在B的前面，经过排序之后会变成  
    （3B，3A，5，6）
所以说快速排序是一个不稳定的排序
/*

稳定性有什么意义？ 个人理解对于前端来说，比如我们熟知框架中的虚拟DOM的比较，我们对一个<ul>列表进行渲染，当数据改变后需要比较变化时，不稳定排序或操作将会使本身不需要变化的东西变化，导致重新渲染，带来性能的损耗。

辅助记忆

• 时间复杂度记忆
  • 冒泡、选择、直接 排序需要两个for循环，每次只关注一个元素，平均时间复杂度为O(n²)(一遍找元素O(n)，一遍找位置O(n)）
  • 快速、归并、希尔、堆基于二分思想，log以2为底，平均时间复杂度为O(nlogn)(一遍找元素O(n)，一遍找位置O(logn))
• 稳定性记忆-“快希选堆”（快牺牲稳定性）

---

递归

递归，其实是自己调用自己

 

递归步骤：

• 寻找出口：递归一定要有出口，锁定出口，保证不会死循环
• 递归条件：符合递归条件，自己调用自己

斐波拉契数列，每个语言讲递归都会从这个开始。前端可以从深度克隆说起。

Deep clone：实现一个对象的深度克隆

  // Deep Clone
  function deepClone(origin, target) {
    var target = target || {};
    for (let key in origin) {
      if (origin.hasOwnProperty(key)) {    // hasOwnProperty() 方法会返回一个布尔值，指示对象自身属性中是否具有指定的属性（也就是，是否有指定的键）。
        if (Array.isArray(origin[key])) { // 如果是数组，且嵌套
          target[key] = [];
          deepClone(origin[key], target[key])  // 递归
        } else if (typeof origin[key] === 'object' && origin[key] !== null) { //判断是对象嵌套对象的情况
          target[key] = {};
          deepClone(origin[key], target[key])  // 递归
        } else {
          target[key] = origin[key]   // 如果不是嵌套 ，就直接拷贝
        }
      }
    }
    return target
  }
  let a1 = { a: 1, b: 2, c: { c1: 4, c2: 8 } };
  let b1 = deepClone(a1);
  console.log(b1)

// 深浅拷贝还有参考：比如通常可以通过 JSON.parse(JSON.stringify(object)) 来解决。更多详情可去各大论坛。

上面的方法思路很清晰：

出口：遍历结束后 return

递归条件：遇到引用值Array 或 Object

参考例题：

Q1：Array数组方法的 flat 方法的实现，如：

Array
var arr1 = [1, 2, [3, 4]];
arr1.flat(); 
// [1, 2, 3, 4]

实现如下：

  Array.prototype.flat = function () {
    var arr = [];
    this.forEach((item, idx) => {
      if (Array.isArray(item)) {
        arr = arr.concat(item.flat()); // 递归去除数组元素
      } else {
        arr.push(item)  // 非数组直接push进去
      }
    })
    return arr;
  }

测试没问题

参考评论区另类解法。。

arr.prototype.flat = function() {
    this.toString().split(',').map(item=> +item )
}

toString方法，连接数组并返回一个字符串 '2,2,3,2,3,4'

split方法分割字符串，变成数组['2','2','3','2','3','4']

map方法，将string映射成为number类型2,2,3,2,3,4

Q3. 爬楼梯问题

有一楼梯共M级，刚开始时你在第一级，若每次只能跨上一级或二级，要走上第M级，共有多少种走法？

分析： 这个问题要倒过来看，要到达n级楼梯，只有两种方式，从（n-1）级 或 （n-2）级到达的。所以可以用递推的思想去想这题，假设有一个数组s[n], 那么s[1] = 1（由于一开始就在第一级，只有一种方法）， s[2] = 1（只能从s[1]上去 没有其他方法）。

那么就可以推出s[3] ~ s[n]了。

下面继续模拟一下， s[3] = s[1] + s[2]， 因为只能从第一级跨两步， 或者第二级跨一步。

function cStairs(n) {
    if(n === 1 || n === 2) {
        return 1;
    } else {
        return cStairs(n-1) + cStairs(n-2)
    }
}

Q4.二分查找

二分查找，是在一个有序的序列里查找某一个值，与小时候玩的猜数字游戏非常相啦：

A: 0 ~ 100 猜一个数字
B: 50
A: 大了
B: 25
A: 对头，就是25

因此，思路也就非常清楚了，这里有递归和非递归两种写法，先说下递归的方法吧：

• 设定区间,low和high
• 找出口： 找到target，返回target；
• 否则寻找，当前次序没有找到，把区间缩小后递归

function binaryFind(arr,target,low = 0,high = arr.length - 1) {
    const n = Math.floor((low+high) /2);　　　　　　// Math.floor() 返回小于或等于一个给定数字的最大整数。
    const cur = arr[n];
    if(cur === target) {
        return `找到了${target},在第${n+1}个`;
    } else if(cur > target) {
        return binaryFind(arr,target,low, n-1);
    } else if (cur < target) {
        return binaryFind(arr,target,n+1,high);
    }
    return -1;
}

接下来，使用循环来做一下二分查找，其实思路基本一致：

function binaryFind(arr, target) {
    var low = 0,
        high = arr.length - 1,
        mid;
    while (low <= high) {
        mid = Math.floor((low + high) / 2);
        if (target === arr[mid]) {
            return `找到了${target},在第${mid + 1}个`
        }
        if (target > arr[mid]) {
            low = mid + 1;
        } else if (target < arr[mid]) {
            high = mid - 1;
        }
    }
    return -1
}

---

参考链接：https://juejin.im/post/6844903656865677326