二分图最大匹配-增广路匈牙利算法
2022-12-25 作者:CZX
【二分图匹配问题】
匹配:二分图中 任意两条边没有公共点的边集 \({M}\)。
也就是说在这个边集中,每个节点只连一条边。
最大匹配问题:
- 二分图:选尽量多的边,任意两条边均没有公共点。
- 图中所有点都是匹配点,称为完美匹配。
若将点分为 \({X,Y}\) 集合,则若完美匹配,\({X}\) 集合中的匹配点 = \({Y}\) 集合中的匹配点。
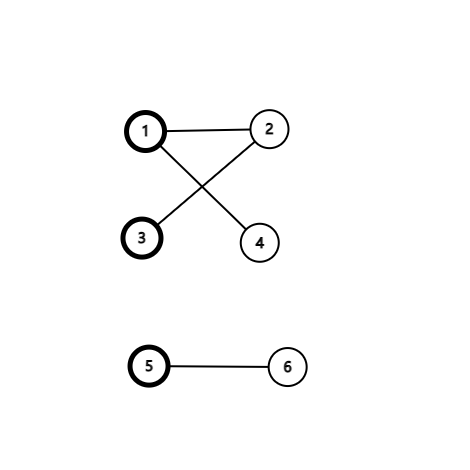
左边加粗点的是 \({X}\) 集合,右边未加粗的是 \({Y}\) 集合。
这幅图中,最大匹配数就是 \({3}\),边集 \({M{(1,4),(3,2),(5,6)}}\)
【增广路算法解决匹配问题】:
从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边...(注意顺序)
形成的路径叫交替路。两个端点(这条长路径的起点 终点)都是未匹配点,
这条路径就是增广路。
我们找到增广路后,将 匹配边 和 非匹配 边互换,
就会发现得到的匹配边比刚才多一条
(因为 非匹配边-匹配边-非匹配边...-非匹配边)开头和结尾都是 非匹配边,
所以非匹配边 比 匹配边要多一条 。
每次增广路走完,匹配边都增加了 \({1}\) 。
增广路没有后效性。
【增广路定理】:
如果不存在增广路,相当于存在最大匹配。
也就是说如果这个图的所有增广路都找完了,最大匹配也就找到了。
【增广路匈牙利算法】(梗概)
算法思路:
(1)置匹配集合 \({M}\) 为空
(2)找出一条增广路径 \({P}\),通过异或操作获得更大的匹配代替 \({M}\);
(3)重复(2)操作直到找不出增广路径为止。
二分图的规模一般都不大。
时间复杂度邻接矩阵:\({O(n^3)}\); 邻接表:\({O(mn)}\)
空间复杂度邻接矩阵:\({O(n^2)}\); 邻接表:\({O(m+n)}\)
【图解,跑一遍】
这里用“已”表示匹配边和匹配点,“未”表示非匹配边和未匹配点。
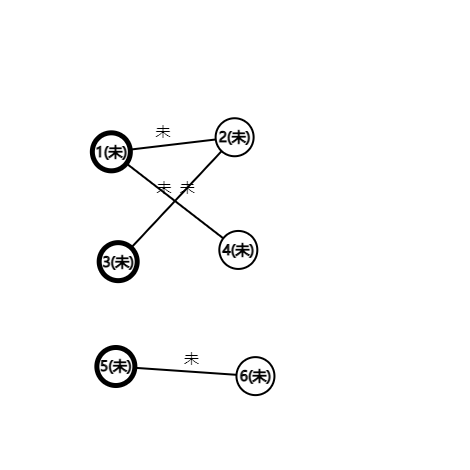
图1-一开始所有点都是未匹配点,所有边都是非匹配边
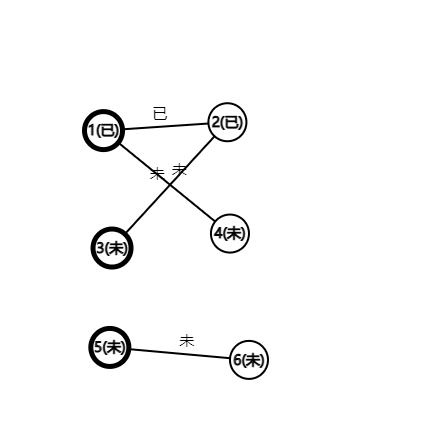
图2-从点 1 开始跑,\({(1,2)}\) 这条边是非匹配边,且起点和终点都是未匹配点,是增广路,按照增广路的操作改变,\({(1,2)}\) 变为匹配边,1 2 变为匹配点。
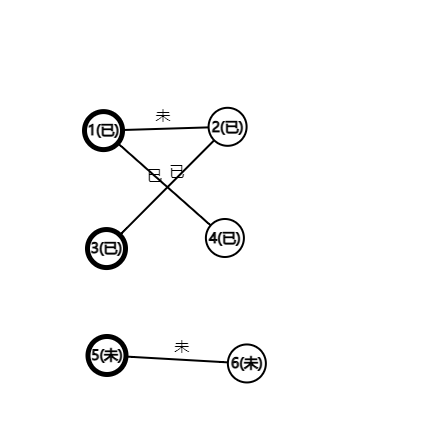
图3-(还没有运行的状态就是图二)执行点 3,走到点 2,发现点 2 已经匹配了。通过 2 走到 1,让 1 再找一个没有匹配的点。(如果这里没有点 4,那么点 3 就无法变成匹配点了)然后 1 找到了 4 。
我们发现 \({3-2-1-4}\) 正好是非匹配边-匹配边-非匹配边交替,且起点 3 ,终点 4 均为未匹配点,这是增广路,交换匹配边和非匹配边。完成后如图三所示。
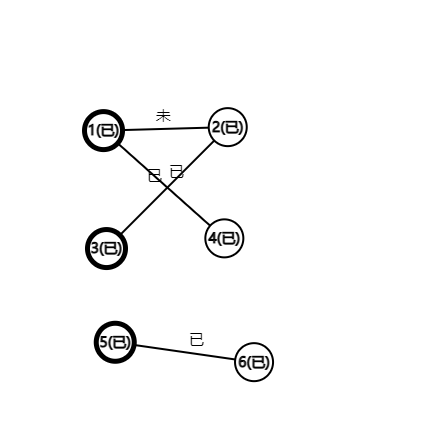
图4-5 再找到 6,完成匹配。
此时已经找不到增广路了,程序结束。
【例题】
有 \({n}\) 个女生 \({m}\) 个男生,他们之间有 \({k}\) 对相互认识
只有互相认识的异性才能一起跳舞。
求最多能一起跳舞的对数
(注意,既有 1 号男生,又有 1 号女生,所以 每一个号的性别都是不确定的,注意顺序!)
input:
3 2 5
1 4
1 5
2 4
output:
2
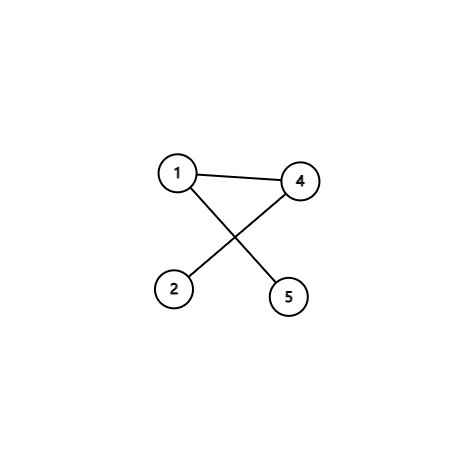
这里 \({1,2}\) 为男生,\({4,5}\) 为女生
分析一下,就是
给定一个二分图,其左部点的个数为 \({n}\),右部点的个数为 \({m}\),边数为 \({k}\),求其最大匹配的边数。
二分图匹配板子
注意,这里 \({k}\) 最后输入
这个题稍微改一下范围 输入格式就能过 P3386
下面给出两个版本:
邻接矩阵 & 邻接表(链式前向星)
邻接矩阵版
#include<iostream>
#include<cstring>
using namespace std;
int n,m,t,graph[101][101],link[101],vis[101];
// n:女生 m:男生 graph[u][v]: u 号男生认识 v 号女生
// graph[v][u]: v 号男生认识 u 号女生,二者并不一定同时存在
// 也就是说,第一个代表 男生 第二个代表女生
// link[i]:i 号男生暂时的女生舞伴
int find(int x){
// 给 x 号女生找舞伴
for (int i=1;i<=m;i++){
if (graph[x][i]&&vis[i]==0){
vis[i]=1; // 加 vis 的目的:增广路不重复经过一个节点
// vis 中的数据仅在本次搜索中有效,如果(在主函数中)调用 find ,vis 要清空
// vis[1] 代表的不是不能用了,被选中的男生还有可能改变舞伴
if (link[i]==0||find(link[i])){
/* 顺便提一嘴:如果前面 link[i]==0 满足了,那么后面的find函数不会执行
(即使执行 ,find(0) 也没啥用) */
link[i]=x;
return 1;
}
}
}
return 0;
}
int main(){
cin>>t>>n>>m;
for (int i=1;i<=t;i++){
int u,v;
cin>>u>>v; // 女 男
graph[u][v]=1;
// 注意,男 女的编号可能是重复的,这在样例中没体现,
// 绝对不能写 graph[u][v]=graph[v][u]=1;
}
int ans=0;
for (int i=1;i<=n;i++){
memset(vis,0,sizeof(vis)); // 这句必须要加,不加的话就无法改变增广路和匹配
/* 可以用 (1,3) (1,4) (2,3) 这个图来模拟一下
这个循环只会遍历n 即女生也就是 1 和 2
find(1) : 1 先把 3 置位舞伴,直接退出
find(2) : 2 遍历到 3 ,如果 vis 没有清空的话, vis[3] 此时就是 1
那么 find(2) 就直接结束了。
事实上,我们还要寻找增广路(进入第一层 if 然后 调用 find(1),发现 4 还可以做舞伴 )
所以 vis 一定要清空 */
if (find(i)){
ans++;
}
}
// cout<<endl;
for (int i=1;i<=m;i++){
cout<<link[i]<<' '<<i<<endl; // 这是输出 每个男生的配对
}
// 如果想看看女生的配对
// for (int i=1;i<=m;i++){
// link2[link[i]]=i; // 定义一下 link2
// }
// for (int i=1;i<=n;i++){
// cout<<link[i]<<' ';
// }
cout<<ans<<endl;
return 0;
}
链式前向星版
#include<iostream>
#define maxn 50001
#include<cstring>
using namespace std;
struct Edge{
int v,next;//终点 下一条边
}edge[maxn<<1];
int cnt,head[maxn],n,m,k,ans;
int link[maxn],vis[maxn];
void add(int u,int v){
edge[++cnt].v=v;
edge[cnt].next=head[u];
head[u]=cnt;
}
int find(int x){
int v;
for (int i=head[x];i;i=edge[i].next){
v=edge[i].v;
if (!vis[v]){
vis[v]=1;
if (!link[v]||find(link[v])){
link[v]=x;
return 1;
}
}
}
return 0;
}
int main(){
cin>>k>>n>>m;
int u,v;
for (int i=1;i<=k;i++){
cin>>u>>v;
add(u,v); // 同样,注意顺序
}
for (int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
if (find(i)){
ans++;
}
}
cout<<ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号