递归小结
递归小结
最大奇约数:
题目:
定义函数f(x)表示x的最大奇约数,这里x表示正整数。例如,f(20) = 5,因为20的约数从小到大分别有:1, 2, 4, 5, 10, 20,其中最大的奇约数为5。
给出正整数N,求f(1)+f(2)+…+f(N)
-
初看此题 盲目以为可直接用一函数求出从1 ~ n每一个数的最大奇约数 然后求和。思路乍看上去没问题,但10^9的数据规模实在恐怖 因此另辟蹊径
-
思路如下:
对于每一个奇数,其最大奇约数就是其本身。假若n为奇数,可求出f(1)+……+f(n)所有奇数项之和
即x^2 / 4。
对剩下的偶数进行处理。
对于每个偶数,其最大奇约数等于f(n / 2),因此,只需再处理s(n/2)
得到递归式:\[S(n) = n^2 / 4 + S(n/2) \]结束
集合的划分:
题目:
设S是一个具有n个元素的集合,S{a1,a2,….,an},现将S划分成k个满足下列条件的子集合S1,S2,…,Sk,且满足:
Si≠∅
Si∩Sj=∅ (1<=I,j<=k i≠j)
S1∪S2∪S3∪…Sk=S
则称S1,S2,…,Sk是集合S的一个划分。它相当于把S集合中的n个元素a1,a2,…,an放入k个(0<k<=n<30)无标号的盒子中,使得没有一个盒子为空。请你确定n个元素a1,a2,…,an放入k个无标号盒子中去划分数S(n,k)。
-
n个元素,划成k份,那么对于每个元素a,即有两种决策方法
1.在a处划分一个新集合
2.不在a处划分集合,将a并入后续集合中 -
共能划分k个集合,则设当前还能划分h个集合,还剩余l个元素
-
由其上推导可得,f(l,h) = f(l - 1,h - 1) + h * f(l - 1,h)
结束
分形图系列:
三道小题:
-
1.分形图
题目:
题目描述
分形(Fractal)通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”,即具有自相似的性质。例如一棵蕨类植物,仔细观察,你会发现,它的每个枝杈都在外形上和整体相同,仅仅在尺寸上小了一些。而枝杈的枝杈也和整体相同,只是变得更加小了。那么,枝杈的枝杈的枝杈呢?自不必赘述。图展示了4种类型的分形图。
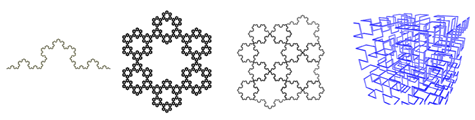
魔法世界的科学家由此提出分形宇宙论,即认为宇宙本质上是一个粒子。构成宇宙的无数个粒子里面又会有其他小宇宙。
例如:一个尺度的宇宙表示为:
X
两个尺度宇宙表示为
复制X X
X
X X
如果用B(n-1) 表示n-1尺度的宇宙,则递归定义为:
复制
B(n-1) B(n-1)
B(n-1)
B(n-1) B(n-1)
输入格式
输入有多组数据,每组一个整数n(n≤7),表示宇宙的尺度。
输出格式
每组数据以字母“X”绘出分形图,每组数据以一个“-”表示结束。
-
2.2的幂次方分解
题目:
任何一个正整数都可以用 22 的幂次方表示。例如 137=27+23+2^0137=27+23+20。
同时约定方次用括号来表示,即 a^b可表示为 a(b)。
由此可知,137可表示为 2(7)+2(3)+2(0)
进一步:
7= 22+2+20,并且 3=2+2^0。
所以最后 137 可表示为 2(2(2)+2+2(0))+2(2+2(0))+2(0)。
又如 1315=2^10 +2^8 +2^5 +2+1315=210+28+25+2+1
所以 1315 最后可表示为 2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)。
输入格式
一行一个正整数 n。
思路:
首先,容易想到,对于每一个正整数,都可以将其拆分为一个二次幂和另一个数(可以为0)的和。
那么,便可以先将一个数这样拆分,接着处理剩下的那一部分和拆出来的幂(次数也可以进行这样的拆分)
完美的递归模型!
但需要特别注意括号的输出
#include<bits/stdc++.h> using namespace std; int n; void change(int m){ int x = m,cnt = 0; while(x != 0){ x /= 2; cnt++; } cnt--;//特别注意要将cnt减一,诸如此类的计数,都会多算一次,不过可以用do while语句来进行修改,以减少此类错误发生 x = m - pow(2,cnt); if(cnt == 0){ cout << "2(0)"; } else if(cnt == 1){ cout << "2"; } if(cnt > 1){ cout << "2("; change(cnt); cout << ")"; } if(x > 0){ cout << "+"; change(x); } } int main(){ cin >> n; change(n); return 0; } -
3.对称
题目:
题目描述
FJ非常喜欢对称。他在一块NM的土地上进行一种叫“放奶牛”的活动,首先他找到一个在这块NM这块土地上的一块最中心的点(所谓最中心,要求这个点不仅要是行的最中心点,同时也要是列上的最中心),在这个点上放上奶牛,然后这个点会把NM的这块土地分成完全相等的4块,然后FJ会对这4块继续做以上的行动。如果不存在这样的中心点,或者区域已成为11则停止。
比如如下的例子,N=7,M=15,于是FJ在第4行,第8列放了一个奶牛。此后,分出了4块37的更小的土地。对于37的小土地,它会继续进行如图以下的分解。直到不能继续分解为止。
............... ............... .......|....... .C.|.C.|.C.|.C. ............... ............... ...C...|...C... ---C---|---C--- ............... ............... .......|....... .C.|.C.|.C.|.C. ............... -> .......C....... -> -------C------- -> -------C------- ............... ............... .......|....... .C.|.C.|.C.|.C. ............... ............... ...C...|...C... ---C---|---C--- ............... ............... .......|....... .C.|.C.|.C.|.C.最后一共放置了21头奶牛。 对于给出的N*M的地图,要求输出最后一共能在这个地图上放置多少只奶牛。
输入格式
第一行两个数,N,M
输出格式
最终放置的奶牛数。
当时做的时候确实是糊涂了。对于拆下来的每一块建立坐标系,如若其长或宽为偶数,那么直接返回,依次递归进行
不用记录地图!!!
斐波那契数列:
第一个月一对兔子(刚出生),每对兔子两个月后便可以生一对兔子,恰好一雌一雄。六个月后丧失生育能力,八个月后死亡,求第n个月时有多少兔子?
构建递推式即可
在递归中,如何记录经过的数据?
如题:
题目描述
已知 n 个整数 x1,x2,……,xn以及 11个整数 k(k<n)。从 n 个整数中任选 k 个整数相加,可分别得到一系列的和。例如当 n=4,k=3,4 个整数分别为 3,7,12,19 时,可得全部的组合与它们的和为:
3+7+12=22
3+7+19=29
7+12+19=38
3+12+19=34
现在,要求你计算出和为素数共有多少种。
例如上例,只有一种的和为素数:3+7+19=29
输入格式
第一行两个空格隔开的整数 n,k(1≤n≤20,k<n)。
第二行 n个整数,分别为 x1,x2,……,xn(数据范围)。
输出格式
输出一个整数,表示种类数。
如何记录这种情况是否处理过呢?
首先可以想到,这三个数的和可能是相同的,因此可以抓住这点来存储每一种状态。但显而易见的是,在x != y != z != l != m != n的情况下, x + y + z
仍有可能等于l + m + n。
那么我们就可以将每个数以幂的形式存储起来,拉大差距,即x^a + y^a + za,a越大,xa + y^a + z^a = l ^a + m^a + n^a的概率也就越低了,也就可以达到存储状态的目的。
但这种存储方法有一种缺点就是会占用大量的内存,时间复杂度会出奇的高(当让也可以通过其他方式来存储状态,例如状态压缩)
也可以用动态数组或bool数组等方式进行记录,暂且不提
另一种独辟蹊径的方式就是,既然可能会重复,那么为何不试着使计算不重复呢?
如下代码
#include<cstdio>
#include<cmath>//引入头文件
using namespace std;
int n,k,a[21],s=0,ans=0;//定义全局变量,方便写函数
bool f[21];//判断该数有没有被选过,用bool型变量
int ss(int x)//定义判断素数的函数
{
if(x==1||x==0)return 0;//考虑特殊情况(虽然和为1或0不太可能,但还是要预防一下极品数据)
for(int i=2;i<=sqrt(x);i+=1)//sqrt为平方根函数,需要调用cmath库,sqrt(x)用处详解请见上
//从2开始循环是因为任何一个数mod(就是%)1都等于0
if(x%i==0)//一旦发现该数能mod尽除1和它本身的数,立即返回0
return 0;
return 1;//若一直运行到i==sart(x)时都没有退出,则该数为素数,自动返回1
}
int xs(int x,int y)//该函数是本程序中最关键的部分,认真看哦
{//x为已经选了几个数,y为选第几个数
for(int i=y;i<=n;i+=1)//从y~n循环是为了避免重复的出现,例如1234中,选3个,已经选过123
(持续更新中ing)
最后
那么对于递归,其要素又在哪里呢?
首先,将一个小规模的问题替换题目,再用一个规模稍大的来替换,从中发现规律,即子问题构型!
通过子问题构型,即可确定递归式
接下来,确定递归的边界条件,一个递归的大致框架就好了。
但同样重要的,还要确定形参的意义。好的形参能方便思考,简化代码,因此得慎重考虑。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号