第一阶段复习——动态规划2
状态压缩动态规划
就是对状态做一个压缩，一般是用二进制表示，比如
P1896 [SCOI2005] 互不侵犯
每一行的状态一般来说要开好多维数组，然而一个二进制就搞定了。
预处理：首先 1<<n 范围枚举状态，筛选出合法状态，记录每一个合法状态的点数。
设 \(f_{i,j,k}\) 表示前 i 行，放 j 个士兵，当前行的状态是 k 的方案数。初始化 \(f_{0,0,0}=1\)。
转移：
对于前i行，放j个士兵的情况，考虑转移。双重循环枚举状态，分别用a和b表示（a循环在外），用c记录a状态的士兵数。
进行判断：如果j不小于c；正对判断；错位判断（位运算的巧用）。如果都满足，则 \(f_{i,j,a}=f_{i-1,j-c,b}\)
具体见代码。
最后有一个技巧，多算一层，直接输出 \(f_{n+1,k,0}\) 就可以，虽说并没有节省时间复杂度。
P1879 [USACO06NOV] Corn Fields G
和上一个问题的区别就在于约束条件，变成了十字形的，另外还加了一个贫瘠土地的限制。
判断条件：!(s[a] & s[b]) && (s[a] & g[i]) == s[a]
第一个的意义是水平判断，和上题一样；第二个是障碍判断，位运算巧用。
滚动数组的另一种操作方法，用与运算来维护，每次更新 \(i\oplus 1\) 的位置就好。
P2704 [NOI2001] 炮兵阵地
十字形的约束扩大了一层。
\(f_{i,a,b}\) 表示前i行，第i行是状态a，第i-1行是状态b的方案数。
判断：
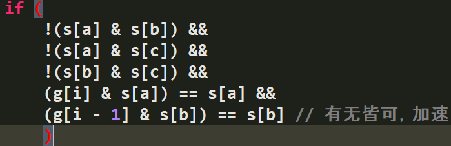
但这里面有一些冗余，删除之后：（因为比较状态合法只需要a-b,a-c之间合法，b-c就合法；另外，b这一层在a的上一层，b肯定已经被算过合法状态了，所以转移一定不会出现不合地图的情况，所以不用判断b的地图合法性）
转移：
\(f[i \& 1][a][b] = \max(f[i \& 1][a][b], f[(i - 1) \& 1][b][c] + num[s[a]])\)
将第一维压缩为两个位，与运算交替，可以通过此题。
一些习题
P2622 关灯问题II；PRZ；P3694 邦邦的大合唱站队；P3092 [USACO13NOV] No Change G；P5005 中国象棋 - 摆上马
关灯问题
这题是求一个最小步数类型的题。设计状态 f[state] 表示state状态的最少步数，然后跑bfs就可以。但是重点在于处理操作。发现一个操作序列用一个二进制好像是无法表示的，那么就开两个。opt1用来搞1->0，opt2用来搞0->1。
下一个状态的获取：t = (u | opt1[i]) & (~opt2[i])
详细解释：
这个位运算操作可以做到将操作序列O(n)处理降到O(1)。但这个思路很nb。
首先考察这个操作的意义，对于一个操作序列：其中的1表示把当前状态u中对应位置的1变成0；-1表示把当前状态u中对应位置的0变成1；0表示无影响。
首先-1的意义可以想到或运算：将u和opt1[i]进行按位或，因为或运算只有在序列位置为1，u位置为0的时候起作用，因为序列中只有需要更改的地方是1，其余地方都是0，无影响！所以考虑需要更改的地方，正好。之后再考虑1操作，将1变成0，用~opt2[i]和u进行与运算，注意这个opt序列中也只有需要更改的信息，其他都是0，但是与运算的性质是1不变性，0必变性，所以要取反，这里1变为0,0仍然是0。
[能力提升综合题单Part4 动态规划2]
区间dp
石子合并
重点在于如何识别出来这道题是动态规划，即快速证伪贪心。因为只能取相邻两堆的限制，导致不能做到每次取到最小和。
破环成链复制一倍。
对于f[l][r]表示l~r的最小代价，g可以设为最大代价，这里我们只考虑f的转移，g同理。
对于区间dp的常见方法就是外层枚举跨度，内层枚举左端点，最内层枚举中间点。
那我们考虑f可以由中间点怎么转移得来。
\(f[l][r] = \min(f[l][k] + f[k][r] + s[r] - s[l - 1])\)
合并的代价是每次都有的，直接前缀和就好了。
最后枚举答案需要i从1~n枚举，然后跨度为n去选，因为复制了一倍。
能量项链
这题一样
有一个极简的写法：
for(int len = 3; len <= n + 1; len++)
for(int i = 1, j; (j=i+len-1) <= 2 * n; i++)
for(int k = i + 1 ;k < j; k++)
f[i][j] = max(f[i][j], f[i][k] + f[k][j] + a[i] * a[k] * a[j]);
习题
P4290 [HAOI2008] 玩具取名；两道棋盘分割。
洛谷题单：【动态规划3】区间与环形动态规划
括号序列！
[HAOI2008] 玩具取名
这道题上来就想区间dp，然而实现的时候用的map和set，复杂了，tle半天。其实这个合并判断的处理用一个三维小数组就足够了。
本质就是区间dp，状态转移数组是 f[l][r][k]， 还是布尔型的。
注意字符串从0开始，改成字符数组可以实现从1开始。
数位dp
三道例题
数字游戏1；数字游戏2；windy数。
练习
AHOI同类分布；手机号码
参考OIwiki的解说和习题。hm的ppt。
习题
usaco：P7415 P9129 P6006 P3607，这几道是guide上的，题解也在上面。
