第一阶段复习——基础动态规划
背包知识点总结：
- 01背包、完全背包的转移方程
- 滚动数组和倒序
- 初始化问题：完全放满和不一定放满
- 多重背包二进制优化，边界问题。处理完之后跑完全背包。“在这一讲中，我们看到了将一个算法的复杂度由 O(V ΣMi) 改进到 O(V ΣlogMi) 的过程，还知道了存在复杂度为 O(V N) 的算法。 ”单调队列仍不会
- 二维费用背包，仍可以套用01或完全的思路，滚动数组、辅助数组或者逆序
- 01背包方案数和最优方案数，dx
- 小优化：费用高还价值低的物品，可以删去。
- 有依赖的背包问题
- 泛化物品
参考：背包问题九讲。
有依赖的背包问题：金明的预算方案。
更一般地，附件也可以有自己的附件，这样就构成了森林，需要树形dp。
背包一些变化
输出方案
可以用一个辅助数组g[i][j]记录0和1，表示状态f[i][j]转移的时候选择了前一项还是后一项，即是否选择第i件物品。
输出字典序最小的方案
方案总数
\(f_{i,j}=f_{i-1,j}+f_{i-1,j-c_i}\)
初始条件是 \(f_{0,0}=1\)
最优方案总数
开一个 g[i][j]，如果f[i][j]由不选i转移来，则g就从g[i-1][j]转移来；否则从g[i-1][j-ci]转移来。
结合容斥原理
例题：硬币购物
c是不变量，d是变量。设si为事件，然后容斥展开。
发现，对于xi>di的这样的事件是很好求的，即 \(f_{s-c_i\times (d_i+1)}\)，x1>d1且x2>d2就是 \(f_{s-c_1\times(d_1+1)-c_2\times(d_2+1)}\)
注意一些细节：容斥枚举方法，外层循环i枚举状态数，内层用sign=-sign更新符号位
一些例题：
旅行商的背包；多人背包；P2851 [USACO06DEC] The Fewest Coins G；CF-Checkout Assistant；P2732 [USACO3.3] 商店购物 Shopping Offers；P4516 [JSOI2018] 潜入行动
算法竞赛进阶指南。
树形dp
树的三个重要对象
1.重心
重心的5个性质证明要学会。可以参考suxxsfe的博客。
例题两道：Link Cut Centroids; Kay and Snowflake
2.直径
树的直径可以有边权。
两种方法的思路。
两遍dfs的思路有一个重要的证明，就是证明第一次dfs一定可以找到直径的一端。
dp方法：记录d1、d2两个变量（可以是数组）记录当前子树中最大和次大向下链，拼凑答案。这里有个理解上的误区，总觉得在u点可以往上走，但是其实向上的链在u的祖先就已经处理过了，这是错觉。所以要注意，树形dp的重点就在于单独处理每个点和处理点和祖先之间的影响关系。
代码：
直径有一个性质：直径必重合，而多条直径必交于中点。
证明：感性理解就是调整一下，如果稍加偏离中点扔成立，则出现新的直径，矛盾。
另一种证明：首先证明直径必相交（反证）；然后证明多条直径情况下一个中点一定在另一个直径上（否则又出现更优）；再证明中点重合。
OI-wiki也有一个证明。
3.中心
到最远叶子距离最短的点是中心。
性质：中心一定在直径上，（不是在直径中点呢？）
如果中心不在直径上
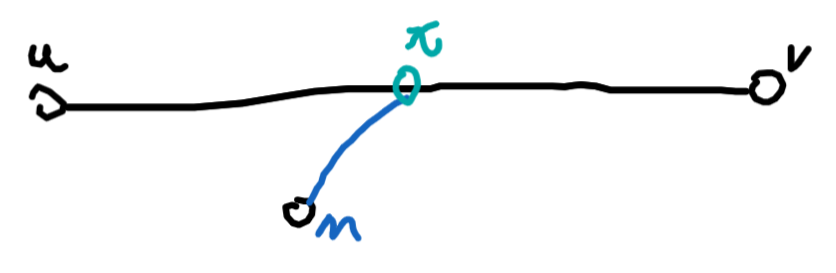
设x在(u,v)路径上，不妨设x到v的路径最长（显然），那么x一定比M更优。
一些题
P2014 [CTSC1997] 选课；Centroids；CSP2019 树的重心
杂
P2656 采蘑菇
