第一阶段复习——最短路
最短路部分
最小环
一些细节:枚举最小环是依据还没有更新经过k的最短路,所以要写在更新经过k的最短路之前。要判断是否存在路径。ijk三指针需要i与k、j与k相连。
传递闭包
f[i][j] |= f[i][k] & f[k][j];
注意是有向图
Dij证明
命题:在取出最短路长度最小的节点u的时候,u的最短路已经被确定,即D(u)=dis(u)
证明:设u是算法中第一个在加入S集合时不满足D(u)=dis(u)的点。(u的存在性略)。一定存在一条路径s→x−y→u,其中y是路径上第一个属于T集合的点。而x和y直接相连,显然x∈S。
因为D(x)=dis(x),所以(x,y)会被松弛,于是加入u的时候,一定有,D(y)=dis(y)
因为边权为正,所以D(y)≤D(u),从而dis(y)≤D(y)≤D(u)≤dis(u)。但因为u被取出,所以dis(u)≤dis(y),故D(u)=dis(u),与假设矛盾。命题得证。

反图
负环
例题:拉近距离


最短路计数
方法:因为不涉及权值,所以单纯bfs就好。自环不会影响结果,因为如果经过自环,一定比不经过自环要长,所以输入判自环。重边会影响结果,但是一样计入即可(可不可以用乘法什么的优化)。在遇到一个没访问过的点时,一定是最短路,更新即可,该点的计数+=前驱的计数;若遇到访问过的点,且该点最短路长度大于前驱最短路长度(其实这两个长度必定只差1),则依然更新,其他情况都不是最短路,不更新。这题做完了。
次短路
例题:[USACO06NOV]Roadblocks G
- 首先想到在最短路算法的过程中计算次短路。进而想到开两个数组,一个是dis1用来存最短路,一个是dis2用来存次短路。
- 更新最/次短路是最重要的一点。
- 对于u向v的更新:(定义折线长度为u点最短路加(u,v)边权)
- 判断1:如果dis1[v]可以更新,则更新dis1[v] 。(这里可以加一句,让dis2[v]等于先前的dis1[v] )
- 判断2:如果dis1[v]不能更新(这不代表dis2[v]不能更新)。那么如果折线长度小于dis2[v],而且折线长度大于dis1[v](这个dis1[v]并没有被更新,注意这里的逻辑),则更新dis2[v]为折线长度。
- 判断3:注意到判断2中更新dis2[v]的是最短路的折线长度,这一定比次短路的折线长度更优,所以判断2若不成立,那么才考虑,用次短路的折线长度更新。换个角度理解,这个算法其实是两次松弛,判断2保证了严格小于最短路的次短路。
- 对于三个判断,有一个成立,就要入队。因为更新势必造成对之后的影响,就要入队。而且从if,else if的角度也很好理解。
- 这里可以发现,判断123是转折的,可以用else-if连接,比方说,判断2成立,判断3就一定不成立。
- 好在该题可以一条边重复走。
分层图的几个典例
最短路结合二分
例题:通往奥格瑞玛的道路
边权是扣的血量。点权是要花的路费。
那肯定是最短路和边权有关。
二分最小花费,每次跑一次最短路。
单调性:最短路长度与花费呈非严格单调递减。
曾经的分析:
- 这题属于“求最大值的最小值”题型,那么就要考虑二分答案——对过路费进行二分答案,二分的板子一定要备好。进而考虑check函数,check函数就是dijkstra,不过要满足最短路长度要小于b,就是血量不能扣光。
- “我们假设需要的钱”越多,能走的点也就越多,可以走到终点的可能性也就越大。这里过路费的最大值和扣血量是有单调关系的。假设ans是过路费最大值的最小值,那么一定有一条小于b的路径L到终点。假设一个允许的过路费最大值k>ans,那么走L仍然满足。
有一些小细节要注意:
- 每一次dij,要判断起点的费用,否则WA一个点。if (f[1] > x) return false; // 记录1
- 输出AFK的条件有不少:(1)l>maxf;(2)dis[n]>=b(单数会WA一个点);(3)Dijkstra(100000100)。 总之,边界处理太困难了。
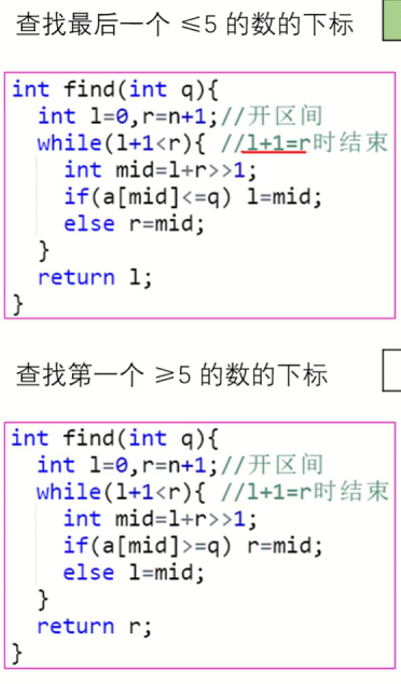
差分约束系统
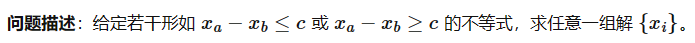
c是正的。x是整数。
连边,加一个超级源点防止图不连通并赋dis=0x3f,或将每个点入队并赋dis=0
跑一遍最短路。
如果有负环出现,则无解;如果无负环,则dis[i]就是解。

例题:模板题、小K的农场。
小K的农场这道题可以把 xa=xb转化cheng xa-xb<=0
奇偶性
例题:P5663 [CSP-J2019] 加工零件
- 好像有一种分层图的做法。(Froggy)
- 一般做法:计算出dis_odd,和dis_even。对于每一组a, l:如果l是奇数,那么考虑有没有小于等于l的dis_odd[a],有就是yes;如果l是偶数,那么考虑有没有小于等于l的dis_even[a],有就是yes。否则就是no。
- 计算dis_odd, dis_even,由于边权是1,采用01bfs就可以。
- 注:01bfs中,dis_even,dis_odd初始设为0x3f3f3f除了dis_even[1]=0。好像还有一个孤立点的情况。
TODO: P7997 [WFOI - 01] 刷题 (problem)
正、反图 记忆化搜索
例题:P3953 [NOIP2017 提高组] 逛公园
两遍最短路,求出1到各点的最短路,和各点到n的最短路。这道题卡dijkstra,用spfa就可以了。(见鬼)
然后考虑dfs,处在u点,考虑邻接的v点,用x,w(u,v),dis_anti[v]三段拼凑答案。x是上层传下来的路径长度,这里我已开始搞错了,写成了dis_ord[u],然而并不是这样的,因为如果这样,枚举到的路径只有一段是不一样的,会漏掉很多。
那么就超时了。记忆化搜索,设f[u][t]表示在u点,“消耗了”t个k值,之后的方案数。很巧妙,cjh的方法。我觉得,“消耗”可以替换成“还剩多少k值”。
注:还要做一些剪枝,比如没有路走、路径超过D+k等等。
关于0环:0环是导致无穷解的原因。注意到,从0环上任意一点u出发回到u时,其x值不会变。所以用d[u]数组记录u点第一次被访问的x值,用flg[u]记录u点被访问次数。若flg[u] != 0 && d[u] == x,则存在0环。
参考:cjh的ppt
建模
例题:P1875 佳佳的魔法药水
DP
例题:物流运输


 浙公网安备 33010602011771号
浙公网安备 33010602011771号