P4568 [JLOI2011] 飞行路线

分层图算法

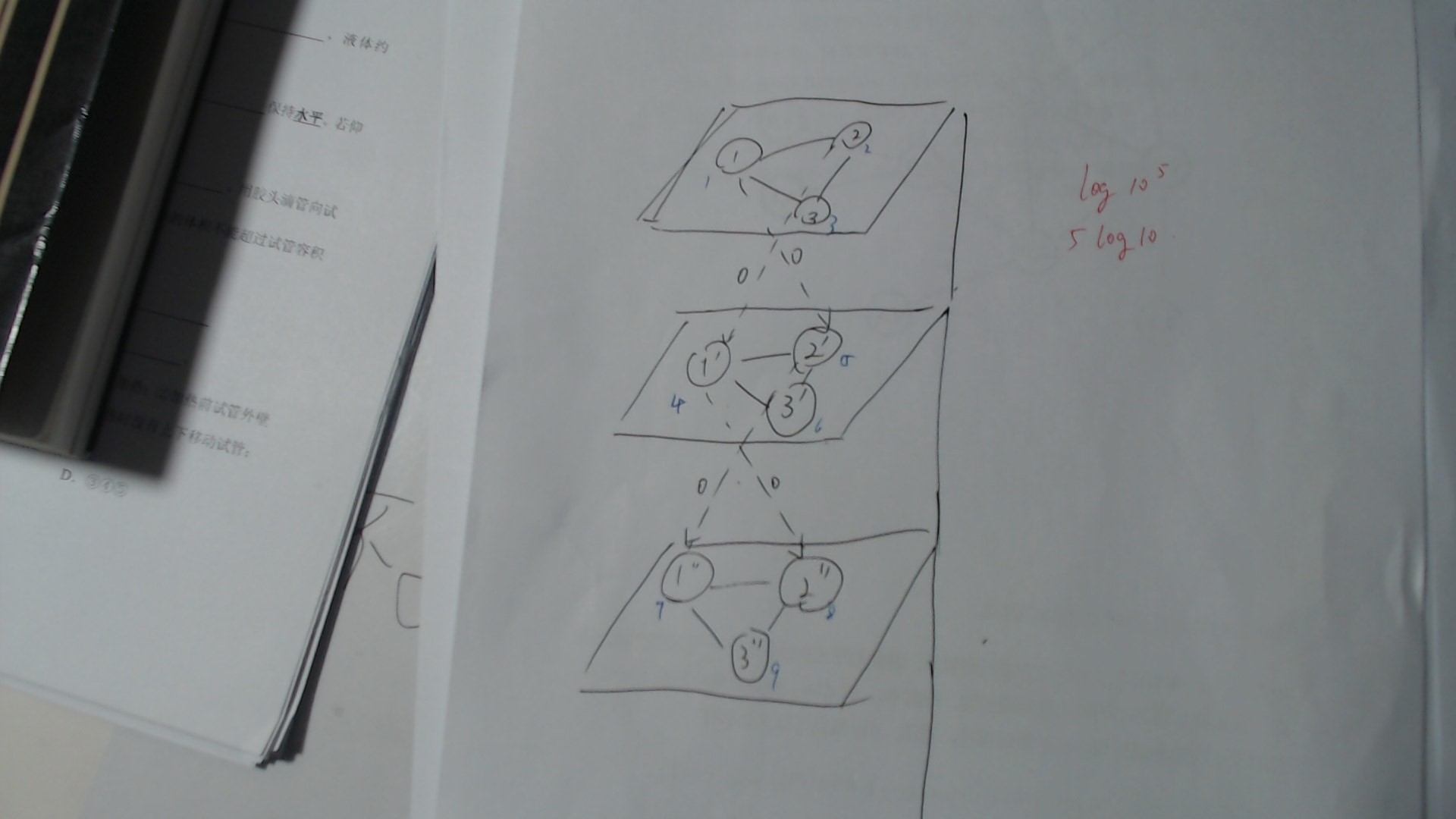
将图分为 \(k\) 层，层之间连权值为 \(0\) 的边，跑一遍 dij 就好了。目前已近学会了基本分层图建法，anguei的偏dp思维还需要掌握。

类似的题目还有 P4822 [BJWC2012]冻结

#include <bits/stdc++.h>

using namespace std;
int n, m, k;
const int maxn = 200005;
struct edges{
	int to, w;
};
// n 10^4, m 5* 10^4
vector<edges>e[maxn]; // k * n的范围
priority_queue<pair<int, int> > q;
bitset<maxn>vis;
int dis[maxn];
void dj(int start)
{
	memset(dis, 0x3f, sizeof(dis));
	dis[start] = 0;
	q.push(make_pair(-dis[start], start));
	while (q.size()) {
		int u = q.top().second; q.pop();
		if (vis[u]) continue;
		vis[u] = true;
		for (edges ed : e[u]) {
			int v = ed.to, w = ed.w;
			if (dis[v] > dis[u] + w) {
				dis[v] = dis[u] + w;
				q.push(make_pair(-dis[v], v));
			}
		}
	}
}
int main()
{
	int s, t;
	scanf("%d%d%d", &n, &m, &k);
	scanf("%d%d", &s, &t);
	for (int i = 1, _, __, ___; i <= m; i++) {
		scanf("%d%d%d", &_, &__, &___);
		e[_].push_back({__, ___});
		e[__].push_back({_, ___});
		// construct layered graph
		for (int layer = 1; layer <= k; layer++) {
			// ed in layer
			e[_ + layer * n].push_back({__ + layer * n, ___});
			e[__ + layer * n].push_back({_ + layer * n, ___});
			// ed between layers
			e[_ + (layer - 1) * n].push_back({__ + layer * n, 0});
			e[__ + (layer - 1) * n].push_back({_ + layer * n, 0});
		}
	}
	for (int i = 1; i <= k; i++) {
		e[t + (i - 1) * n].push_back({t + i * n, 0});
	}
	dj(s);
	printf("%d\n", dis[t + k * n]);
	return 0;
}