P1829 [国家集训队]Crash的数字表格 / JZPTAB

莫比乌斯反演

$\color{red}{f(n)=\sum\limits_{d|n}g(d) \Leftrightarrow g(n)=\sum\limits_{d|n}\mu(d)f(\dfrac{n}{d})}$

$f(n),g(n)$ 均为积性函数。

$f(n)$ 称为 $g(n)$ 的莫比乌斯变换。

$g(n)$ 称为 $f(n)$ 的莫比乌斯逆变换。

这里需要复习一下狄利克雷卷积和常用卷积关系： $(f*g)(n)=\sum\limits_{d|n}f(d)g{(\dfrac{n}{d})}=\sum\limits_{d|n}f(\dfrac{n}{d})g{(d)}$

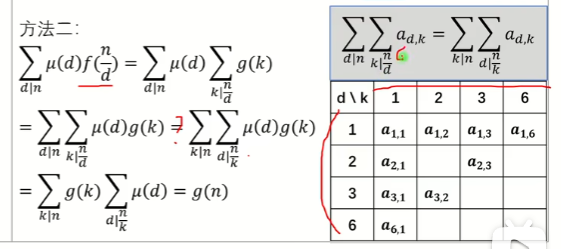
于是推证莫比乌斯反演：

若 $f=g * 1$，则 $\mu * f = \mu * g * 1 = g * \mu * 1 = g * \varepsilon = g$

若 $g=\mu*f$，则 $g*1=\mu*f*1=f*\mu*1=f*\varepsilon=f$

此处有一个nb的证明方法，我并没有太懂

例题

P1829 [国家集训队]Crash的数字表格 / JZPTAB

给出 $n,m$，求 $\sum\limits^n_{i=1}\sum\limits^m_{j=1}lcm(i,j)\pmod{20101009}$，数据规模 $n,m\le 10^7$

分析：

$\color{red}{[\gcd(i,j)=1]=\sum\limits_{d|gcd(i,j)}\mu(d)}$

代码实现：calc函数 $O(\sqrt{N}*\sqrt{N})=O(N)$，init函数 $O(N)$

#include <algorithm>
#include <cstdio>
using namespace std;
const int N = 10000010;
const int P = 20101009;
int vis[N], p[N], mu[N], S[N], cnt;

void init()
{
    mu[1] = 1;
    for (int i = 2; i < N; ++i)
    {
        if (!vis[i])
            p[++cnt] = i, mu[i] = -1;
        for (int j = 1; i * p[j] < N; ++j)
        {
            vis[i * p[j]] = 1;
            if (i % p[j] == 0)
                break;
            mu[i * p[j]] = -mu[i];
        }
    }
    for (int i = 1; i < N; ++i)
        S[i] = (S[i - 1] + 1LL * mu[i] * i * i % P + P) % P;
}
int G(int n, int m)
{
    return (1LL * n * (n + 1) / 2 % P) * (1LL * m * (m + 1) / 2 % P) % P;
}
int F(int n, int m)
{
    int res = 0;
    for (int l = 1, r; l <= n; l = r + 1)
    {
        r = min(n / (n / l), m / (m / l)); // 分块的灵活运用
        res = (res + 1LL * (S[r] - S[l - 1]) * G(n / l, m / l) % P + P) % P;
    }
    return res;
}
int calc(int n, int m)
{
    if (n > m)
        swap(n, m);
    int res = 0;
    for (int l = 1, r; l <= n; l = r + 1)
    {
        r = min(n / (n / l), m / (m / l));
        res = (res + 1LL * (r - l + 1) * (l + r) / 2 % P * F(n / l, m / l) % P) % P;
    }
    return res;
}
int main()
{
    init();
    int n, m;
    scanf("%d%d", &n, &m);
    printf("%d\n", calc(n, m));
}