普通生成函数
生成函数（Generating Function）
某个序列 \(a\) 的生成函数是一种形式幂级数，其每一项的系数可以提供关于这个序列的信息。我们只关注系数，指数是用来构造的
普通生成函数：\(F(x)=\sum_{n\ge 0}a_nx^n\)
\(a_n\) 可以是有穷序列也可以是无穷的。例如：
\(<1,2,3>\longrightarrow 1+2x+3x^2\)
\(<1,1,1,\cdots>\longrightarrow 1+x+x^2+\cdots = \sum_{n\ge 0}x^n\)
\(<1,2,4,8,\cdots>\longrightarrow 1+2x+4x^2+8x^3\cdots = \sum_{n\ge 0}2^nx^n\)
加减运算
\(F(x)\pm G(x) = \sum_{i\ge 0}a_ix^i\pm \sum_{j\ge 0}b_jx^j=\sum_{n\ge 0}(a_n\pm b_n)x^n\)
因此 \(F(x)\pm G(x)\) 是 \(<a_n\pm b_n>\) 的普通生成函数。
乘法运算（卷积）
\(F(x)G(x) = \sum_{i\ge 0}a_ix^i\sum_{j\ge 0}b_jx^j=\sum_{n\ge 0}x^n\sum^n_{i=0}a_ib_{n-i}\) （令 \(i+j=n\)）
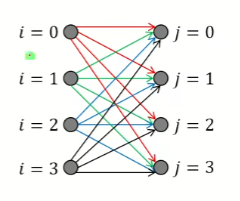
因此 \(F(x)G(x)\) 是序列 \(<\sum^n_{i=0}a_ib_{n-i}>\) 的普通生成函数
普通生成函数的用处：解决多重集组合数的问题。
问题：有 \(n\) 种物品，每种物品 \(a_i\) 个，问取 \(m\) 个物品的组合数？
设从每种物品种取 \(b_i\) 个，\(0\le b_i\le a_i\)，\(m=\sum^n_{i=1}b_i\)，对于一组选定的 \(b_i\) 进行组合的方案数为 \(1\)。例如 3 个 A、1 个 B 的方案就是AAAB；取 2 个 A、2 个 B 的方案就是AABB。
构造生成函数：第 1 种物品的生成函数为 \(1+x^1+x^2+\cdots+x^{a_1}\)，第 \(n\) 种物品的生成函数为 \(1 + x^1 + x2 + \cdots + x^{a_n}\)。即 \(\prod\limits^n_{i=1}\sum\limits^{a_i}_jx^j\)，求 \(x^m\) 的系数。
注意指数即物品个数，系数即组合数。
例如，有 3 种物品，分别有 3，2，1 个，问取4 个物品的组合数？
枚举的话，有AAAB、AAAC、AABB、AABC、ABBC，5个方案。
构造：\(\left(1+x+x^2+x^3\right)\left(1+x+x^2\right)(1+x)\\\begin{aligned}& =\left(1+x+x^2+x+x^2+x^3+x^2+x^3+x^4+x^3+x^4+x^5\right)(1+x) \\ & =\left(1+2 x+3 x^2+3 x^3+2 x^4+x^5\right)(1+x) \\ & =\left(1+x+2 x+2 x^2+3 x^2+3 x^3+3 x^3+3 x^4+2 x^4+2 x^5+x^5+x^6\right) \\& =\left(1+3 x+5 x^2+6 x^3+5 x^4+3 x^5+x^6\right)\end{aligned}\)
例题：HDU-2152 Fruit
int n, m;
int a[110], b[110], c[110], d[210];
int calc()
{
memset(c,0,sizeof(c)); memset(d, 0, sizeof(d));
for (int i= a[1]; i <= b[1]; ++i)
c[i] =1; // 填充第一个括号
for (int i = 2; i <= n; i++) { // n 个物品
for (int j = 0; j <= m; j++) { // 第m个物品，后面的不用算
for(int k = a[i]; k <= b[i]; k++) {
d[j + k] += c[j]; //d是辅助数组，类似高精乘法。
}
}
for (int j = 0; j <= m; j++) {
c[j] = d[j];
d[j] = 0;
}
}
return C[m];
}
HDU-1085 Holding bin-Laden Captive!
面值为1,2,5的硬币分别有 \(a_1,a_2,a_3\) 枚，问用这些硬币不能组成的最小面值是多少？
中国剩余定理？
构造生成函数：\(\prod_{i=1}^{n}\sum^{c_ia_i}_{j=0}x^j\)，\(c\) 是单张面值。从小到大遍历系数，为 0 的那一项就是答案。这里的指数是面值，系数是方案。
\(k\) 的循环需要注意。
for(int k = 0; k <= a[i] * b[i] && j + k <= m; k += b[i]) {
d[j + k] += c[j];
}
