树的直径算法
树上任意两节点之间最长的简单路径即为树的「直径」。记 \(\delta(s, t)\) 为树的真实直径。
算法1,两遍dfs
首先从任意节点 \(y\) 开始进行第一次 DFS,到达距离其最远的节点,记为 \(z\),然后再从 \(z\) 开始做第二次 DFS,到达距离 \(z\) 最远的节点,记为 \(z'\),则 即为树的直径。
那么为什么此算法可行?
我们只需证明对于任意一点 \(x\) 经过第一次dfs之后到达的点 \(y\) 一定是 \(\delta(s,t)\) 的一端 \(s\) 或 \(t\)。
定理:在一棵树上,从任意节点 \(x\) 开始进行一次 DFS,到达的距离其最远的节点 \(z\) 必为直径的一端。
我们采用反证法。记出发点为 \(y\),真实直径 \(\delta(s,t)\),设从 \(y\) 进行的第一次dfs到达的距离其最远的点 \(z\) 不为 \(t\) 或 \(s\)。
那么有三种情况:
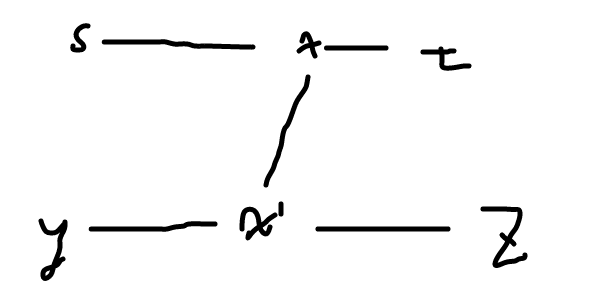
- 若 \(y\) 在 \(\delta(s,t)\) 上:那么 \(\delta(y,z)>\delta(y,t)\Rightarrow \delta(x,z)>\delta(x,t)\Rightarrow \delta(s,z)>\delta(s,t)\) 矛盾。其中 \(x\) 是 \(\delta(s,t)\) 上一中转点
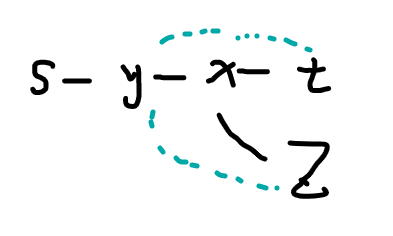
- 若 \(y\) 不在直径上,且 \(\delta(y,z)\) 与 \(\delta(s,t)\) 有重合路径
那么 \(\delta(y,z)>\delta(y,t)\Rightarrow \delta(x,z)>\delta(x,t)\Rightarrow \delta(s,z)>\delta(s,,t)\) 矛盾。- 若 \(y\) 不在 \(\delta(s,t)\) 上,且 \(\delta(y,z)\) 与 \(\delta(s,t)\) 不存在重复路径:
那么 \(\delta(y,z)>\delta(y,t)\Rightarrow \delta(x',z)>\delta(x',t)\Rightarrow\delta(x,z)>\delta(x,t)\Rightarrow\delta(s,z)>\delta(s,t)\)矛盾。- 三种情况都矛盾,得证。
注意负权边不适用
那么代码实现就很简单了
const int N = 10005;
int n, c, d[N];
vector<int> e[N];
void dfs(int u, int fa) {
for (int v :e[u]) {
if (v == fa) continue;
d[v] = d[u] + 1;
if (d[v] > d[c]) c = v;
dfs(v, u);
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d %d", &u, &v);
e[u].push_back(v), e[v].push_back(u);
}
dfs(1, 0);
d[c] = 0, dfs(c, 0);
printf("%d\n", d[c]);
return 0;
}
\(O(N)\)?
树形dp
每个节点作为子树的根向下,所能延伸的最远距离 \(d1\),和次远距离 \(d2\),那么直径就是所有 \(d1+d2\) 的最大值。
树形 DP 可以在存在负权边的情况下求解出树的直径。
const int N=10010,M=20010;
int n,a,b,c,ans;
struct edge{int v,w;};
vector<edge> e[N];
int dfs(int x,int fa){
int d1=0,d2=0;
for(auto ed : e[x]){
int y=ed.v, z=ed.w;
if(y==fa) continue;
int d=dfs(y,x)+z;
if(d>=d1) d2=d1,d1=d;
else if(d>d2) d2=d;
// printf("回%d d1=%d d2=%d\n",x,d1,d2);
}
ans=max(ans,d1+d2);
// printf("离%d ans=%d\n",x,ans);
return d1;
}
int main(){
cin>>n;
for(int i=1; i<n; i++){
cin>>a>>b>>c;
e[a].push_back({b,c});
e[b].push_back({a,c});
}
dfs(1,-1);
cout << ans << endl;
return 0;
}
最后的最后,始终要记住,树是无环的,这一性质很重要,在两个算法中都用到了。
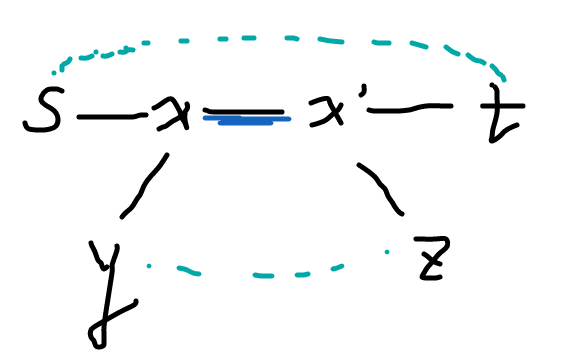

 浙公网安备 33010602011771号
浙公网安备 33010602011771号