辗转相除的时间复杂度

$\gcd(a,b) = \gcd(b,a\%b)$

这是辗转相除法，也叫欧几里得算法

欧几里得算法的时间复杂度我们认为是 $O(log n)$ 的。

证法1

设 $a>b$

分为两种情况：

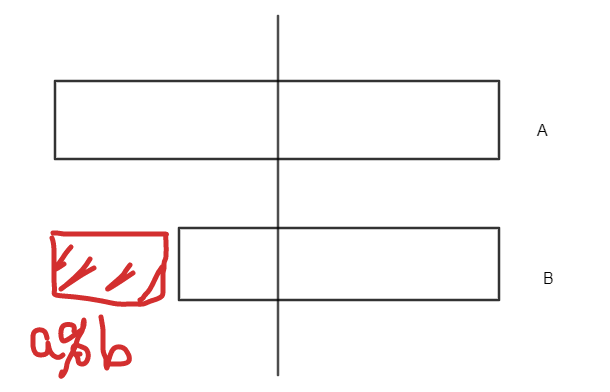
① $a>2b$

发现缩减速度大于等于2倍，问题规模缩小至少一半

② $a<2b$ 即 $a>b>\frac{a}{2}$

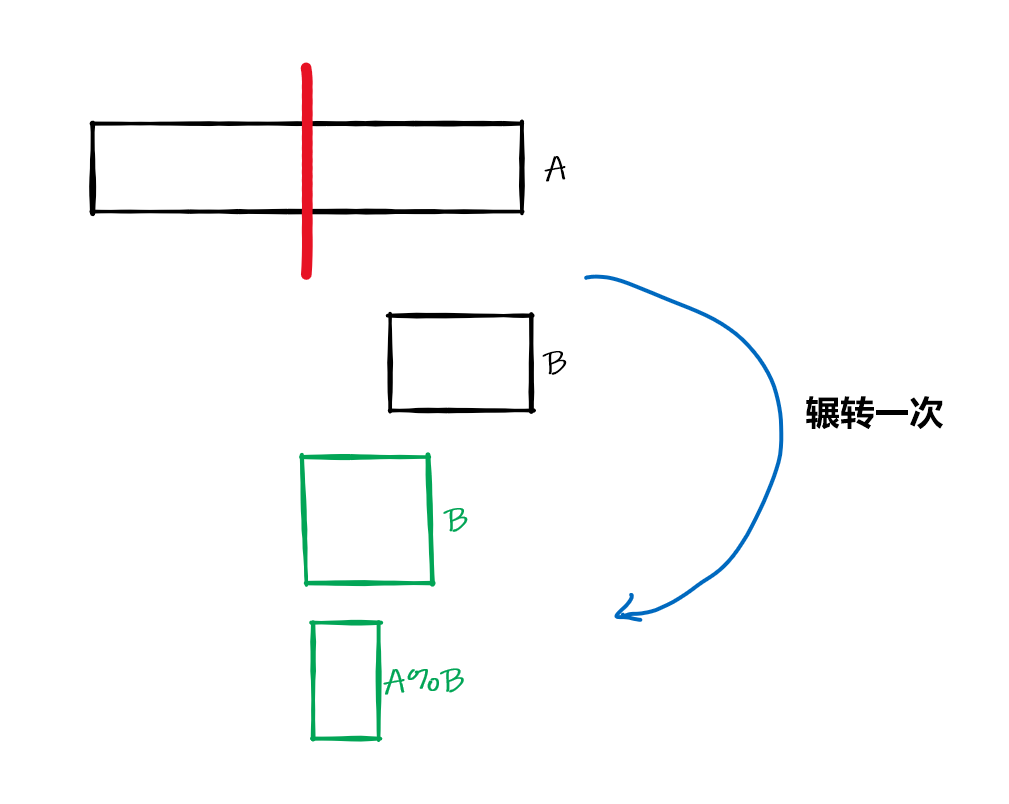
考虑算两下，$(a,b)=(b,a\%b)=(a\%b,b\%(a\%b))$

发现辗转两次之后，问题规模也一定至少缩小了一半。

所以 $\log n \le T \le 2\log n$，忽略常数姑且算为 $\log n$

证法2

这个方法更为严谨，用斐波那契数列证明的，还没学会……

---

最后学会了一个斐波那契数列的快速算法，记录一下

pair<int, int> fib(int n) {
  if (n == 0) return {0, 1};
  auto p = fib(n >> 1);
  int c = p.first * (2 * p.second - p.first);
  int d = p.first * p.first + p.second * p.second;
  if (n & 1)
    return {d, c + d};
  else
    return {c, d};
}