人生如此复杂，机会多得像稠密图，我们没理由认输。尽管我们走不了最短路，但图仍是连通图。TLE之前，没有一个节点叫失败。(You know what's cooking? BOOM~~)!

2019 年 10 月训练赛(10.30早)

2019 年 10 月训练赛(10.30早)

A1.数据结构

题目背景

引言

数据结构学的好，未来工作没烦恼。

Edgration 是一个喜欢乱搞数据结构的蒟蒻（以下简称edt），有一天，他作死想去***难一下dalao：

edt想求一种数据结构，使得可以实现区间加，求出某一区间大于k的元素的个数

dalao1：sb线段树

dalao2：sb分块

dalao3：sb平衡树

edt: 不行，那就加上取模，求区间取膜mod后大于MIN小于MAX的元素个数

dalao1：线段树&……￥#&……%……&*&%￥

dalao2：sb分块 &%￥……%#￥#&……&*

dalao3：*&……%&￥LCT维护SBT水题 &……%&……%

edt：那不仅取模，每个数乘上数组下标再取模

dalao：￥%￥￥&*（#￥% 叽里呱啦叽里呱啦

edt：不行，在把取模的值丢到一棵树上，维护一棵仙人掌乘积方差的最小极差

dalao：替罪羊树上用sb块状链表维护Toptree上的最小费用最大流和可持久化仙人掌，算出来在基尔霍夫矩阵中反演后跑一遍fft维护的插头DP就好了，给我三分钟轻松水过。。

edt：mmp

题目描述

蒟蒻Edt把这个问题交给了你 ———— 一个精通数据结构的大犇，由于是第一题，这个题没那么难。。

edt 现在对于题目进行了如下的简化：

最开始的数组每个元素都是0

给出n，opt，mod，min，max，mod在int范围内

操作A，Q

A: L,R,X 表示把[l,R]这个区间加上X

（数组的从L到R的每个元素都加上X）

Q: L,R 表示询问[L,R]这个区间中元素T满足 min<=(T∗i%mod)<=max 的 T这样的数的个数（i是数组下标）

（元素的值*数组下标%mod在min到max范围内）

由于 edt 请来了一位非三次元的仓鼠，他帮你用延后了部分问题，将这些询问打入了混乱时空，你的询问操作不会超过1000次，不幸的是，对于延后的询问操作可能有很多次（小于1e7次），但是保证这些延后的询问操作之后不会再次有修改操作

（就是在最后会有很多次询问，但不会进行修改）

输入格式

给出n，opt，mod，min，max表示序列大小，操作次数，取膜，最小值，最大值

下面opt行，给出

A： L，R，X表示区间加，保证X在int范围内(<2147483647）

Q：L，R表示区间查询满足条件的个数

再给出一个Final值，表示后面有Final个询问

下面Final行，给出

L，R表示询问区间[L,R]之间满足条件的个数

输出格式

每行对于每个QQ操作输出QQ个数表示每次询问的值，

下面Final行表示Final个询问的值

输入样例#1： 
 
3 2 4 0 2
A 1 3 5
Q 2 3 
5
1 3
2 3
1 1 
2 2 
3 3
输出样例#1： 
 
1
2
1
1
1
0
输入样例#2： 
 
17 25 4098 310 2622
A 10 16 657212040
A 4 15 229489140
A 1 2 -433239891
A 3 12 532385784
A 10 17 56266644
A 8 10 10038874
A 6 9 13084764
A 4 5 -9206340
Q 2 8
A 2 4 -43223955
A 6 9 31478706
A 2 4 189818310
A 2 8 179421180
A 2 8 40354938
Q 8 14
A 3 6 57229575
A 6 13 132795740
A 2 17 14558022
A 14 15 -552674185
A 5 11 -1104138
Q 2 12
Q 1 14
A 3 9 524902182
A 8 12 114291440
A 3 7 107531442
1
11 12
输出样例#2： 
 
3
6
7
8
2
输入样例#3： 
 
20 3 4317 1020 2232
A 8 15 -434078222
A 1 2 54988154
A 13 19 81757858
15
7 11
3 5
3 9
6 9
9 13
6 19
1 20
3 5
3 10
1 7
2 14
6 10
2 3
2 3
10 12
输出样例#3： 
 
0
0
0
0
0
2
2
0
0
0
0
0
0
0
0

说明

样例说明

给出样例1的解释：

样例1中，a数组修改为5，5，5

每个a[i]*i%4 的值为1,2,3

对于Final的询问

询问[1，3]中大于等于0小于等于2的个数为2个

剩下的询问类似

题目说明

注意：

1.关于负数取模问题，请以 c++ 的向0取整为标准，即如：

[-7 %3==-1 ] [7 %3==1 ]

2.一共会有50个测试点，每个点分值为2分。

因为测试点数较多，请oier们自觉地不要故意多次提交来卡评测机，出题人 edt 在这里表示由衷的感谢

数据范围

如果你不能作对所有点，请尝试获得部分分，所有数据都是随机生成

 

对于前面的修改和询问用差分解决，后面的final个数较多，用前缀和预处理后解决

 

//
#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define ull unsigned long long
template <typename T>
inline void rd(T& x)
{
    char ch=getchar();
    bool sign=true;
    while(!isdigit(ch))
    {
        if(ch=='-')sign=false;
        ch=getchar();
    }
    for(x=0; isdigit(ch); ch=getchar())x=x*10+ch-'0';
    if(!sign)x=-x;
}
ll n,opt,Mod,Min,Max,l,r,xx,Left,key,Final;
ll sum[80005];
int sum2[80005];
//inline ll ksc(ll x,ll y,ll p)负数不能用。。。。
//{
//    ll z=(ld)x/p*y;
//    ll res=(ull)x*y-(ull)z*p;
//    return (res+p)%p;
//}
int main()
{
//    freopen("datastruct.in","r",stdin);
//    freopen("datastruct.out","w",stdout);
    //cin>>n>>opt>>Mod>>Min>>Max;
    rd(n),rd(opt),rd(Mod),rd(Min),rd(Max);
    char a;
    for(int j=1; j<=opt; j++)
    {
        Left=0;
        key=0;
        cin>>a;
        if(a=='A')
        {
            rd(l),rd(r),rd(xx);
            sum[l]+=xx;
            sum[r+1]-=xx;
        }
        if(a=='Q')
        {
            rd(l),rd(r);
            for(int i=1; i<l; i++)
                Left+=sum[i];
            for(int i=l; i<=r; i++)
            {
                Left+=sum[i];
                if((i*Left)%Mod>=Min&&(i*Left)%Mod<=Max)
                {
                    key++;
                }
            }
            cout<<key<<endl;
        }
    }
    Left=0;
    for(int i=1; i<=n; i++)
    {
        Left+=sum[i];
        if((i*Left)%Mod>=Min&&(i*Left)%Mod<=Max)
        {
            sum2[i]=1;
        }
        sum2[i]+=sum2[i-1];
    }
     rd(Final);
    for(int i=1; i<=Final; i++)
    {
        rd(l),rd(r);
        cout<<sum2[r]-sum2[l-1]<<endl;
    }
}

 

B2.答案错误

每道WA了的题都会有一个分数，对于两个人的WA题程度是否相同，小X有这样一个评判方法：

无聊的她想了这样一个神奇的函数

 

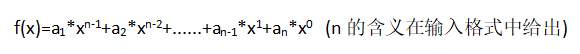
她认为，无论ai取什么值，两组f(x)的和都相等，则这两组题的错误程度很相似

假如有分值为 A={1,4,6,7 } ，B={2,3,5,8} 的两份被篡改完成的WA题，当a1=a2=a3=1时，神奇的函数为

f(x)=x^2+x+1

那么，f(1)=3,f(2)=7,f(3)=13......

显然 f(1) + f(4) + f(6) + f(7) = 124 = f(2) + f(3) +f(5) +f(8)

对于这组系数，此分组方案是合法的，可以证明，a_iai​取任意值，按照以上方案分组都满足条件（两组的f(x)f(x)和相同），不信可以手动枚举（_hua|ji_）

所以，A={1,4,6,7 } ，B={2,3,5,8}就是一种合法的分组

输入格式

第一行一个整数nn，代表有2^n2n道WA题，分值分别从1到2^n， n>=2 (emmm........满分是inf)

第二行一个整数q，表示有q组询问

最后一行q个整数，询问分值为x的WA题是谁的名字

（因为小X比较菜，所以我们认为分值为1的WA题是属于她的）

输入样例#1：
 
3
2
4 5
输出样例#1： 
 
X
Z
输入样例#2： 
 
4
10
1 5 1 5 9 9 3 1 6 1
输出样例#2： 
 
X
Z
X
Z
Z
Z
Z
X
X
X

说明

对于10%的数据，n<=4 , q<=10;

对于40%的数据，n<=20 , q<=5000;

对于100%的数据，n<=60 , q<=1000000;

 

一道正解比暴力还短的水题

——其实就是等幂和问题

10分做法

暴力枚举每个值在A组还是B组，因为ai可以取任意值，就随便瞎取，当搜出的方案只有唯一一种时，显然就是答案，时间复杂度O(n*2^(2^n))

其实这个时候已经可以发现分组有一些神奇的地方，再多想一下就是40分了

 

40分做法

根据暴力，我们有：

n=2时，A={1,4} , B={2,3};

n=3时，A={1,4,6,7} , B={2,3,5,8};

n=4时，A={1,4,6,7,10,11,13,16} , B={2,3,5,8,9,12,14,15}

............

可以发现，第n次的分组，在第n+1次时并没有改变，而新加入的数：

n=3时，新加入A组的数 6=2+22，7=3+22 ，2,3属于B组

      新加入B组的数 5=1+22，8=4+22 ，1,4属于A组

n=4时，新加入A组的数 10=2+23，11=3+23，13=5+23，16=8+23 ，2,3,5,8属于B组

新加入B组的数 9=1+23，12=4+23，14=6+23，15=7+23 ，1,4,6,7 属于A组

不妨大胆猜测，第n次新加入的数，就是另一组中的所有数加上2n-1，递推得出所有数的分组，时间复杂度O(2^n)，其实想到40分100也就出来了

 

100分做法

 

用数学归纳法证明刚刚的结论：

 

对于1 ~ 2n ( n∈N，n>=2 )，1分在A组，2分在B组，并按从小到大排列，若前2k已分组完成，对于新加入的2k+1 ~ 2k+1，若满足，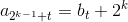

则对于任意 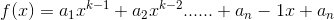，两组和均相等

 

 

 

1.当n=2时，显然，(a1*1 + a2 ) + (a1*4 + a2 ) = (a1*2 + a2 ) + (a1*3 + a2 ),

结论成立;

 

2.假设n=k时结论成立，那么对于n=k+1时，

 

 

 

 

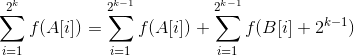
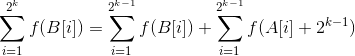
n=k时结论成立，即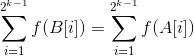

 

 

而将 和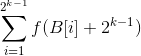拆开，会得到两个系数相等的多项式，k次幂的项完全相等，将剩下的记为g(x)

 

因为n=k时结论成立，且g(x)最高次项不超过k-1次幂，即有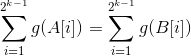，故

成立

由1.2得，此命题成立

那么如何快速判断一个数在A组还是B组？

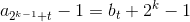，转化为二进制，显然与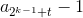中1的个数是不同奇偶的，而与也被分于两组，这意味着判断x在哪一组，即统计x-1在二进制下1的个数，时间复杂度O(qlogx)

可以用lowbit优化，不过加不加都可以过

 

#include<stdio.h>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
char buf[1<<20],*p1,*p2;
#define GC (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?0:*p1++)
inline void R(ll &x)
{
    char t=GC;
    while(t<48||t>57)t=GC;
    for(x=0;t>47&&t<58;t=GC)x=(x<<1)+(x<<3)+t-48;
}
ll n,A[64],q;
int main()
{
//    freopen("wrongans.in","r",stdin);
//    freopen("wrongans.out","w",stdout);
    ll i,j,k,x;
    R(n);R(q);A[0]=1;
    for(i=1;i<=n;i++)A[i]=A[i-1]<<1;
    while(q--)
    {
        k=0;R(x);
        for(i=n;i>=0;i--)if(x>A[i])x-=A[i],k++;
        if(x==2)
        {
            if(k&1)cout<<"X"<<endl;
            else cout<<"Z"<<endl;
        }
        else
        {
            if(k&1)cout<<"Z"<<endl;
            else cout<<"X"<<endl;
        }
    }
}

lowbit优化版

//
#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
long long cnt,n,q;
int main()
{
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    long long x,i;
    cin>>n;
    cin>>q;
    while (q--)
    {
        cin>>x;
        x--;
        cnt=0;
        for (i=x; i; i-=(i&(-i))) cnt++;
        if (cnt%2) cout<<"Z"<<endl;
        else cout<<"X"<<endl;
    }
}

 

C3.部落冲突

题目背景

在一个叫做Travian的世界里，生活着各个大大小小的部落。其中最为强大的是罗马、高卢和日耳曼。他们之间为了争夺资源和土地，进行了无数次的战斗。期间诞生了众多家喻户晓的英雄人物，也留下了许多可歌可泣的动人故事。

其中，在大大小小的部落之间，会有一些道路相连，这些道路是Travian世界里的重要枢纽，简单起见，你可以把这些部落与部落之间相连的道路看作一颗树，可见每条道路对于Travian世界的重要程度。有了这些道路，建筑工人就可以通过这些道路进行友好外交啦。

然而，事情并不会像想象的那样美好，由于资源的匮乏，相邻的部落（由一条道路相连的部落）之间经常会发生大大小小的冲突事件，更有甚者，会升级为部落之间的大型战争。

为了避免误伤，每当两个相邻的部落之间发生大型战争之时，这两个部落间的道路是不允许通行的，对于一些强大的部落，甚至能与多个相邻的部落同时开战，同样的，这些战争地带的道路十分危险，是不可通行的。

天下之势，分久必合，当两个部落经历了不打不相识的苦战之后，他们可以签订停战协议（暂时停战，以后依旧可能再次开战），这样，两个部落之间的道路又会重新恢复为可通行状态，建筑工人们又可以经过此地购买最新的大本营设计图纸来强大自己的部落了。

为了简单起见，我们把各大战争事件按发起的时间顺序依次编号（最先发起的战争编号就为 1，第二次战争编号就为 2，以此类推），当两个部落停战之时，则会直接告诉你这场战争的编号，然后这场战争就载入了史册，不复存在了，当然，这并不会影响到其他战争的编号。

建筑工人十分讨厌战争，因为战争，想从一个部落到另一个部落进行友好交流的建筑工人可能就此白跑一趟。所以，在他们出发之前，都会向你问问能不能到达他们想去的部落。

题目描述

简单起见，你就是要处理下面三件事，所有的事件都是按照时间顺序给出的。

1.（Q p q）从第 p 个部落出发的建筑工人想知道能否到达第 q 个部落了，你要回答的便是（Yes/No），注意大小写

2.（C p q）第 p 个部落与第 q 个部落开战了，保证他们一定是相邻的部落，且目前处于停战（未开战）状态

3.（U x ） 第x 次发生的战争结束了，它将永远的被载入史册，不复存在（保证这个消息不会告诉你多次）

输入格式

第一行两个数 n 和 m， nn 代表了一共有 n 个部落，m 代表了以上三种事件发生的总数

接下来的 n−1 行，每行两个数 p , q，代表了第 p 个部落与第 q 个部落之间有一条道路相连

接下来的 m 行，每行表示一件事，详见题目描述

输出格式

每行一个“Yes”或者“No”，表示从第 p 个部落出发的建筑工人能否到达第q 个部落

输入输出样例
输入 #1 
5 9
1 2
2 3
3 4
4 5
Q 1 4
C 2 1
C 4 3
Q 3 1
Q 1 5
U 1
U 2
C 4 3
Q 3 4
输出 #1 
Yes
No
No
No
输入 #2 
10 10
1 2
1 3
3 4
3 5
1 6
3 7
1 8
2 9
5 10
C 8 1
Q 6 1
C 2 1
Q 2 10
U 1
C 9 2
C 7 3
U 3
Q 6 7
Q 1 10
输出 #2 
Yes
No
No
Yes
输入 #3 
20 20
1 2
1 3
2 4
1 5
1 6
4 7
1 8
2 9
5 10
1 11
2 12
7 13
1 14
1 15
11 16
4 17
3 18
18 19
8 20
Q 13 5
C 14 1
C 16 11
U 1
U 2
C 20 8
Q 7 1
C 7 4
Q 17 17
Q 1 6
C 16 11
C 2 1
Q 16 2
U 3
U 5
U 6
C 2 1
C 6 1
C 13 7
C 11 1
输出 #3 
Yes
Yes
Yes
Yes
No
说明/提示

对于30%的数据 1<=n，m<=6000

对于另30%的数据，保证部落之间的地理关系是一条链，且 i 与 i + 1 之间有一条道路

对于另30%的数据，1<=n，m<=100000

对于100%的数据，1<=n，m<=300000

 

树状数组维护树上差分 O(mlogn）

维护每个点到根节点路径上的的战争个数

#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize(2)  
#pragma GCC optimize(3)
struct node
{
    int to;
    int next;
} edge[700000];
int head[300005],num,VisTime,tot;
int dfn[300005],low[300005],fa[300005][25],dep[300005],C[300005],zz[300005][3];
char ch;
int n,m;
void add(int x,int y)
{
    edge[++num].to=y;
    edge[num].next=head[x];
    head[x]=num;
}
int lowbit(int x)
{
    return x&(-x);
}
void Modify(int x,int k)
{
    for(int i=x;i<=n;i+=lowbit(i))C[i]+=k;
}
int Getsum(int x)
{
    int sum=0;
    for(int i=x; i; i-=lowbit(i))sum+=C[i];
    return sum;
}
void dfs(int x)
{
    dep[x]=dep[fa[x][0]]+1;
    low[x]=dfn[x]=++VisTime;
    int k=ceil(log2(dep[x]));
    for(int i=1; i<=k; i++)
    {
        fa[x][i]=fa[fa[x][i-1]][i-1];
    }
    for(int i=head[x]; i; i=edge[i].next)
    {
        int v=edge[i].to;
        if(v!=fa[x][0])
        {
            fa[v][0]=x;
            dfs(v);
        }
    }
    low[x]=VisTime;
}

int GetLCA(int x,int y)
{
    if(x==y)return x;
    if(dep[x]<dep[y])swap(x,y);
    int k=ceil(log2(dep[x]));
    int s=dep[x]-dep[y];
    for(int i=0; i<=k; i++)if(s&(1<<i))x=fa[x][i];
    if(x==y)return x;
    k=ceil(log2(dep[x]));
    for(int i=k; i>=0; i--)
    {
        if(fa[x][i]!=fa[y][i])
        {
            x=fa[x][i];
            y=fa[y][i];
        }
    }
    return fa[x][0];
}

void Query(int x,int y)
{
    int LCA=GetLCA(x,y);
    int Ans=Getsum(dfn[x])+Getsum(dfn[y])-2*Getsum(dfn[LCA]);
    if(Ans)cout<<"No"<<endl;
    else cout<<"Yes"<<endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    int aa,bb;
    cin>>n>>m;
    for(int i=1; i<n; i++)
    {
        cin>>aa>>bb;
        add(aa,bb);
        add(bb,aa);
    }
    dfs(1);
    for(int i=1; i<=m; i++)
    {
        cin>>ch;
        while(ch!='U'&&ch!='C'&&ch!='Q')cin>>ch;
        if(ch=='Q')
        {
            int a,b;
            cin>>a>>b;
            Query(a,b);
        }
        if(ch=='C') 
        {
            int xx,yy;
            cin>>xx>>yy;
            zz[++tot][0]=xx;
            zz[tot][1]=yy;
            if(dep[xx]<dep[yy])swap(xx,yy);
            Modify(dfn[xx],1);
            if(low[xx]<n)Modify(low[xx]+1,-1);
        }
        if(ch=='U') 
        {
            int ti;
            cin>>ti;
            int x=zz[ti][0],y=zz[ti][1];
            if(dep[x]<dep[y])swap(x,y);
            Modify(dfn[x],-1);
            if(low[x]<n)Modify(low[x]+1,1);
        }
    }
}

 

 

posted @ 2019-10-31 10:54  CXYscxy  阅读(206)  评论(0)  编辑  收藏  举报
Live2D