2019 年 10 月训练赛(10.30晚)

2019 年 10 月训练赛

题目名称	相似围栏	路径异或	路径乘积
程序文件名	fence	pathxor	waymul
输入文件名	fence.in	pathxor.in	waymul.in
输出文件名	fence.out	pathxor.out	waymul.out
每个测试点时限	1 sec	1 sec	4 sec
测试点数目	10	10	10
每个测试点分值	10	10	10
内存限制	256m	256m	512m
题目类型	传统型	传统型	传统型

1. 相似围栏
(fence.pas/c/cpp)
【问题描述】
何老板购置了一套别墅， 该别墅门口有一片花园， 何老板用 n 块高度不同的木板排成一
排， 搭建了围栏。
一天何老板叫了外卖， 正好是刘郃德骑车送递， 刘被拦在围栏之外， 他发现何老板家的
围栏看起来很好看， 很有高级感。 于是刘郃德也买了 n 块高度不同的木板， 打算参照何老板
的方案， 搭建相似的围栏。 所谓“相似” 是指， 刘郃德的相邻两块木板的高度关系与何老板
对应位置的两块木板的高度关系相同。 比如何老板围栏的第 i 块木板的高度大于第 i+1 块，
那么刘郃德围栏的第 i 块木板的高度也必须大于第 i+1 块。
同时， 刘郃德想要相邻两块木板高度差的绝对值之和尽量大。 请你帮他找出最优方案。
【输入格式】
第一行， 一个整数 n
第二行， n 个整数， 依次表示何老板围栏的每块木板的高度。
第三行， n 个整数， 表示刘郃德购买的木板的高度。
【输出格式】
一行， 一个整数， 表示高度差之和的最大值。
【输入输出样例】

样例输入1
4

5 7 4 9

1 2 3 4

样例输出1

7

样例输入2

10
9 5 1 2 6 7 4 18 20 12
10 40 20 30 50 70 80 100 1000 500

样例输出1

3010

【数据范围】
对于 30%的数据： 2 ≤ n ≤ 20
对于 50%的数据： 2 ≤ n ≤ 500
对于 100%的数据： 2 ≤ n ≤ 300000, 1≤木板的高度≤10^9

考察点：观察 贪心 贡献计算
如下图，以第二组样例数据为例，我们观察发现最终答案只跟转折点有关(图 1 的红色点)
比如 9 5 1 的差值和为(9-5)+(5-1)=8=(9-1)
那么我们只需确定转折点即可，如图 2 所示，高处的转折点经可能安排值大的数字
低处的转折点尽可能安排值小的数字，其它数字对答案不产生贡献，可以忽略。

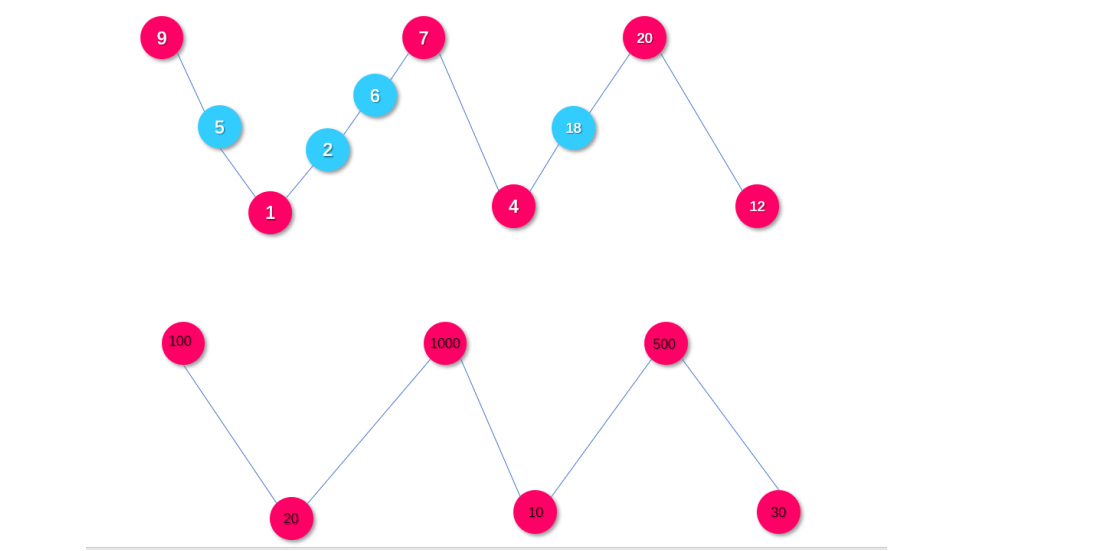
需要注意的是，因为只考虑转折点，而一个转折点有可能之连接对面一个点，也可能连接对
面两个点。对于高处的点，值越大的点，我们希望它连接点越多越好。对于低处的点，值越
小的点，我们希望它连的点越多越好。所以，在安排高处转折点时，值大的安排在中间，值
小的安排在两侧。在安排低处转折点时，值小的安排在中间，值大的安排在两侧。
只需要排序，时间复杂度 O(nlogn)