树上问题专练-----电压

电压

 

C电压

时间限制 : 10000 MS   空间限制 : - KB 

评测说明 : 1s,256m

 

问题描述

 

JOI社的某个实验室中有着复杂的电路。电路由n个节点和m根细长的电阻组成。节点被标号为1~N

每个节点有一个可设定的状态【高电压】或者【低电压】。每个电阻连接两个节点，只有一端是高电压，另一端是低电压的电阻才会有电流流过。两端都是高电压或者低电压的电阻不会有电流流过。

某天，JOI社为了维护电路，选择了一根电阻，为了能让【只有这根电阻上的电流停止流动，其他M-1根电阻中都有电流流过】，需要调节各节点的电压。为了满足这个条件，能选择的电阻共有多少根？

对了，JOI社这个奇妙的电路是用在什么样的发明上的呢？这是公司内的最高机密，除了社长以外谁都不知道哦~

现在给出电路的信息，请你输出电路维护时可以选择使其不流的电阻的个数。

 

输入格式

 

第一行两个空格分隔的正整数N和M，表示电路中有N个节点和M根电阻。
接下来M行，第i行有两个空格分隔的正整数Ai和Bi(1<=Ai<=N,1<=Bi<=N,Ai≠Bi)，表示第i个电阻连接节点Ai和节点Bi。

 

输出格式

 

输出一行一个整数，代表电路维护时可选择的使其不流的电阻个数。

 

样例输入

4 4
1 2
2 3
3 2
4 3

样例输出

2

 

提示

 

 

 

HINT

 

 

可以选择第一根电阻或第四根电阻。

 

2<=N<=10^5

1<=M<=2*10^5

不保证图是连通的，不保证没有重边

 

分析

建一棵DFS树，则特殊边就全部为返祖边 用ji[u]对结点u统计奇环,ou[u]统计偶环 设一条返祖边为 u-> v 若它形成奇环，则ji[u]++,ji[v]--. 则u的子树所有结点的ji之和，即为u -> fa这条边被多少奇环包含 （差分前缀和的思想）（树上差分）

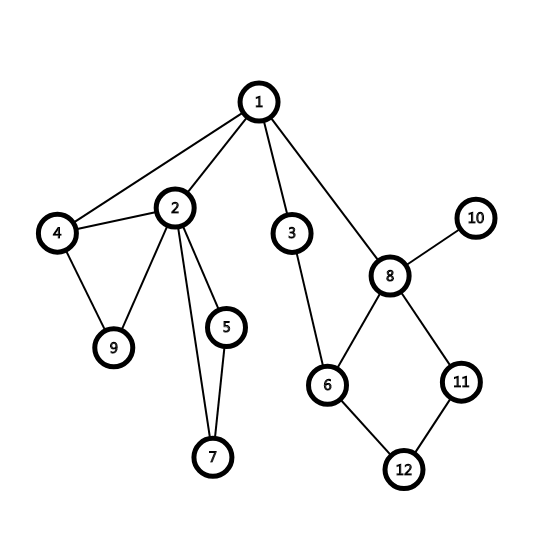
4-->1   ji[4]++, ji[1]--（ ji[4]=1，ji[1]=-1）

7-->2  ji[7]++, ji[2]--（ ji[7]=1，ji[2]=-1）

9-->2  ji[9]++,ji[2]--（ ji[9]=1，ji[2]=-2）

8-->1 ou[8]++,ou[1]--（ ou[8]=1，ou[1]=-1）

12-->6 ou[12]++,ou[6]--（ o[12]=1，ou[1]=-1）

u的子树所有结点的ji之和，即为u -> fa这条边被多少奇环包含

如：u==2

ji[2]+ji[4]+ji[9]+ji[5]+ji[7]=1

则2--1被奇环覆盖了一次（4,2,1）

同理

u==8

ou[8]+ou[10]+ou[11]+ou[12]=2

则8--12被偶环覆盖了2次（8,11,12,6）（8,6,3,1）

奇环的情况可以选的边是环上的边，偶环的情况可以选的边是非环上的边；

而当多个环同时存在的时候，可以选的边是这些环可以选边的交集（无影响）

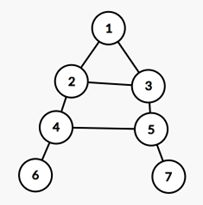
情况1：两个与树边形成奇环的边 一定产生一个偶环(2,3,4,5) 但偶环上的边不可能被所有奇环包含

情况2：两个偶环 本来他们的边就全部不满足条件 不用考虑多生成的新偶环(2,4,7,5)

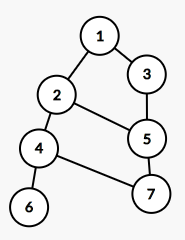
情况3：一个奇环+一个偶环 生成一个奇环(2,5,7,6,4) 这个奇环的树边本来就在原奇环上 无需考虑

唯一非树边会有贡献的情况就是有且仅有一个奇环，此时一定只有一条非树边在奇环内 提供贡献
记录这个点连向父亲的边被几个奇环几个偶环所覆盖；
然后被所有的奇环覆盖又不被任意偶环覆盖的边即是答案；
非树边的情况只有奇环数为1的时候才能选那一条

#include<stdio.h>
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T& x)
{
    char ch=getchar();
    bool sign=true;
    while(!isdigit(ch))
    {
        if(ch=='-')sign=false;
        ch=getchar();
    }
    for(x=0; isdigit(ch); ch=getchar())x=x*10+ch-'0';
    if(!sign)x=-x;
}
struct node
{
    int to;
    int next;
} edge[2000005];
int n,m,fa[200010],head[2000010],num=1,d[200010],ji[200010],ou[200010],sumou,sumji,ans;//ji[u]对结点u统计奇环,ou[u]统计偶环
inline void add(int x,int y)
{
    edge[++num].to=y;
    edge[num].next=head[x];
    head[x]=num;
}
void dfs(int x,int y)
{
    for(int i=head[x]; i; i=edge[i].next)
    {
        if((i^1)!=y)
        {
            int v=edge[i].to;
            if(d[v])//存在返族边
            {
                if(d[v]>d[x]) continue;
                if((d[x]-d[v])&1)//奇数环----对于一条返祖边，如果它连接的两个点的深度差为偶数，说明它在奇环上；否则在偶环上
                    ++ji[x],--ji[v],++sumji;//记录差分（奇环）
                else ++ou[x],--ou[v],++sumou;//记录差分（偶环）
            }
            else
            {
                d[v]=d[x]+1;//访问顺序
                dfs(v,i);//继续向下
                ji[x]+=ji[v];
                ou[x]+=ou[v];
            }
        }
    }
}
int main()
{
    read(n),read(m);
    for(int i=1; i<=m; ++i)
    {
        int x,y;
        read(x),read(y);
        add(x,y),add(y,x);
    }
    for(int i=1; i<=n; ++i)
    {
        if(!d[i])//未讨论过
        {
            d[i]=1;//深度记为一
            dfs(i,0);
            fa[i]=1;
        }
    }
    for(int i=1; i<=n; ++i)
    {
        if(!fa[i]&&ou[i]==sumou&&!ji[i]) ++ans;
        //if(fa[i]&&ji[i]==sumji&&!ou[i]) ans++;
    }
    if(sumou==1) ++ans;//只有一条返祖边在奇环上，将答案+1
    cout<<ans;
    return 0;
}