poj 3608:Bridge Across Islands
| Time Limit: 1000MS | Memory Limit: 65536K | |||
| Total Submissions: 9646 | Accepted: 2834 | Special Judge | ||
Description
Thousands of thousands years ago there was a small kingdom located in the middle of the Pacific Ocean. The territory of the kingdom consists two separated islands. Due to the impact of the ocean current, the shapes of both the islands became convex polygons. The king of the kingdom wanted to establish a bridge to connect the two islands. To minimize the cost, the king asked you, the bishop, to find the minimal distance between the boundaries of the two islands.
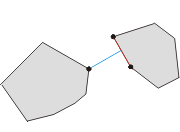
Input
The input consists of several test cases.
Each test case begins with two integers N, M. (3 ≤ N, M ≤ 10000)
Each of the next N lines contains a pair of coordinates, which describes the position of a vertex in one convex polygon.
Each of the next M lines contains a pair of coordinates, which describes the position of a vertex in the other convex polygon.
A line with N = M = 0 indicates the end of input.
The coordinates are within the range [-10000, 10000].
Output
For each test case output the minimal distance. An error within 0.001 is acceptable.
Sample Input
4 4
0.00000 0.00000
0.00000 1.00000
1.00000 1.00000
1.00000 0.00000
2.00000 0.00000
2.00000 1.00000
3.00000 1.00000
3.00000 0.00000
0 0
Sample Output
1.00000
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #include<vector> 9 using namespace std; 10 const double eps=1e-8; 11 const int maxn=10010; 12 int np,nq; 13 double ANS; 14 struct P{ 15 double x,y; 16 friend P operator-(P a,P b){ 17 P t; t.x=a.x-b.x; t.y=a.y-b.y; 18 return t; 19 } 20 friend double operator*(P a,P b){//重载叉乘运算符 21 return a.x*b.y-b.x*a.y; 22 } 23 friend double operator^(P a,P b){//重载点乘运算符 24 return a.x*b.x+a.y*b.y; 25 } 26 }p[maxn],q[maxn]; 27 inline double dis(P a,P b){ 28 return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); 29 } 30 inline double dotcross(P p0,P p1,P p2){//向量p0p1 点乘 向量p0p2 31 P t1=p1-p0,t2=p2-p0; 32 return t1^t2; 33 } 34 inline double difcross(P p0,P p1,P p2){//向量p0p1 叉乘 向量p0p2 35 P t1=p1-p0,t2=p2-p0; 36 return t1*t2; 37 } 38 inline double p2seg(P A,P B,P C){//返回 C到线段 AB的最短距离 39 if(dotcross(A,B,C)<-eps) return dis(A,C); 40 if(dotcross(B,A,C)<-eps) return dis(B,C); 41 return fabs(difcross(A,B,C)/dis(A,B)); 42 } 43 inline double FourP(P A,P B,P C,P D){ 44 double ans1=min(p2seg(A,B,C),p2seg(A,B,D)); 45 double ans2=min(p2seg(C,D,A),p2seg(C,D,B)); 46 return min(ans1,ans2); 47 } 48 inline double solve(P p[],P q[],int np,int nq){ 49 int sp=1,sq=1; 50 for(int i=1;i<=np;i++){ 51 if(p[i].y<p[sp].y) sp=i; 52 } 53 for(int i=1;i<=nq;i++){ 54 if(q[i].y>q[sq].y) sq=i; 55 } 56 p[np+1]=p[1]; q[nq+1]=q[1]; 57 double tmp,ans=1e99; 58 for(int i=1;i<=np;i++){ 59 while( tmp=difcross(p[sp+1],q[sq+1],p[sp])-difcross(p[sp+1],q[sq],p[sp])>eps)//tmp<eps 向量sp,sp+1与向量sq+1,sq平行 60 sq=sq%nq+1; 61 if(tmp<-eps){//两线不平行 62 ans=min(ans,p2seg(p[sp],p[sp+1],q[sq])); 63 } 64 else ans=min(ans,FourP(p[sp],p[sp+1],q[sq],q[sq+1]));//两线平行 65 sp=sp%np+1; 66 } 67 return ans; 68 } 69 int main(){ 70 while(scanf("%d%d",&np,&nq)!=EOF){ 71 if(np==0&&nq==0) break; 72 for(int i=1;i<=np;i++) scanf("%lf%lf",&p[i].x,&p[i].y); 73 for(int i=1;i<=nq;i++) scanf("%lf%lf",&q[i].x,&q[i].y); 74 ANS=solve(p,q,np,nq); 75 ANS=min(ANS,solve(q,p,nq,np)); 76 printf("%.5lf\n",ANS); 77 } 78 return 0; 79 }




