Tarjan 求强连通分量
首先介绍一下什么是(有向图)强连通分量——
在有向图G中,如果两个顶点间至少存在一条路径,称两个顶点强连通。如果有向图G的每两个顶点都强连通,则称G是一个强连通图。非强连通图有向图的极大强连通子图,成为强连通分量。
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达,{5},{6}也分别是两个强连通分量。
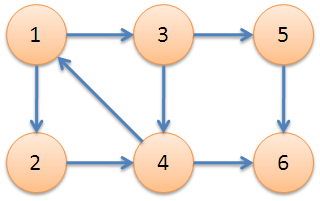
tarjan算法是利用dfs依次遍历相连的点,每到达一个点,就记录下到达该点的次序(即程序中的dfn数组),与一个待更新的最早次序,每个点的最早次序是指与其同处一个环的点的最小次序(例如:依次到达点2、4、6、7、3,其到达次序分别为1、2、3、4、5,若此五点在一个环中,则其最小次序均为1。这个在程序中用low数组维护),之后将这个点压入一个栈(在后来同处一个环的会一起弹出)。
显然同处一个环的除第一个被遍历的点的low是小于dfn的,所以说当将遇到dfn与low相等的点就将与它上面的点(还记得那个存在感极低的栈吗?)一起弹出,弹出的一系列的点就在一个环里。如果一个点不与其他点构成环,显然会只弹出这一单点。
更新low时注意要分类讨论一下,其他就没什么了。
下面是个输出同处一个环的点的程序。
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=5005; 4 int N,M; 5 int stac[maxn],top=0;//Tarjan算法中的栈 6 bool instac[maxn];//检查是否在栈中 7 int dfn[maxn];//深度优先搜索访问次序 8 int low[maxn];//能追溯到的最早的次序 9 int tot=0;//有向图强连通分量个数 10 int index=0;//索引号 11 vector<int>to[maxn]; 12 vector<int> kin[maxn];//获得强连通分量结果 13 int inkin[maxn];//记录每个点在第几号强连通分量里 14 15 inline void tarjan(int x){ 16 dfn[x]=low[x]=index++; 17 stac[++top]=x; 18 instac[x]=true; 19 for(int i=0;i<to[x].size();i++){ 20 int y=to[x][i]; 21 if(dfn[y]==-1){ 22 tarjan(y); 23 low[x]=min(low[x],low[y]); 24 } 25 else if(instac[y]!=0){ 26 low[x]=min(low[x],dfn[y]); 27 } 28 } 29 if(dfn[x]==low[x]){ 30 tot++; 31 int y; 32 do{ 33 y=stac[top--]; 34 instac[y]=false; 35 kin[tot].push_back(y); 36 inkin[y]=tot; 37 }while(y!=x); 38 } 39 } 40 int main(){ 41 scanf("%d%d",&N,&M); 42 for(int i=1;i<=M;i++){ 43 int u,v; 44 scanf("%d%d",&u,&v); 45 to[u].push_back(v); 46 } 47 memset(dfn,-1,sizeof(dfn)); 48 for(int i=1;i<=N;i++){ 49 if(dfn[i]==-1) tarjan(i); 50 } 51 for(int i=1;i<=N;i++){//输出分组 52 cout<<inkin[i]<<endl; 53 } 54 return 0; 55 }



