剑指offer一刷：搜索与回溯算法

剑指 Offer 32 - I. 从上到下打印二叉树

难度：中等

方法一：层序遍历 BFS

题目要求的二叉树的从上至下打印（即按层打印），又称为二叉树的广度优先搜索（BFS）。

BFS 通常借助队列的先入先出特性来实现。

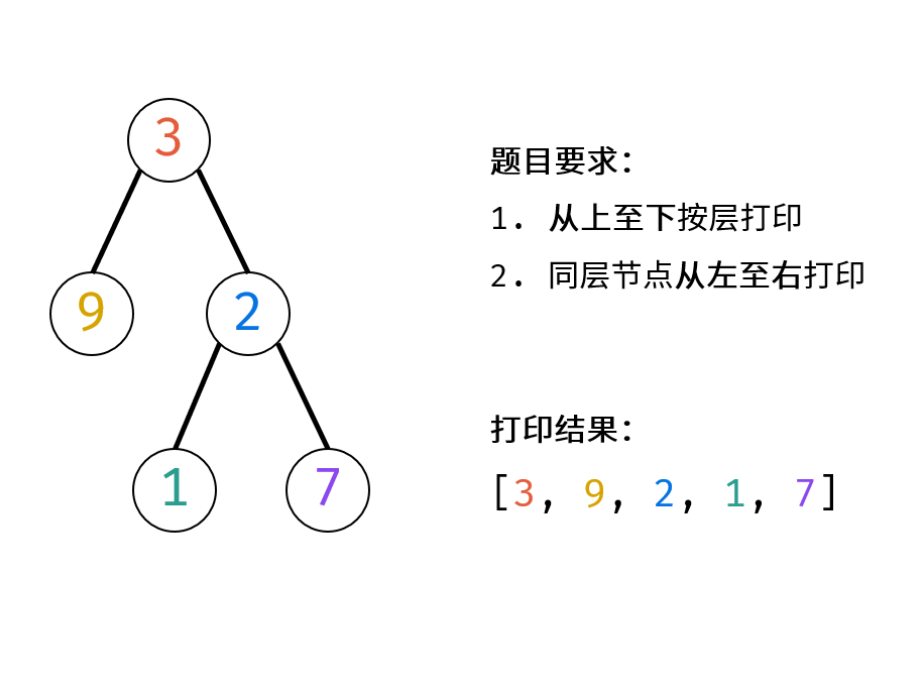
算法流程：

特例处理：当树的根节点为空，则直接返回空列表 []；
初始化：打印结果列表 res = []，包含根节点的队列 queue = [root]；
BFS 循环：当队列 queue 为空时跳出；
1. 出队：队首元素出队，记为 node；
2. 打印：将 node.val 添加至列表 tmp 尾部；
3. 添加子节点：若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 queue；
返回值：返回打印结果列表 res 即可。

class Solution {
    public int[] levelOrder(TreeNode root) {
        if(root == null) return new int[0];
        Queue<TreeNode> queue = new LinkedList<>(){{ add(root); }};
        ArrayList<Integer> ans = new ArrayList<>();
        while(!queue.isEmpty()) {
            TreeNode node = queue.poll();
            ans.add(node.val);
            if(node.left != null) queue.add(node.left);
            if(node.right != null) queue.add(node.right);
        }
        int[] res = new int[ans.size()];
        for(int i = 0; i < ans.size(); i++)
            res[i] = ans.get(i);
        return res;
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/9ab39g/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

剑指 Offer 32 - II. 从上到下打印二叉树 II

难度：简单

方法一：层序遍历 BFS

在 I 的基础上，将本层全部节点打印到一行，并将下一层全部节点加入队列，以此类推，即可分为多行打印。

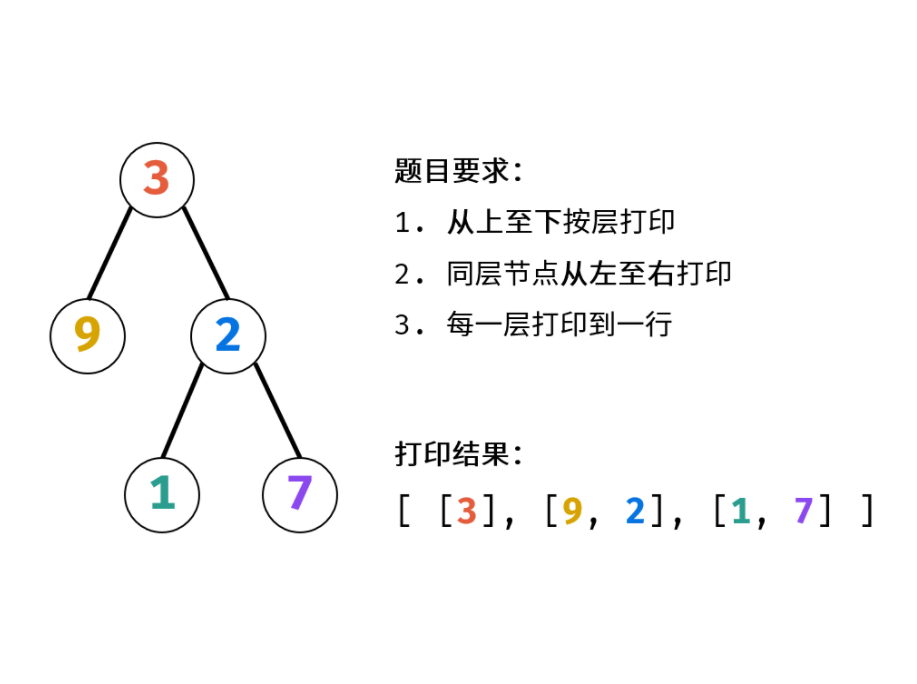
算法流程：

特例处理：当根节点为空，则返回空列表 []；
初始化：打印结果列表 res = []，包含根节点的队列 queue = [root]；
BFS 循环：当队列 queue 为空时跳出；
1. 新建一个临时列表 tmp，用于存储当前层打印结果；
2. 当前层打印循环：循环次数为当前层节点数（即队列 queue 长度）；
  1. 出队：队首元素出队，记为 node；
  2. 打印：将 node.val 添加至 tmp 尾部；
  3. 添加子节点：若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 queue；
3. 将当前层结果 tmp 添加入 res。
返回值：返回打印结果列表 res 即可。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) queue.add(root);
        while(!queue.isEmpty()) {
            List<Integer> tmp = new ArrayList<>();
            for(int i = queue.size(); i > 0; i--) {
                TreeNode node = queue.poll();
                tmp.add(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            res.add(tmp);
        }
        return res;
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5v22om/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

其中的 int i = queue.size(); 用的很妙，学习学习。

剑指 Offer 32 - III. 从上到下打印二叉树 III

难度：中等

方法一：层序遍历 + 双端队列

算法流程：

特例处理：当树的根节点为空，则直接返回空列表 []；
初始化：打印结果空列表 res，包含根节点的双端队列 deque；
BFS 循环：当 deque 为空时跳出；
1. 新建列表 tmp，用于临时存储当前层打印结果；
2. 当前层打印循环：循环次数为当前层节点数（即 deque 长度）；
  1. 出队：队首元素出队，记为 node；
  2. 打印：若为奇数层，将 node.val 添加至 tmp 尾部；否则，添加至 tmp 头部；
  3. 添加子节点：若 node 的左（右）子节点不为空，则加入 deque；
3. 将当前层结果 tmp 转化为 list 并添加入 res；
返回值：返回打印结果列表 res 即可；

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) queue.add(root);
        while(!queue.isEmpty()) {
            LinkedList<Integer> tmp = new LinkedList<>();
            for(int i = queue.size(); i > 0; i--) {
                TreeNode node = queue.poll();
                if(res.size() % 2 == 0) tmp.addLast(node.val);
                else tmp.addFirst(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            res.add(tmp);
        }
        return res;
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5vve57/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

方法二：层序遍历 + 双端队列（奇偶逻辑分离）

方法一代码简短、容易实现；但需要判断每个节点的所在层奇偶性，即冗余了次判断。
通过将奇偶层逻辑拆分，可以消除冗余的判断。

算法流程：

BFS 循环：循环打印奇 / 偶数层，当 deque 为空时跳出；
1. 打印奇数层：从左向右打印，先左后右加入下层节点；
2. 若 deque 为空，说明向下无偶数层，则跳出；
3. 打印偶数层：从右向左打印，先右后左加入下层节点；

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Deque<TreeNode> deque = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) deque.add(root);
        while(!deque.isEmpty()) {
            // 打印奇数层
            List<Integer> tmp = new ArrayList<>();
            for(int i = deque.size(); i > 0; i--) {
                // 从左向右打印
                TreeNode node = deque.removeFirst();
                tmp.add(node.val);
                // 先左后右加入下层节点
                if(node.left != null) deque.addLast(node.left);
                if(node.right != null) deque.addLast(node.right);
            }
            res.add(tmp);
            if(deque.isEmpty()) break; // 若为空则提前跳出
            // 打印偶数层
            tmp = new ArrayList<>();
            for(int i = deque.size(); i > 0; i--) {
                // 从右向左打印
                TreeNode node = deque.removeLast();
                tmp.add(node.val);
                // 先右后左加入下层节点
                if(node.right != null) deque.addFirst(node.right);
                if(node.left != null) deque.addFirst(node.left);
            }
            res.add(tmp);
        }
        return res;
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5vve57/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

方法三：层序遍历 + 倒序

偶数层倒序：若 res 的长度为奇数，说明当前是偶数层，则对 tmp 执行倒序操作。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) queue.add(root);
        while(!queue.isEmpty()) {
            List<Integer> tmp = new ArrayList<>();
            for(int i = queue.size(); i > 0; i--) {
                TreeNode node = queue.poll();
                tmp.add(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            if(res.size() % 2 == 1) Collections.reverse(tmp);
            res.add(tmp);
        }
        return res;
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5vve57/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

剑指 Offer 26. 树的子结构

难度：中等

方法一：先序遍历 + 包含判断

若树 B 是树 A 的子结构，则子结构的根节点可能为树 A 的任意一个节点。因此，判断树 B 是否是树 A 的子结构，需完成以下两步工作：

先序遍历树 A 中的每个节点 n_A；（对应函数 isSubStructure(A, B) ）
判断树 A 中以 n_A为根节点的子树是否包含树 B。（对应函数 recur(A, B) ）

class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        return (A != null && B != null) && (recur(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B));
    }
    boolean recur(TreeNode A, TreeNode B) {
        if(B == null) return true;
        if(A == null || A.val != B.val) return false;
        return recur(A.left, B.left) && recur(A.right, B.right);
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5dsbng/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(MN)，空间复杂度：O(M)，其中分别为树 A 和树 B 的节点数量。

剑指 Offer 27. 二叉树的镜像

难度：简单

（注意是对原树镜像，不是输出一个新的镜像，一开始做错了）

方法一：递归法

class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if(root == null) return null;
        TreeNode tmp = root.left;
        root.left = mirrorTree(root.right);
        root.right = mirrorTree(tmp);
        return root;
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/59slxe/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

方法二：辅助栈（或队列）

算法流程：

特例处理：当 root 为空时，直接返回 null；
初始化：栈（或队列），本文用栈，并加入根节点 root。
循环交换：当栈 stack 为空时跳出；
1. 出栈：记为 node；
2. 添加子节点：将 node 左和右子节点入栈；
3. 交换：交换 node 的左 / 右子节点。
返回值：返回根节点 root。

class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if(root == null) return null;
        Stack<TreeNode> stack = new Stack<>() {{ add(root); }};
        while(!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if(node.left != null) stack.add(node.left);
            if(node.right != null) stack.add(node.right);
            TreeNode tmp = node.left;
            node.left = node.right;
            node.right = tmp;
        }
        return root;
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/59slxe/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

剑指 Offer 28. 对称的二叉树

难度：简单

方法一：递归法

对称二叉树定义：对于树中任意两个对称节点 L 和 R，一定有：

L.val = R.val：即此两对称节点值相等。
L.left.val = R.right.val：即 L 的左子节点和 R 的右子节点对称；
L.right.val = R.left.val：即 L 的右子节点和 R 的左子节点对称。

根据以上规律，考虑从顶至底递归，判断每对左右节点是否对称，从而判断树是否为对称二叉树。

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return root == null || recur(root.left, root.right);
    }
    boolean recur(TreeNode L, TreeNode R) {
        if(L == null && R == null) return true;
        if(L == null || R == null || L.val != R.val) return false;
        return recur(L.left, R.right) && recur(L.right, R.left);
    }
}

作者：Krahets
链接：https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/5d1zmj/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

剑指 Offer 12. 矩阵中的路径

难度：中等

方法一：深度优先搜索（DFS）+ 剪枝

本问题是典型的矩阵搜索问题，可使用深度优先搜索（DFS）+ 剪枝解决。

深度优先搜索：可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
剪枝：在搜索中，遇到这条路不可能和目标字符串匹配成功的情况（例如：此矩阵元素和目标字符不同、此元素已被访问），则应立即返回，称之为可行性剪枝。

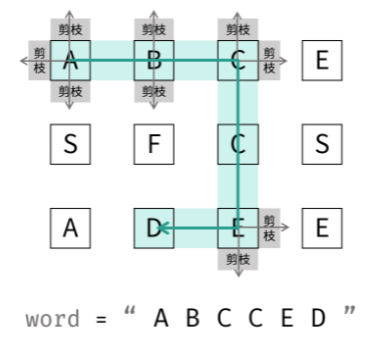
DFS 解析：

递归参数：当前元素在矩阵 board 中的行列索引 i 和 j，当前目标字符在 word 中的索引 k。
终止条件：
1. 返回 false：(1) 行或列索引越界或 (2) 当前矩阵元素与目标字符不同或 (3) 当前矩阵元素已访问过（ (3) 可合并至 (2) ）。
2. 返回 true：k = len(word) - 1，即字符串 word 已全部匹配。
递推工作：
1. 标记当前矩阵元素：将 board[i][j] 修改为空字符 ''，代表此元素已访问过，防止之后搜索时重复访问。
2. 搜索下一单元格：朝当前元素的上、下、左、右四个方向开启下层递归，使用或连接（代表只需找到一条可行路径就直接返回，不再做后续 DFS），并记录结果至 res。
3. 还原当前矩阵元素：将 board[i][j] 元素还原至初始值，即 word[k]。
返回值：返回布尔量 res，代表是否搜索到目标字符串。

使用空字符（'\0'）做标记是为了防止标记字符与矩阵原有字符重复。当存在重复时，此算法会将矩阵原有字符认作标记字符，从而出现错误。

class Solution {
    public boolean exist(char[][] board, String word) {
        char[] words = word.toCharArray();
        for(int i = 0; i < board.length; i++) {
            for(int j = 0; j < board[0].length; j++) {
                if(dfs(board, words, i, j, 0)) return true;
            }
        }
        return false;
    }
    boolean dfs(char[][] board, char[] word, int i, int j, int k) {
        if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k]) return false;
        if(k == word.length - 1) return true;
        board[i][j] = '\0';
        boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) || 
                      dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);
        board[i][j] = word[k];
        return res;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/58d5vh/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(3^KMN)（方案数 3^K，即舍弃上个字符的方向后剩下 3 个方向，矩阵中共有 MN 个起点），空间复杂度：O(K)（递归深度）。

剑指 Offer 13. 机器人的运动范围

难度：中等

本题与矩阵中的路径类似，是典型的搜索 & 回溯问题。在介绍回溯算法算法前，为提升计算效率，首先讲述两项前置工作：数位之和计算、可达解分析。

数位之和计算：

由于机器人每次只能移动一格（即只能从 x 运动至 x±1），因此每次只需计算 x 到 x±1 的数位和增量。本题说明 1 ≤ n, m ≤ 100，以下公式仅在此范围适用。

数位和增量公式：设 x 的数位和为 s_x，x+1 的数位和为 s_x+1；

当 (x + 1) % 10 = 0 时：s_x+1 = s_x - 8，例如 19, 20 的数位和分别为 10, 2；
当 (x + 1) % 10 ≠ 0 时：s_x+1 = s_x + 1，例如 1, 2 的数位和分别为 1, 2。

以下代码为增量公式的三元表达式写法，将整合入最终代码中。

(x + 1) % 10 != 0 ? s_x + 1 : s_x - 8;

可达解分析：

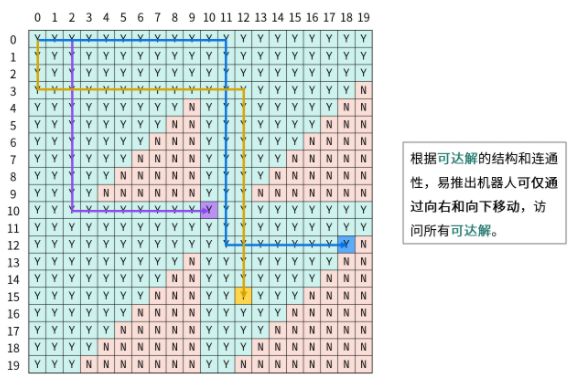
根据数位和增量公式得知，数位和每逢进位突变一次。根据此特点，矩阵中满足数位和的解构成的几何形状形如多个等腰直角三角形，每个三角形的直角顶点位于 0, 10, 20, ... 等数位和突变的矩阵索引处。

三角形内的解虽然都满足数位和要求，但由于机器人每步只能走一个单元格，而三角形间不一定是连通的，因此机器人不一定能到达，称之为不可达解；同理，可到达的解称为可达解（本题求此解）。

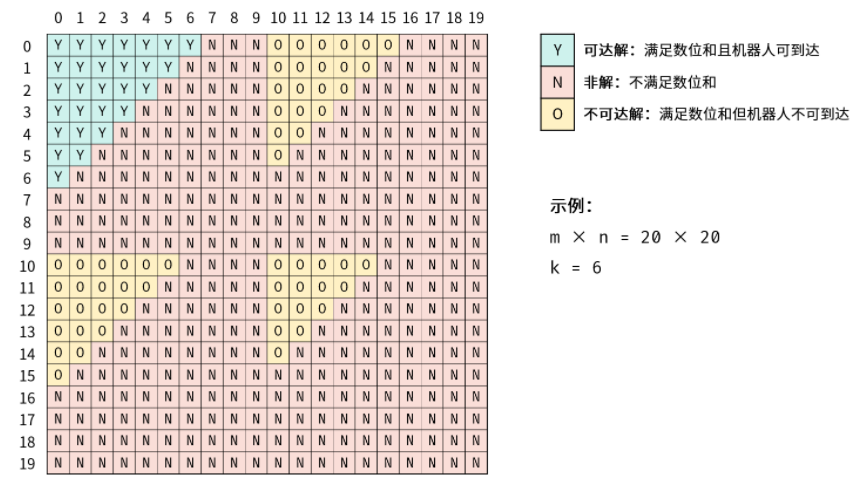
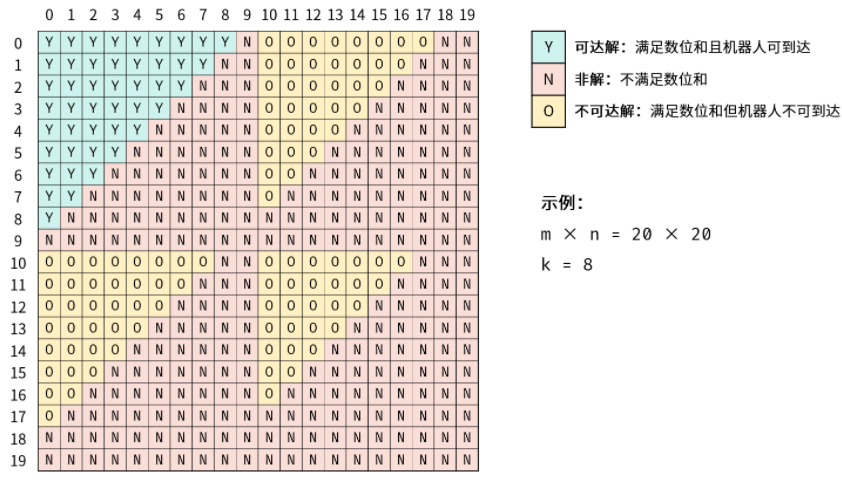
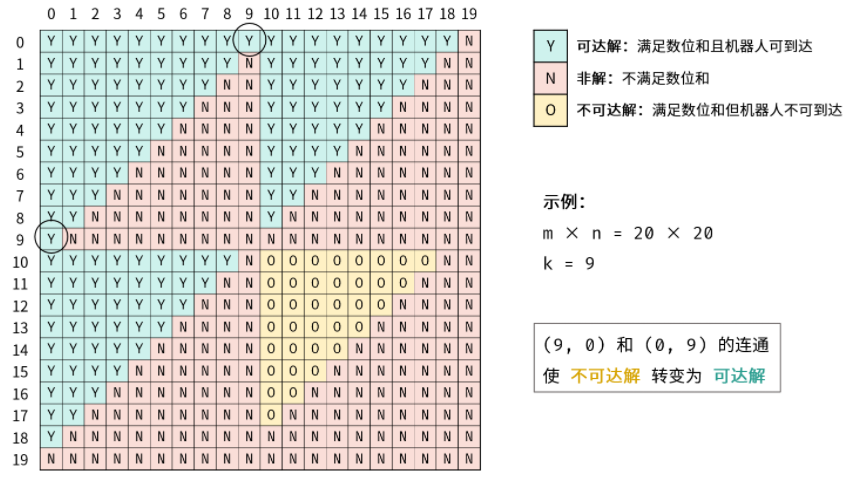
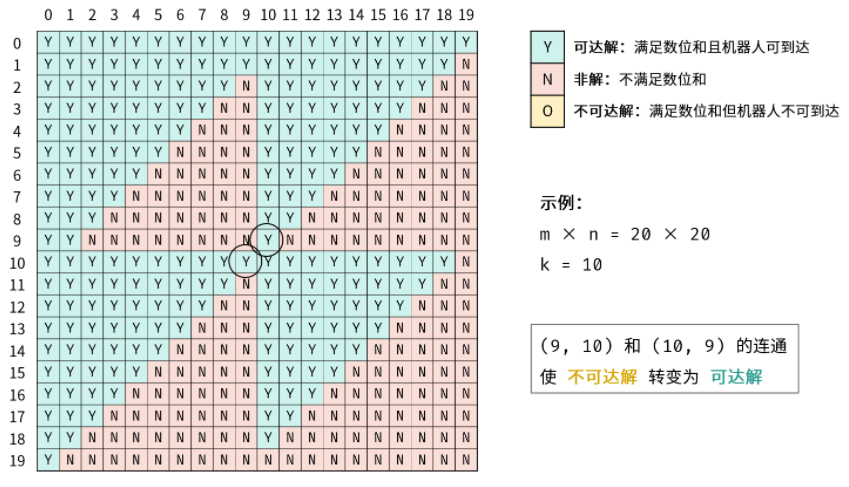
根据可达解的结构和连通性，易推出机器人可仅通过向右和向下移动，访问所有可达解。

方法一：深度优先遍历 DFS

算法解析：

递归参数：当前元素在矩阵中的行列索引 i 和 j，两者的数位和 si, sj。
终止条件：当 ① 行列索引越界或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过时，返回 0，代表不计入可达解。
递推工作：
1. 标记当前单元格：将索引 (i, j) 存入 Set visited 中，代表此单元格已被访问过。
2. 搜索下一单元格：计算当前元素的下、右两个方向元素的数位和，并开启下层递归。
回溯返回值：返回 1 + 右方搜索的可达解总数 + 下方搜索的可达解总数，代表从本单元格递归搜索的可达解总数。

class Solution {
    int m, n, k;
    boolean[][] visited;
    public int movingCount(int m, int n, int k) {
        this.m = m; this.n = n; this.k = k;
        this.visited = new boolean[m][n];
        return dfs(0, 0, 0, 0);
    }
    public int dfs(int i, int j, int si, int sj) {
        if(i >= m || j >= n || k < si + sj || visited[i][j]) return 0;
        visited[i][j] = true;
        return 1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj) + dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8);
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/9hka9c/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(MN)，空间复杂度：O(MN)。

方法二：广度优先遍历 BFS

BFS/DFS：两者目标都是遍历整个矩阵，不同点在于搜索顺序不同。DFS 是朝一个方向走到底，再回退，以此类推；BFS 则是按照“平推”的方式向前搜索。
BFS 实现：通常利用队列实现广度优先遍历。

算法解析：

初始化：将机器人初始点 (0, 0) 加入队列 queue；
迭代终止条件：queue 为空。代表已遍历完所有可达解。
迭代工作：
1. 单元格出队：将队首单元格的索引、数位和弹出，作为当前搜索单元格。
2. 判断是否跳过：若 ① 行列索引越界或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过时，执行 continue。
3. 标记当前单元格：将单元格索引 (i, j) 存入 Set visited 中，代表此单元格已被访问过。
4. 单元格入队：将当前元素的下方、右方单元格的索引、数位和加入 queue。
返回值：Set visited 的长度 len(visited)，即可达解的数量。

class Solution {
    public int movingCount(int m, int n, int k) {
        boolean[][] visited = new boolean[m][n];
        int res = 0;
        Queue<int[]> queue= new LinkedList<int[]>();
        queue.add(new int[] { 0, 0, 0, 0 });
        while(queue.size() > 0) {
            int[] x = queue.poll();
            int i = x[0], j = x[1], si = x[2], sj = x[3];
            if(i >= m || j >= n || k < si + sj || visited[i][j]) continue;
            visited[i][j] = true;
            res++;
            queue.add(new int[] { i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj });
            queue.add(new int[] { i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8 });
        }
        return res;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/9hka9c/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(MN)，空间复杂度：O(MN)。

剑指 Offer 34. 二叉树中和为某一值的路径

难度：中等

本题是典型的二叉树方案搜索问题，使用回溯法解决，其包含先序遍历 + 路径记录两部分。

先序遍历：按照“根、左、右”的顺序，遍历树的所有节点。
路径记录：在先序遍历中，记录从根节点到当前节点的路径。当路径满足 ① 根节点到叶节点形成的路径且 ② 各节点值的和等于目标值 sum 时，将此路径加入结果列表。

算法流程：

pathSum(root, sum) 函数：

初始化：结果列表 res，路径列表 path。
返回值：返回 res 即可。

recur(root, tar) 函数：

递推参数：当前节点 root，当前目标值 tar。
终止条件：若节点 root 为空，则直接返回。
递推工作：
1. 路径更新：将当前节点值 root.val 加入路径 path。
2. 目标值更新：tar = tar - root.val（即目标值 tar 从 sum 减至 0）。
3. 路径记录：当 ① root 为叶节点且 ② 路径和等于目标值，则将此路径 path 加入 res。
4. 先序遍历：递归左 / 右子节点。
5. 路径恢复：向上回溯前，需要将当前节点从路径 path 中删除，即执行 path.pop()。

注意，应当拷贝一个 path 对象并加入到 res。

此外，因为节点值可能是负数，所以拥有无限可能，不好剪枝(⊙o⊙)…

class Solution {
    LinkedList<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        recur(root, sum);
        return res;
    }
    void recur(TreeNode root, int tar) {
        if(root == null) return;
        path.add(root.val);
        tar -= root.val;
        if(tar == 0 && root.left == null && root.right == null)
            res.add(new LinkedList(path));
        recur(root.left, tar);
        recur(root.right, tar);
        path.removeLast();
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/5dc8rr/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)（最差情况退化成链表）。

剑指 Offer 36. 二叉搜索树与双向链表

难度：中等

根据性质：二叉搜索树的中序遍历为递增序列。

考虑使用中序遍历访问树的各节点 cur；并在访问每个节点时构建 cur 和前驱节点 pre 的引用指向；中序遍历完成后，最后构建头节点和尾节点的引用指向即可。

算法流程：

dfs(cur)：递归法中序遍历；

终止条件：当节点 cur 为空，代表越过叶节点，直接返回；
递归左子树，即 dfs(cur.left)；
构建链表：
1. 当 pre 为空时：代表正在访问链表头节点，记为 head；
2. 当 pre 不为空时：修改双向节点引用，即 pre.right = cur， cur.left = pre；
3. 保存 cur：更新 pre = cur，即节点 cur 是后继节点的 pre；
递归右子树，即 dfs(cur.right)；

treeToDoublyList(root)：

特例处理：若节点 root 为空，则直接返回；
初始化：空节点 pre；
转化为双向链表：调用 dfs(root)；
构建循环链表：中序遍历完成后，head 指向头节点， pre 指向尾节点，因此修改 head 和 pre 的双向节点引用即可；
返回值：返回链表的头节点 head 即可；

class Solution {
    Node pre, head;
    public Node treeToDoublyList(Node root) {
        if(root == null) return null;
        dfs(root);
        head.left = pre;
        pre.right = head;
        return head;
    }
    void dfs(Node cur) {
        if(cur == null) return;
        dfs(cur.left);
        if(pre != null) pre.right = cur;
        else head = cur;
        cur.left = pre;
        pre = cur;
        dfs(cur.right);
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/5dj09d/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)（最差情况退化成链表）。

剑指 Offer 54. 二叉搜索树的第 k 大节点

难度：简单

根据性质：二叉搜索树的中序遍历为递增序列，易得二叉搜索树的中序遍历倒序为递减序列。

为求第 k 个节点，需要实现以下三项工作：

递归遍历时计数，统计当前节点的序号；
递归到第 k 个节点时，应记录结果 res；
记录结果后，后续的遍历即失去意义，应提前终止（即返回）；

递归解析：

终止条件：当节点 root 为空（越过叶节点），则直接返回；
递归右子树：即 dfs(root.right)；
递推工作：
1. 提前返回：若 k = 0，代表已找到目标节点，无需继续遍历，因此直接返回；
2. 统计序号：执行 k = k - 1（即从 k 减至 0）；
3. 记录结果：若 k = 0，代表当前节点为第 k 大的节点，因此记录 res = root.val；
递归左子树：即 dfs(root.left)；

class Solution {
    int res, k;
    public int kthLargest(TreeNode root, int k) {
        this.k = k;
        dfs(root);
        return res;
    }
    void dfs(TreeNode root) {
        if(root == null) return;
        dfs(root.right);
        if(k == 0) return;
        if(--k == 0) res = root.val;
        dfs(root.left);
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/580cam/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

剑指 Offer 55 - I. 二叉树的深度

难度：简单

方法一：后序遍历（DFS）

显然，此树的深度等于左子树的深度与右子树的深度中的最大值 。

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/9hz9xe/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)（最差情况下（当树退化为链表时），递归深度可达到）。

方法二：层序遍历（BFS）

树的层序遍历 / 广度优先搜索往往利用队列实现。
关键点：每遍历一层，则计数器，直到遍历完成，则可得到树的深度。

算法解析：

特例处理：当 root 为空，直接返回深度 0。
初始化：队列 queue（加入根节点 root），计数器 res = 0。
循环遍历：当 queue 为空时跳出。
1. 初始化一个空列表 tmp，用于临时存储下一层节点；
2. 遍历队列：遍历 queue 中的各节点 node，并将其左子节点和右子节点加入 tmp；
3. 更新队列：执行 queue = tmp，将下一层节点赋值给 queue；
4. 统计层数：执行 res += 1，代表层数加 1；
返回值：返回 res 即可。

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        List<TreeNode> queue = new LinkedList<>() {{ add(root); }}, tmp;
        int res = 0;
        while(!queue.isEmpty()) {
            tmp = new LinkedList<>();
            for(TreeNode node : queue) {
                if(node.left != null) tmp.add(node.left);
                if(node.right != null) tmp.add(node.right);
            }
            queue = tmp;
            res++;
        }
        return res;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/9hz9xe/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)（最差情况下（当树平衡时），队列 queue 同时存储个节点）。

剑指 Offer 55 - II. 平衡二叉树

难度：简单

方法一：后序遍历 + 剪枝（从底至顶）

思路是对二叉树做后序遍历，从底至顶返回子树深度，若判定某子树不是平衡树则“剪枝”，直接向上返回。

算法流程：

recur(root) 函数：

返回值：
1. 当节点 root 左 / 右子树的深度差 ≤ 1：则返回当前子树的深度，即节点 root 的左 / 右子树的深度最大值 +1（max(left, right) + 1）；
2. 当节点 root 左 / 右子树的深度差 > 1：则返回 -1，代表此子树不是平衡树。
终止条件：
1. 当 root 为空：说明越过叶节点，因此返回高度 0；
2. 当左（右）子树深度为 -1：代表此树的左（右）子树不是平衡树，因此剪枝，直接返回 -1；

isBalanced(root) 函数：

返回值：若 recur(root) != -1，则说明此树平衡，返回 true；否则返回 false。

class Solution {
    public boolean isBalanced(TreeNode root) {
        return recur(root) != -1;
    }

    private int recur(TreeNode root) {
        if (root == null) return 0;
        int left = recur(root.left);
        if(left == -1) return -1;
        int right = recur(root.right);
        if(right == -1) return -1;
        return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/9hscjv/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)（退化成链表）。

注意：精髓在于把返回值 -1 等价于非平衡二叉树，这样就不需要构造一个 ReturnType 来保存是否为平衡二叉树和深度两个值了。

方法二：先序遍历 + 判断深度（从顶至底）

时间复杂度为 O(NlogN），省略。

具体见剑指 Offer 55 - II 题目解析

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

难度：简单

最近公共祖先的定义：设节点 root 为节点 p、q 的某公共祖先，若其左子节点 root.left 和右子节点 root.right 都不是 p、q 的公共祖先，则称 root 是 “最近的公共祖先”。

根据以上定义，若 root 是 p、q 的最近公共祖先，则只可能为以下情况之一：

p 和 q 在 root 的子树中，且分列 root 的异侧（即分别在左、右子树中）；
p = root，且 q 在 root 的左或右子树中；
q = root，且 p 在 root 的左或右子树中；

本题给定了两个重要条件：① 树为二叉搜索树，② 树的所有节点的值都是唯一的。根据以上条件，可方便地判断 p、q 与 root 的子树关系，即：

若 root.val < p.val，则 p 在 root 右子树中；
若 root.val > p.val，则 p 在 root 左子树中；
若 root.val = p.val，则 p 和 root 指向同一节点；

方法一：迭代

循环搜索：当节点 root 为空时跳出；
1. 当 p、q 都在 root 的右子树中，则遍历至 root.right；
2. 否则，当 p、q 都在 root 的左子树中，则遍历至 root.left；
3. 否则，说明找到了最近公共祖先，跳出；
返回值：最近公共祖先 root；

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while(root != null) {
            if(root.val < p.val && root.val < q.val) // p,q 都在 root 的右子树中
                root = root.right; // 遍历至右子节点
            else if(root.val > p.val && root.val > q.val) // p,q 都在 root 的左子树中
                root = root.left; // 遍历至左子节点
            else break;
        }
        return root;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/5793vc/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)（退化为链表），空间复杂度：O(1)。

代码优化：若可保证，则在循环中可减少判断条件，提升计算效率。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(p.val > q.val) { // 保证 p.val < q.val
            TreeNode tmp = p;
            p = q;
            q = tmp;
        }
        while(root != null) {
            if(root.val < p.val) // p,q 都在 root 的右子树中
                root = root.right; // 遍历至右子节点
            else if(root.val > q.val) // p,q 都在 root 的左子树中
                root = root.left; // 遍历至左子节点
            else break;
        }
        return root;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/5793vc/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

方法二：递归

递推工作：
1. 当 p、q 都在 root 的右子树中，则开启递归 root.right 并返回；
2. 否则，当 p、q 都在 root 的左子树中，则开启递归 root.left 并返回；
返回值：最近公共祖先 root；

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root.val < p.val && root.val < q.val)
            return lowestCommonAncestor(root.right, p, q);
        if(root.val > p.val && root.val > q.val)
            return lowestCommonAncestor(root.left, p, q);
        return root;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/5793vc/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

剑指 Offer 68 - II. 二叉树的最近公共祖先

难度：简单

递归解析：

终止条件：
1. 当越过叶节点，则直接返回 null；
2. 当 root 等于 p、q，则直接返回 root；（特别说明一下，这里就包含了“p 或 q 本身就是最近公共祖先”这种情况）
递推工作：
1. 开启递归左子节点，返回值记为 left；
2. 开启递归右子节点，返回值记为 right；
返回值：根据 left 和 right，可展开为四种情况；
1. 当 left 和 right 同时为空：说明 root 的左 / 右子树中都不包含 p、q，返回 null；
2. 当 left 和 right 同时不为空：说明 p、q 分列在 root 的异侧（分别在左 / 右子树），因此 root 为最近公共祖先，返回 root；
3. 当 left 为空，right 不为空：p、q 都不在 root 的左子树中，直接返回 right。具体可分为两种情况：
  1. p、q 其中一个在 root 的右子树中，此时 right 指向 p（假设为 p）；
  2. p、q 两节点都在 root 的右子树中，此时的 right 指向最近公共祖先节点；
4. 当 left 不为空，right 为空：与情况 3. 同理；

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || root == p || root == q) return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
//        if(left == null && right == null) return null; // 1.   可合并到3.和4.中
        if(left == null) return right; // 3.
        if(right == null) return left; // 4.
        return root; // 2. if(left != null and right != null)
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/57o72e/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N)，空间复杂度：O(N)。

剑指 Offer 37. 序列化二叉树

难度：困难

序列化使用层序遍历实现。反序列化通过递推公式反推各节点在序列中的索引，进而实现。

序列化 Serialize：

借助队列，对二叉树做层序遍历，并将越过叶节点的 null 也打印出来。

算法流程：

特例处理：若 root 为空，则直接返回空列表 "[]"；
初始化：队列 queue（包含根节点 root）；序列化列表 res；
层序遍历：当 queue 为空时跳出；
1. 节点出队，记为 node；
2. 若 node 不为空：① 打印字符串 node.val，② 将左、右子节点加入 queue；
3. 否则（若 node 为空）：打印字符串 "null"；
返回值：拼接列表，用 ',' 隔开，首尾添加中括号；

时间复杂度：O(N)，空间复杂度：O(N)。

反序列化 Deserialize：

利用队列按层构建二叉树，借助一个指针 i 指向节点 node 的左、右子节点，每构建一个 node 的左、右子节点，指针 i 就向右移动 $1$ 位。

算法流程：

特例处理：若 data 为空，直接返回 null；
初始化：序列化列表 vals（先去掉首尾中括号，再用逗号隔开），指针 i = 1，根节点 root（值为 vals[0]），队列 queue（包含 root）；
按层构建：当 queue 为空时跳出；
1. 节点出队，记为 node；
2. 构建 node 的左子节点：node.left 的值为 vals[i]，并将 node.left 入队；
3. 执行 i += 1；
4. 构建 node 的右子节点：node.right 的值为 vals[i]，并将 node.right 入队；
5. 执行 i += 1；
返回值：返回根节点 root 即可；

时间复杂度：O(N)，空间复杂度：O(N)。

public class Codec {
    public String serialize(TreeNode root) {
        if(root == null) return "[]";
        StringBuilder res = new StringBuilder("[");
        Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }};
        while(!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if(node != null) {
                res.append(node.val + ",");
                queue.add(node.left);
                queue.add(node.right);
            }
            else res.append("null,");
        }
        res.deleteCharAt(res.length() - 1);
        res.append("]");
        return res.toString();
    }

    public TreeNode deserialize(String data) {
        if(data.equals("[]")) return null;
        String[] vals = data.substring(1, data.length() - 1).split(",");
        TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
        Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }};
        int i = 1;
        while(!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if(!vals[i].equals("null")) {
                node.left = new TreeNode(Integer.parseInt(vals[i]));
                queue.add(node.left);
            }
            i++;
            if(!vals[i].equals("null")) {
                node.right = new TreeNode(Integer.parseInt(vals[i]));
                queue.add(node.right);
            }
            i++;
        }
        return root;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/997ebc/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

此外，评论区里有人说到：“res.append(node.val + ","); 这个点可以优化成 res.append(node.val).append(",");。因为拼接字符串可能增大消耗。”试了一下确实如此。

剑指 Offer 38. 字符串的排列

难度：中等

根据字符串排列的特点，考虑深度优先搜索所有排列方案。即通过字符交换，先固定第 1 位字符（n 种情况）、再固定第 2 位字符（n−1 种情况）、... 、最后固定第 n 位字符（1 种情况）。

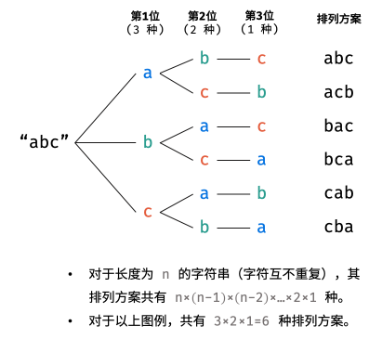
当字符串存在重复字符时，排列方案中也存在重复的排列方案。为排除重复方案，需在固定某位字符时，保证“每种字符只在此位固定一次”，即遇到重复字符时不交换，直接跳过。从 DFS 角度看，此操作称为“剪枝”。

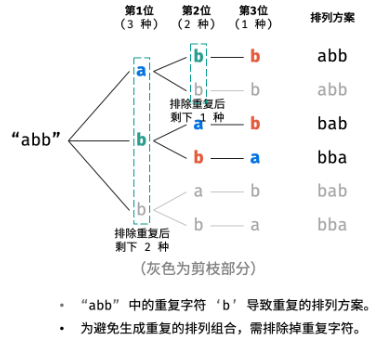
递归解析：

终止条件：当 x = len(c) - 1 时，代表所有位已固定（最后一位只有 1 种情况），则将当前组合 c 转化为字符串并加入 res，并返回；
递推参数：当前固定位 x；
递推工作：初始化一个 Set，用于排除重复的字符；将第 x 位字符与 i ∈ [x, len(c)] 字符分别交换，并进入下层递归；
1. 剪枝：若 c[i] 在 Set 中，代表其是重复字符，因此“剪枝”；
2. 将 c[i] 加入 Set，以便之后遇到重复字符时剪枝；
3. 固定字符：将字符 c[i] 和 c[x] 交换，即固定 c[i] 为当前位字符；
4. 开启下层递归：调用 dfs(x + 1)，即开始固定第 x + 1 个字符；
5. 还原交换：将字符 c[i] 和 c[x] 交换（还原之前的交换）；

class Solution {
    List<String> res = new LinkedList<>();
    char[] c;
    public String[] permutation(String s) {
        c = s.toCharArray();
        dfs(0);
        return res.toArray(new String[res.size()]);
    }
    void dfs(int x) {
        if(x == c.length - 1) {
            res.add(String.valueOf(c));      // 添加排列方案
            return;
        }
        HashSet<Character> set = new HashSet<>();
        for(int i = x; i < c.length; i++) {
            if(set.contains(c[i])) continue; // 重复，因此剪枝
            set.add(c[i]);
            swap(i, x);                      // 交换，将 c[i] 固定在第 x 位
            dfs(x + 1);                      // 开启固定第 x + 1 位字符
            swap(i, x);                      // 恢复交换
        }
    }
    void swap(int a, int b) {
        char tmp = c[a];
        c[a] = c[b];
        c[b] = tmp;
    }
}

作者：Krahets
链接：https://leetcode.cn/leetbook/read/illustration-of-algorithm/50hah3/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

时间复杂度：O(N!N)（字符串拼接需要 O(N)），空间复杂度：O(N²)（Set 需要 N+(N−1)+...+2+1 = (N+1)N/2）。

posted @ 2022-05-07 12:25 幻梦翱翔阅读(40) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

幻梦翱翔

剑指offer一刷：搜索与回溯算法

剑指 Offer 32 - I. 从上到下打印二叉树

方法一：层序遍历 BFS

剑指 Offer 32 - II. 从上到下打印二叉树 II

方法一：层序遍历 BFS

剑指 Offer 32 - III. 从上到下打印二叉树 III

方法一：层序遍历 + 双端队列

方法二：层序遍历 + 双端队列（奇偶逻辑分离）

方法三：层序遍历 + 倒序

剑指 Offer 26. 树的子结构

方法一：先序遍历 + 包含判断

剑指 Offer 27. 二叉树的镜像

方法一：递归法

方法二：辅助栈（或队列）

剑指 Offer 28. 对称的二叉树

方法一：递归法

剑指 Offer 12. 矩阵中的路径

方法一：深度优先搜索（DFS）+ 剪枝

剑指 Offer 13. 机器人的运动范围

方法一：深度优先遍历 DFS

方法二：广度优先遍历 BFS

剑指 Offer 34. 二叉树中和为某一值的路径

剑指 Offer 36. 二叉搜索树与双向链表

剑指 Offer 54. 二叉搜索树的第 k 大节点

剑指 Offer 55 - I. 二叉树的深度

方法一：后序遍历（DFS）

方法二：层序遍历（BFS）

剑指 Offer 55 - II. 平衡二叉树

方法一：后序遍历 + 剪枝（从底至顶）

方法二：先序遍历 + 判断深度（从顶至底）

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

方法一：迭代

方法二：递归

剑指 Offer 68 - II. 二叉树的最近公共祖先

剑指 Offer 37. 序列化二叉树

剑指 Offer 38. 字符串的排列

公告

Loading

幻梦翱翔

剑指offer一刷：搜索与回溯算法

剑指 Offer 32 - I. 从上到下打印二叉树

方法一：层序遍历 BFS

剑指 Offer 32 - II. 从上到下打印二叉树 II

方法一：层序遍历 BFS

剑指 Offer 32 - III. 从上到下打印二叉树 III

方法一：层序遍历 + 双端队列

方法二：层序遍历 + 双端队列（奇偶逻辑分离）

方法三：层序遍历 + 倒序

剑指 Offer 26. 树的子结构

方法一：先序遍历 + 包含判断

剑指 Offer 27. 二叉树的镜像

方法一：递归法

方法二：辅助栈（或队列）

剑指 Offer 28. 对称的二叉树

方法一：递归法

剑指 Offer 12. 矩阵中的路径

方法一：深度优先搜索（DFS）+ 剪枝

剑指 Offer 13. 机器人的运动范围

方法一：深度优先遍历 DFS

方法二：广度优先遍历 BFS

剑指 Offer 34. 二叉树中和为某一值的路径

剑指 Offer 36. 二叉搜索树与双向链表

剑指 Offer 54. 二叉搜索树的第 k 大节点

剑指 Offer 55 - I. 二叉树的深度

方法一：后序遍历（DFS）

方法二：层序遍历（BFS）

剑指 Offer 55 - II. 平衡二叉树

方法一：后序遍历 + 剪枝 （从底至顶）

方法二：先序遍历 + 判断深度 （从顶至底）

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

方法一：迭代

方法二：递归

剑指 Offer 68 - II. 二叉树的最近公共祖先

剑指 Offer 37. 序列化二叉树

剑指 Offer 38. 字符串的排列

公告

方法一：后序遍历 + 剪枝（从底至顶）

方法二：先序遍历 + 判断深度（从顶至底）